山西省太原市2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-03-27 类型:期中考试
一、选择题
-
1. 若 = =2(b+d≠0),则 的值为( )A、1 B、2 C、 D、42. 将方程(x+1)(2x-3)=1化成“ax2+bx+c=0”的形式,当a=2时,则b,c的值分别为( )A、
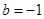 ,
, 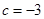 B、
B、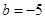 ,
, 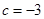 C、
C、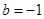 ,
, 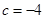 D、
D、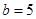 ,
, 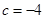 3. 矩形、菱形、正方形都具有的性质是( ).A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角4. 如图,一组互相平行的直线a,b,c分别与直线l1 , 12交于点A,B,C,D,E,F,直线11 , l2交于点O,则下列各式不正确的是( )
3. 矩形、菱形、正方形都具有的性质是( ).A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角4. 如图,一组互相平行的直线a,b,c分别与直线l1 , 12交于点A,B,C,D,E,F,直线11 , l2交于点O,则下列各式不正确的是( )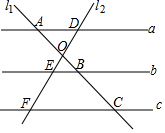 A、
A、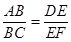 B、
B、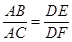 C、
C、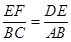 D、
D、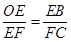 5. 一元二次方程x2+6x+9=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数偎 C、只有一个实数根 D、没有实数根6. 小明要用如图的两个转盘做“配紫色”游戏,每个转盘均被等分成若干个扇形,他同时转动两个转盘,停止时指针所指的颜色恰好配成紫色的概率为( )
5. 一元二次方程x2+6x+9=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数偎 C、只有一个实数根 D、没有实数根6. 小明要用如图的两个转盘做“配紫色”游戏,每个转盘均被等分成若干个扇形,他同时转动两个转盘,停止时指针所指的颜色恰好配成紫色的概率为( ) A、
A、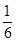 B、
C、
B、
C、 D、
7. 用配方法解方程x2-8x+5=0,将其化为(x+a)2=b的形式,正确的是( )A、
D、
7. 用配方法解方程x2-8x+5=0,将其化为(x+a)2=b的形式,正确的是( )A、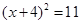 B、
B、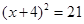 C、
C、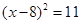 D、
D、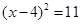 8. 如图,△ABC中,点P是AB边上的一点,过点P作PD∥BC,PE∥AC,分别交AC,BC于点D,E,连按CP.若四边形CDPE是菱形,则线段CP应满足的条件是( )
8. 如图,△ABC中,点P是AB边上的一点,过点P作PD∥BC,PE∥AC,分别交AC,BC于点D,E,连按CP.若四边形CDPE是菱形,则线段CP应满足的条件是( )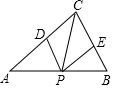 A、 CP平分
A、 CP平分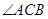 B、
B、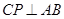 C、CP是AB边上的中线
D、
C、CP是AB边上的中线
D、 9. 为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )
9. 为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( ) A、
A、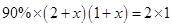 B、
B、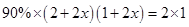 C、
C、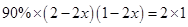 D、
D、 10. 如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )
10. 如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )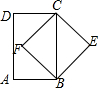 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
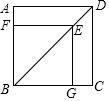
11. 一元二次方程x2+3x=0的解是 .12. 经过某十字路口的行人,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两人经过该路口,则恰好有一人直行,另一人左拐的概率为 .13. 如图,正方形ABCD中,点E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为点F,G,则正方形FBGE与正方形ABCD的相似比为 .
 14. 如图,正方形ABCD中,AB=2,对角线AC,BD相交于点O,将△OBC绕点B逆时针旋转得到△O′BC′,当射线O′C′经过点D时,线段DC′的长为 .
14. 如图,正方形ABCD中,AB=2,对角线AC,BD相交于点O,将△OBC绕点B逆时针旋转得到△O′BC′,当射线O′C′经过点D时,线段DC′的长为 .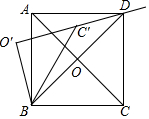 15. 如图,在菱形ABCD中,AB=4,AE⊥BC于点E,点F,G分别是AB,AD的中点,连接EF,FG,若∠EFG=90°,则FG的长为 .
15. 如图,在菱形ABCD中,AB=4,AE⊥BC于点E,点F,G分别是AB,AD的中点,连接EF,FG,若∠EFG=90°,则FG的长为 .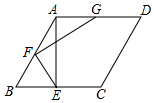
三、计算题
-
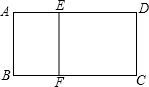
16. 解下列方程:(1)、x2-6x+3=0;(2)、3x(x-2)=2(x-2).17. 如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
四、解答题
-
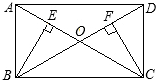
18. 已知,如图,矩形ABCD中,AC与BD相交于点O,BE⊥AC于E,CF⊥BD于F.
求证:BE=CF.
 19. 太原是一座具有4700多年历史、2500年建城史的历史古都,系有“锦绣太原城”的美誉,在“我可爱的家乡”主题班会中,主持人准备了“晋祠园林”、“崇山大佛”、“龙山石窟”、“凌霄双塔”这四处景点的照片各一张,并将它们背面朝上放置(照片背面完全相同),甲同学从中随机抽取一张,不放回,乙再从剩下的照片中随机抽取一张,若要根据抽取的照片作相关景点介绍,求甲、乙两人中恰好有一人介绍“晋祠园林”的概率.(提示:可用照片序号列表或画树状图)
19. 太原是一座具有4700多年历史、2500年建城史的历史古都,系有“锦绣太原城”的美誉,在“我可爱的家乡”主题班会中,主持人准备了“晋祠园林”、“崇山大佛”、“龙山石窟”、“凌霄双塔”这四处景点的照片各一张,并将它们背面朝上放置(照片背面完全相同),甲同学从中随机抽取一张,不放回,乙再从剩下的照片中随机抽取一张,若要根据抽取的照片作相关景点介绍,求甲、乙两人中恰好有一人介绍“晋祠园林”的概率.(提示:可用照片序号列表或画树状图) 20. “早黑宝”是我省农科院研制的优质新品种,在我省被广泛种植.清徐县某葡萄种植基地2016年种植“早黑宝”100亩,到2018年“早黑宝”的种植面积达到225亩.
20. “早黑宝”是我省农科院研制的优质新品种,在我省被广泛种植.清徐县某葡萄种植基地2016年种植“早黑宝”100亩,到2018年“早黑宝”的种植面积达到225亩. (1)、求该基地这两年“早黑宝”种植面积的平均增长率;(2)、市场调查发现,当“早黑宝”售价为20元/千克时,每天能售出200千克,售价每降低1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1800元,则售价应降低多少元?21. 如图,在△ABC中,点D,E,F分别在AB,AC,BC边上,若四边形DEFB为菱形,且AB=8,BC=12,求菱形DEFB的边长.
(1)、求该基地这两年“早黑宝”种植面积的平均增长率;(2)、市场调查发现,当“早黑宝”售价为20元/千克时,每天能售出200千克,售价每降低1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1800元,则售价应降低多少元?21. 如图,在△ABC中,点D,E,F分别在AB,AC,BC边上,若四边形DEFB为菱形,且AB=8,BC=12,求菱形DEFB的边长.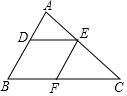 22. 已知:如图,菱形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,且BE=BF=DH=DG.
22. 已知:如图,菱形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,且BE=BF=DH=DG.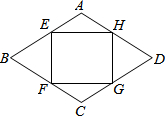 (1)、求证:四边形EFGH是矩形;(2)、已知∠B=60°,AB=6.
(1)、求证:四边形EFGH是矩形;(2)、已知∠B=60°,AB=6.请从A,B两题中任选一题作答,我选择 ▲ 题.
A题:当点E是AB的中点时,矩形EFGH的面积是 .
B题:当BE=时,矩形EFGH的面积是8 .
23. 综合与实践问题情境:正方形折叠中的数学
已知正方形纸片ABCD中,AB=4,点E是AB边上的一点,点G是CE的中点,将正方形纸片沿CE所在直线折叠,点B的对应点为点B′.
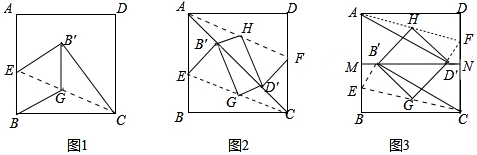 (1)、如图1,当∠BCE=30°时,连接BG,B′G,求证:四边形BEB′G是菱形;(2)、深入探究:
(1)、如图1,当∠BCE=30°时,连接BG,B′G,求证:四边形BEB′G是菱形;(2)、深入探究:在CD边上取点F,使DF=BE,点H是AF的中点,再将正方形纸片ABCD沿AF所在直线折叠,点D的对应点为D′,顺次连接B′,G,D′,H,B',得到四边形B′GD′H.
请你从A,B两题中任选一题作答,我选择 ▲ 题.
A题:如图2,当点B',D′均落在对角线AC上时,
①判断B′G与D′H的数量关系与位置关系,并说明理由;
②直写出此时点H,G之间的距离.
B题:如图3,点M是AB的中点,MN∥BC交CD于点N,当点B',D′均落在MN上时,
①判断B′G与D′H的数量关系与位置关系,并说明理由;
②直接写出此时点H,G之间的距离.