黑龙江省哈尔滨九十五中2018-2019学年八年级上学期数学期中考试试卷(五四学制)
试卷更新日期:2019-03-27 类型:期中考试
一、选择题
-
1. 已知点Q与点P(3,2)关于x轴对称,那么点Q的坐标为( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、
2. 下列计算正确的是( )A、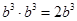 B、
B、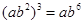 C、
C、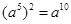 D、
D、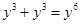 3. 下列四个图形中,不是轴对称图形的是( )A、
3. 下列四个图形中,不是轴对称图形的是( )A、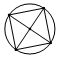 B、
B、 C、
C、 D、
D、 4. 如图:DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为( )厘米.
4. 如图:DE是△ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则△EBC的周长为( )厘米. A、16 B、18 C、26 D、285. 已知:△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是( )
A、16 B、18 C、26 D、285. 已知:△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是( )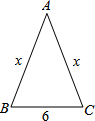 A、
A、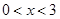 B、
B、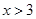 C、
C、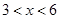 D、
D、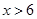 6. 下列命题中的假命题是( )A、等腰直角三角形是直角三角形 B、等边三角形是等腰三角形 C、等腰三角形是锐角三角形 D、等边三角形是锐角三角形7. 如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )
6. 下列命题中的假命题是( )A、等腰直角三角形是直角三角形 B、等边三角形是等腰三角形 C、等腰三角形是锐角三角形 D、等边三角形是锐角三角形7. 如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )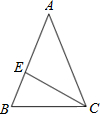 A、
A、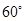 B、
B、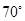 C、
C、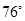 D、
D、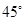 8. 如图所示,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F,则∠DFC的度数为( )
8. 如图所示,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F,则∠DFC的度数为( ) A、
A、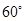 B、
B、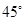 C、
C、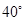 D、
D、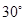 9. 已知一个等腰三角形有两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )
9. 已知一个等腰三角形有两内角的度数之比为1:4,则这个等腰三角形顶角的度数为( )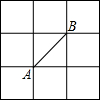 A、
A、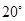 B、
B、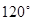 C、
C、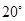 或
或 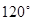 D、
D、 10. 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
10. 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )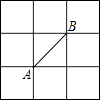 A、6 个 B、7 个 C、8 个 D、9个
A、6 个 B、7 个 C、8 个 D、9个二、填空题
-
11. 若2x-4=8,则x= .12. 已知xa=3,xb=4,则xa+b= .13. 计算:(-3x3)2•xy2=14. 在△ABC中,已知AB=7,BC=6,∠B=30°,那么S△ABC= .15. 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O,与AB,AC相交于点M、N,且MN∥BC,AB=7,AC=9,△ANM的周长是
 16. 如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为°.
16. 如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为°.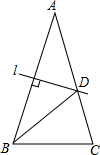 17. 如图所示,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PD=3,则OC的长为
17. 如图所示,∠AOB=30°,P为∠AOB平分线上一点,PC∥OA交OB于点C,PD⊥OA于点D,若PD=3,则OC的长为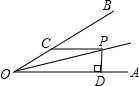 18. 等腰三角形一腰上的高与另一边的夹角为40°,则这个等腰三角形顶角的度数为 .19. 如图,在△ABC中,AB=AC,D、E分别是边BC、AC上一点,且AD=AE,∠BAD=74°,则∠CDE的度数为 .
18. 等腰三角形一腰上的高与另一边的夹角为40°,则这个等腰三角形顶角的度数为 .19. 如图,在△ABC中,AB=AC,D、E分别是边BC、AC上一点,且AD=AE,∠BAD=74°,则∠CDE的度数为 . 20. 如图,△ABC中,AB=BC,∠ABC=120°,E是线段AC上一点,连接BE并延长至D,连接CD,若∠BCD=120°,AB=2CD,AE=7,则线段CE长为 .
20. 如图,△ABC中,AB=BC,∠ABC=120°,E是线段AC上一点,连接BE并延长至D,连接CD,若∠BCD=120°,AB=2CD,AE=7,则线段CE长为 .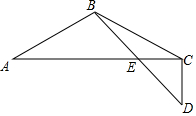
三、计算题
-
21. 先化简,再求值:x2(x-1)-x(x2+x-1),其中x=7.
四、解答题
-
22. 计算(1)、x•(-x)2(-x)3(2)、2(x2)3+3(-x3)223. △ABC在平面直角坐标系中的位置如图.A、B、C三点在格点上.
 (1)、作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标 ▲ ;(2)、在y轴上找点D,使得AD+BD最小,作出点D并写出点D的坐标 ▲ .24.(1)、计算:-82018×(-0.125)2018(2)、已知am=6,an=2,求a2m+3n的值.25. 如图1,等边三角形ABC中,点D为AC中点,延长BC至E,使CE=CD;连接ED并延长交AB于点F.
(1)、作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标 ▲ ;(2)、在y轴上找点D,使得AD+BD最小,作出点D并写出点D的坐标 ▲ .24.(1)、计算:-82018×(-0.125)2018(2)、已知am=6,an=2,求a2m+3n的值.25. 如图1,等边三角形ABC中,点D为AC中点,延长BC至E,使CE=CD;连接ED并延长交AB于点F.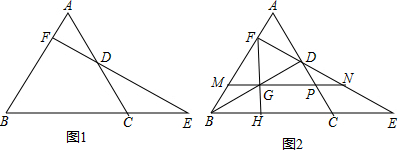 (1)、求证:BF=3AF;(2)、如图2,连接BD,过点F作FH⊥BC,垂足为H,交BD于点G,过点G作BE的平行线,分别交AB、AC、FE于点M、P、N;在不添加任何辅助线的情况下,请直接写出图2中与线段BM相等的所有线段.26. 如图,△ABC为等边三角形.点D,点E为直线AC和BC上的动点.
(1)、求证:BF=3AF;(2)、如图2,连接BD,过点F作FH⊥BC,垂足为H,交BD于点G,过点G作BE的平行线,分别交AB、AC、FE于点M、P、N;在不添加任何辅助线的情况下,请直接写出图2中与线段BM相等的所有线段.26. 如图,△ABC为等边三角形.点D,点E为直线AC和BC上的动点.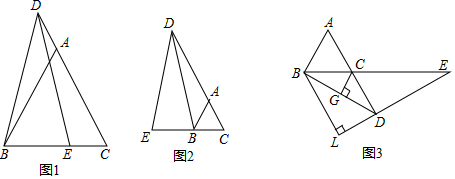 (1)、如图1所示,点D为CA延长线上一点,点E为BC上一点时,连结DB,DE.且DB=DE,求证:AD+BE=AB;(2)、如图2所示,当点E为CB延长线上一点时,DB=DE,直接写出AD,BE,AB之间的关系 .(3)、如图3所示,当点D在AC的延长线上时,点E在BC的延长线上时,DB=DE,过点C作CG⊥DB于点G,过点B作BL⊥ED延长线于点.且 = ,BE=14,求AD的长.27. 如图,△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上
(1)、如图1所示,点D为CA延长线上一点,点E为BC上一点时,连结DB,DE.且DB=DE,求证:AD+BE=AB;(2)、如图2所示,当点E为CB延长线上一点时,DB=DE,直接写出AD,BE,AB之间的关系 .(3)、如图3所示,当点D在AC的延长线上时,点E在BC的延长线上时,DB=DE,过点C作CG⊥DB于点G,过点B作BL⊥ED延长线于点.且 = ,BE=14,求AD的长.27. 如图,△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一锐角顶点B在y轴上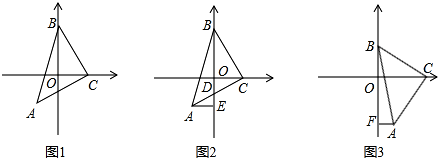 (1)、如图1,若点C的坐标是(2,0),点A的坐标是(-2,-2),求B点的坐标;(2)、如图2,若y轴恰好平分∠ABC,AC与y轴交与点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由(3)、如图3,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,猜想OC、AF、OB之间的关系,并证明你的结论.
(1)、如图1,若点C的坐标是(2,0),点A的坐标是(-2,-2),求B点的坐标;(2)、如图2,若y轴恰好平分∠ABC,AC与y轴交与点D,过点A作AE⊥y轴于E,问BD与AE有怎样的数量关系,并说明理由(3)、如图3,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,猜想OC、AF、OB之间的关系,并证明你的结论.
-