河北省保定市莲池区二中分校2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-03-27 类型:期中考试
一、选择题
-
1. 用直接开平方法解下列一元二次方程,其中无解的方程为( )A、
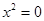 B、
B、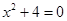 C、
D、
C、
D、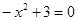 2. 菱形具有而一般平行四边形不具有的性质是( )A、对角线相等 B、对边相等 C、对角线互相平分 D、对角线互相垂直3. 如果两个相似多边形的面积比是4:9,那么它们的周长比是( )A、4:9 B、2:3 C、
2. 菱形具有而一般平行四边形不具有的性质是( )A、对角线相等 B、对边相等 C、对角线互相平分 D、对角线互相垂直3. 如果两个相似多边形的面积比是4:9,那么它们的周长比是( )A、4:9 B、2:3 C、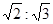 D、16:81
4. 根据下列表格中关于x的代数式 的值与x的对应值,那么你认为方程 ( ≠0, 、b、c为常数)的一个解最接近于下面的( )
D、16:81
4. 根据下列表格中关于x的代数式 的值与x的对应值,那么你认为方程 ( ≠0, 、b、c为常数)的一个解最接近于下面的( )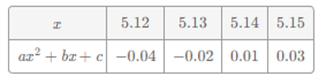 A、5.12 B、5.13 C、5.14 D、5.155. 如图,在平行四边形ABCD中,AC,BD是它的两条对角线,下列条件中,能判断这个平行四边形是矩形的是( )
A、5.12 B、5.13 C、5.14 D、5.155. 如图,在平行四边形ABCD中,AC,BD是它的两条对角线,下列条件中,能判断这个平行四边形是矩形的是( )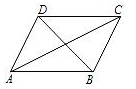 A、∠BAC=∠ACB B、∠BAC=∠ACD C、∠BAC=∠DAC D、∠BAC=∠ABD6. 下列说法正确的是( )A、两个矩形一定相似 B、两个菱形一定相似 C、两个等腰三角形一定相似 D、两个等边三角形一定相似7. 如图,为测量学校旗杆的高度,小东用长为3.2米的竹竿作测量工具,移动竹竿,使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8米,与旗杆相距22米,则旗杆的高度为( )米。
A、∠BAC=∠ACB B、∠BAC=∠ACD C、∠BAC=∠DAC D、∠BAC=∠ABD6. 下列说法正确的是( )A、两个矩形一定相似 B、两个菱形一定相似 C、两个等腰三角形一定相似 D、两个等边三角形一定相似7. 如图,为测量学校旗杆的高度,小东用长为3.2米的竹竿作测量工具,移动竹竿,使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8米,与旗杆相距22米,则旗杆的高度为( )米。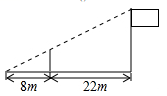 A、8.8 B、10 C、12 D、148. 点C是线段AB的黄金分割点,且AB=6cm,则BC的长为( )cmA、
A、8.8 B、10 C、12 D、148. 点C是线段AB的黄金分割点,且AB=6cm,则BC的长为( )cmA、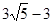 B、
B、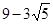 C、
C、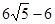 或
或 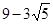 D、
D、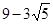 或
或 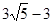 9. 某商店3月份的营业额为15万元,4月份的营业额比3月份的营业额减少10%;商店经过加强管理,实施各种措施,使得5、6月份的营业额连续增长,6月份的营业额达到了20万元;设5、6月份的营业额的平均增长率为x,依题意可列方程为( )A、
9. 某商店3月份的营业额为15万元,4月份的营业额比3月份的营业额减少10%;商店经过加强管理,实施各种措施,使得5、6月份的营业额连续增长,6月份的营业额达到了20万元;设5、6月份的营业额的平均增长率为x,依题意可列方程为( )A、 B、
B、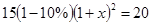 C、
C、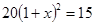 D、
D、 10. 若关于x的一元二次方程 的解是 ,(a,b,m均为常数,a≠0),则方程 的解是( )A、
10. 若关于x的一元二次方程 的解是 ,(a,b,m均为常数,a≠0),则方程 的解是( )A、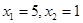 B、
B、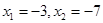 C、
C、 D、
D、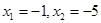 11. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
11. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )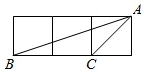 A、
A、 B、
B、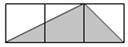 C、
C、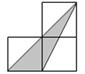 D、
D、 12. 如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
12. 如图,在长为8cm、宽为4cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
A、2cm2 B、4cm2 C、8cm2 D、16cm213. 已知点(k,b)是平面直角坐标系第二象限内的点,则一元二次方程 根的存在情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定14. 关于x的一元二次方程 有实根,则d的最大值为( )A、3 B、4 C、5 D、615. 已知线段a、b、c的长度分别为a=1、b=2、c=3,如果线段d和已知的三个线段是成比例线段,那么线段d的长度等于( )A、6 B、 C、 D、以上三个答案都正确16. 若△ABC的每条边长增加各自的10%得△A'B'C' , 则∠B'的度数与其对应角∠B的度数相比( )
A、增加了10% B、减少了10% C、增加了(1+10%) D、没有变化二、填空题
-
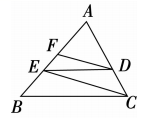
17. 已知实数x,y,z满足 ,则 的值为。18. 如图,在△ABC中,点D为AC上一点,且线段CD与AD之比为1:2,过点D作DE∥BC交AB于点E,连接CE,过点D作DF∥CE,交AB于点F,那么线段EF与EB之比等于。
 19. 如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,BE:ED=1:2,AD=6,则AE的长度为。
19. 如图,在矩形ABCD中,对角线AC,BD交于点O,AE⊥BD于点E,BE:ED=1:2,AD=6,则AE的长度为。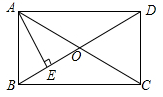 20. 如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,CE,DF交于点O,下面结论:(1)∠DOC=90°,(2)OC=OE,(3)S△ODC=S四边形BEOF。其中正确的有(只填写序号)
20. 如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,CE,DF交于点O,下面结论:(1)∠DOC=90°,(2)OC=OE,(3)S△ODC=S四边形BEOF。其中正确的有(只填写序号)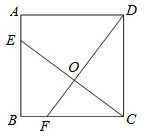
三、解答题
-
21. 解下列方程(1)、 (利用配方法)(2)、 (利用公式法)(3)、 (利用因式分解法)(4)、22. 已知关于x的方程 (其中m为实数)(1)、当m时,已知方程为一元一次方程;(2)、当m时,已知方程为一元二次方程;(3)、若已知方程有实数根,求m的取值范围。23. 已知:在一个不透明的口袋中装有3个红球和一个白球,它们除了颜色外其他都相同。(1)、若从这个口袋中随机地取出1个球,则“取出的球恰好是白球”的概率是;(2)、若从这个口袋中随机地一次性取出2个球,再问问先用树状图或者列表的方法得到所有的结果,然后再求“取出的2个球恰好都是红球”的概率是多少?(3)、若往这个口袋中又加入了与袋中红球一样的若干个红球,在搅匀袋子之后,进行下面随机试验:随机地抽取1个球,记录它的颜色后又放回口袋中,......,我们如此很多次重复做这个试验后发现,取出红球的频率一直稳定在95%附近,那么请你求一下大约又加入了多少个红球?24. 如图,将一张平行四边形纸片ABCD沿着线段EF折叠(点E、F分别在AB边和BC边上),使得点C落在点A处,点D落在点G处。
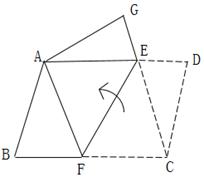 (1)、如果连接EC,那么线段GE与EC在同一条直线上吗?为什么?(2)、试判断四边形AFCE的形状,并说明你是怎样判断的?25. 阅读下面方法,解答后面的问题:
(1)、如果连接EC,那么线段GE与EC在同一条直线上吗?为什么?(2)、试判断四边形AFCE的形状,并说明你是怎样判断的?25. 阅读下面方法,解答后面的问题:【阅读理解】我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用。
例题:已知x可取任意实数,试求二次三项式 的取值范围。
解:
∵x取任何实数,总有 ,∴ 。
因此,无论x取任何实数, 的值总是不小于-4的实数。
特别的,当x=3时, 有最小值-4
(1)、【应用1】:已知x可取任何实数,则二次三项式 的最值情况是( )A、有最大值-10 B、有最小值-10 C、有最大值-7 D、有最小值-7(2)、【应用2】:某品牌服装进货价为每件50元,商家在销售中发现:当以每件90元销售时,平均每天可售出20件,为了扩大销售量,增加盈利,商家决定采取适当的降价措施。①将市场调查发现:如果每件服装降价1元,那么平均每天那就可多售出2件,要想平均每天销售这种服装盈利为1200元,我们设降价x元,根据题意列方程得( )
A. B.
C. D.
②请利用上面【阅读理解】提供的方法解决下面问题:
这家服装专柜为了获得每天的最大盈利,每件服装需要降价多少元?每天的最大盈利又是多少元?
26. 如图1,在四边形ABCD中,AD∥BC,∠C=90°,BC=16cm,DC=12cm,AD=21cm,点P以2cm/s的速度沿DA边由点D向点A运动,同时点Q以1cm/s的速度沿CB边由点C向点B运动,而且当其中一点停止运动时另一点也停止运动。设运功时间为t(s)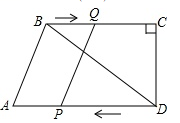 (1)、用含t的代数式表示下面线段的长度:
(1)、用含t的代数式表示下面线段的长度:①CQ=cm ②PD=cm
③BQ=cm ④AP=cm
(2)、当t为s时,PQ∥AB(3)、是否存在某一时刻t,使得PQ⊥BD?若存在,求出t值;若不存在,请说明理由。