河北省保定市定兴二中三校区联考2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-03-27 类型:期中考试
一、选择题
-
1. 方程x2=5x的根是( )A、x=5 B、x=0 C、x1=0,x2=5 D、x1=0,x2=-52. 已知2x=3y,则下列比例式成立的是( )A、
 B、
B、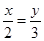 C、
C、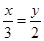 D、
D、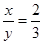 3. 正方形网格中,∠AOB如图放置,则tan∠AOB的值为( )
3. 正方形网格中,∠AOB如图放置,则tan∠AOB的值为( )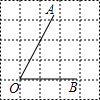 A、2 B、
A、2 B、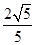 C、
D、
4. 在△ABC中,DE∥BC,分别交边AB、AC于点D、E,AD:BD=1:2,那么△ADE与△ABC面积的比为( )
C、
D、
4. 在△ABC中,DE∥BC,分别交边AB、AC于点D、E,AD:BD=1:2,那么△ADE与△ABC面积的比为( ) A、1:2 B、1:4 C、1:3 D、1:95. 用配方法解一元二次方程x2+8x+7=0,则方程可化为( )A、
A、1:2 B、1:4 C、1:3 D、1:95. 用配方法解一元二次方程x2+8x+7=0,则方程可化为( )A、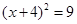 B、
B、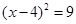 C、
C、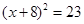 D、
D、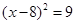 6. 某品牌服装原价800元,连续两次降价x%后售价为512元,下面所列方程中正确的是( )A、
6. 某品牌服装原价800元,连续两次降价x%后售价为512元,下面所列方程中正确的是( )A、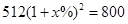 B、
B、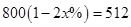 C、
C、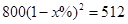 D、
D、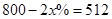 7. 判断一元二次方程x2-2x+1=0的根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根8. 如图,直线l1∥l2∥l3 , 若AB=3,BC=4,则 的值是( )
7. 判断一元二次方程x2-2x+1=0的根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根8. 如图,直线l1∥l2∥l3 , 若AB=3,BC=4,则 的值是( ) A、 B、
A、 B、 C、
D、
9. 在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )
C、
D、
9. 在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )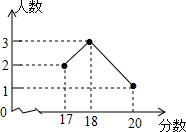 A、18,18,1 B、18,
A、18,18,1 B、18,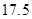 ,3
C、18,18,3
D、18,
,3
C、18,18,3
D、18, 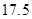 ,1
10. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
,1
10. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )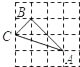 A、
A、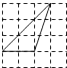 B、
B、 C、
C、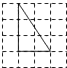 D、
D、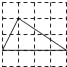 11. 下列命题中真命题的个数是( )
11. 下列命题中真命题的个数是( )①两个相似三角形的面积比等于相似比的平方;
②两个相似三角形对应高的比等于相似比;
③已知△ABC及位似中心O,能够作一个且只能作一个三角形,使位似比为0.5.
A、0 B、1 C、2 D、312. 小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )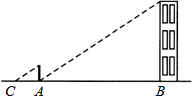 A、10米 B、12米 C、15米 D、
A、10米 B、12米 C、15米 D、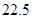 米
13. 如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )
米
13. 如图,在平面直角坐标系中,以原点O为位似中心,将△ABO扩大到原来的2倍,得到△A′B′O.若点A的坐标是(1,2),则点A′的坐标是( )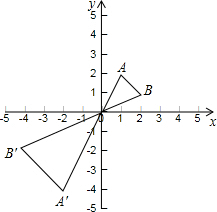 A、
A、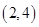 B、
B、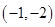 C、
C、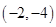 D、
D、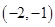 14. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
14. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )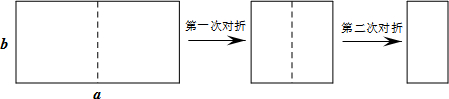 A、
A、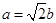 B、
B、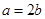 C、
C、 D、
15. 如图,在直角三角形ABC中(∠C=90°),放置边长分别为3,4,x的三个正方形,则x的值为( )
D、
15. 如图,在直角三角形ABC中(∠C=90°),放置边长分别为3,4,x的三个正方形,则x的值为( )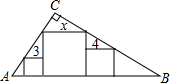 A、5 B、6 C、7 D、1216. 关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正.给出三个结论:①这两个方程的根都是负根;② (m-1)2+(n-1)2≥2;③-1≤2m-2n≤1.其中正确结论的个数是( )
A、5 B、6 C、7 D、1216. 关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正.给出三个结论:①这两个方程的根都是负根;② (m-1)2+(n-1)2≥2;③-1≤2m-2n≤1.其中正确结论的个数是( )
A、0个 B、1个 C、2个 D、3个二、填空题
-
17. 已知: ,则 的值为 .18. 若|b-1|+ =0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
19. 如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE.若BE=9,BC=12,则cosC= . 20. 如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1 , △B3D2C2的面积为S2 , …,△Bn+1DnCn的面积为Sn , 则S1= ,Sn= (用含n的式子表示).
20. 如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1 , △B3D2C2的面积为S2 , …,△Bn+1DnCn的面积为Sn , 则S1= ,Sn= (用含n的式子表示).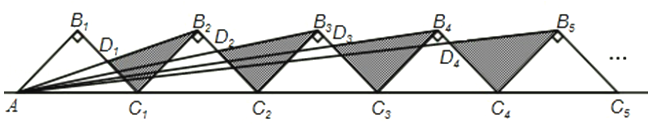
三、计算题
-
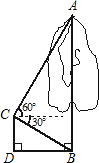
21. 为申办2010年冬奥会,须改变哈尔滨市的交通状况.在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30度.问:距离B点8米远的保护物是否在危险区内?
四、解答题
-
22.(1)、x2-2x-1=0(2)、3x(x-1)=2(x-1)23. 小明、小兵参加某体育项目训练,教练对他们近期的8次测试成绩进行了统计,如折线图所示:
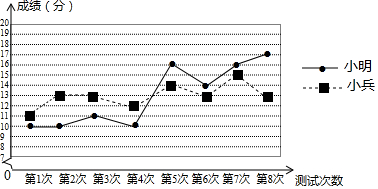 (1)、根据折线图中提供的数据填写下表:
(1)、根据折线图中提供的数据填写下表:平均数(分)
众数(分)
中位数(分)
最高成绩(分)
方差(分2)
小明
13
10
17
8.25
小兵
13
13
1.25
(2)、教练欲从两人中选出一人参加市中学生运动会,根据上述统计情况填空:从平均数的角度分析,二人的实力;
从众数的角度分析,的成绩更好;
从最高成绩分析,的成绩更好;
从方差的角度分析,的成绩更稳定;
综合以上四个方面的分析,教练应选择参加比赛.
24. 某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).项目
第一次锻炼
第二次锻炼
步数(步)
10000
① ▲
平均步长(米/步)
0.6
② ▲
距离(米)
6000
7020
注:步数×平均步长=距离.
(1)、根据题意完成表格填空;(2)、求x;(3)、王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.25. 在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.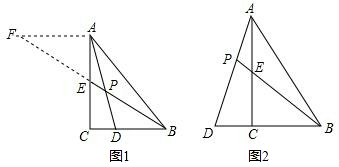
发现:如图1,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,易得 的值为 ▲ .
解决问题:如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC=1:2.求 的值:
应用:若CD=2,AC=6,则BP= ▲ .
26. 如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE--EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0). (1)、当t=1时,KE= , EN=;(2)、当t为何值时,△APM的面积与△MNE的面积相等?(3)、当点K到达点N时,求出t的值;(4)、当t为何值时,△PKB是直角三角形?
(1)、当t=1时,KE= , EN=;(2)、当t为何值时,△APM的面积与△MNE的面积相等?(3)、当点K到达点N时,求出t的值;(4)、当t为何值时,△PKB是直角三角形?
-