四川省遂宁市2018年中考数学试卷
试卷更新日期:2019-03-26 类型:中考真卷
一、单选题
-
1. -2×(-5)的值是( )A、-7 B、7 C、-10 D、102. 下列等式成立的是( )A、x2+3x2=3x4 B、0.00028=2.8×10-3 C、(a3b2)3=a9b6 D、(-a+b)(-a-b)=ab2-a23. 二元一次方程组 的解是( )A、
 B、
B、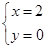 C、
C、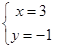 D、
D、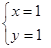 4. 下列说法正确的是( )A、有两条边和一个角对应相等的两个三角形全等 B、正方形既是轴对称图形又是中心对称图形 C、矩形的对角线互相垂直平分 D、六边形的内角和是540°5. 如图,5个完全相同的小正方体组成了一个几何体,则这个几何体的主视图是( )
4. 下列说法正确的是( )A、有两条边和一个角对应相等的两个三角形全等 B、正方形既是轴对称图形又是中心对称图形 C、矩形的对角线互相垂直平分 D、六边形的内角和是540°5. 如图,5个完全相同的小正方体组成了一个几何体,则这个几何体的主视图是( )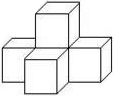 A、
A、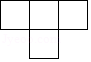 B、
B、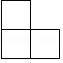 C、
C、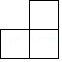 D、
D、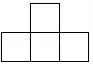 6. 已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是( )A、4π B、8π C、12π D、16π7. 已知一次函数y1=kx+b((k≠0)与反比例函数y2= (m>0)的图象如图所示, 则当y1>y2时, 自变量x满足的条件是( )
6. 已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是( )A、4π B、8π C、12π D、16π7. 已知一次函数y1=kx+b((k≠0)与反比例函数y2= (m>0)的图象如图所示, 则当y1>y2时, 自变量x满足的条件是( )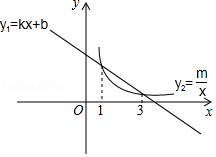 A、1<x<3 B、1≤x≤3 C、x>1 D、x<38. 如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2 ,CD=1,则BE的长是( )
A、1<x<3 B、1≤x≤3 C、x>1 D、x<38. 如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=2 ,CD=1,则BE的长是( )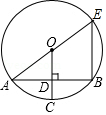 A、5 B、6 C、7 D、89. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是( )
A、5 B、6 C、7 D、89. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是( ) A、
A、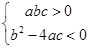 B、
B、 C、
C、 D、
D、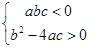 10. 已知如图,在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论:①DE+BF=EF,②BF= ,③AF= ,④S△MEF= 中正确的是( )
10. 已知如图,在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论:①DE+BF=EF,②BF= ,③AF= ,④S△MEF= 中正确的是( )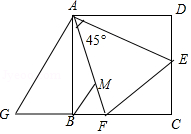 A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
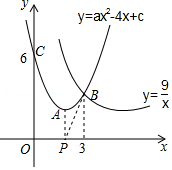
11. 分解因式3a2-3b2= .12. 已知一组数据:12,10,8,15,6,8.则这组数据的中位数是 .13. 已知反比例函数y= (k≠0) 的图象过点(-1,2),则当x>0时,y随x的增大而 .14. A,B两市相距200千米,甲车从A市到B市,乙车从B市到A市,两车同时出发,已知甲车速度比乙车速度快15千米/小时,且甲车比乙车早半小时到达目的地.若设乙车的速度是x千米/小时,则根据题意,可列方程 .15. 如图,已知抛物线y=ax2-4x+c(a≠0)与反比例函数y= 的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为 .
三、解答题
-
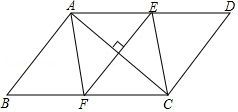
16. 计算: .17. 先化简,再求值 .(其中x=1,y=2)18. 如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
 19. 已知关于x的一元二次方程x2-2x+a=0的两实数根x1 , x2满足x1x2+x1+x2>0,求a的取值范围.20. 如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y= (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD= ,且点B的坐标为(n,-2).
19. 已知关于x的一元二次方程x2-2x+a=0的两实数根x1 , x2满足x1x2+x1+x2>0,求a的取值范围.20. 如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y= (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD= ,且点B的坐标为(n,-2).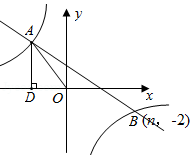 (1)、求一次函数与反比例函数的解析式;(2)、E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.21. 如图,过⊙O外一点P作⊙O的切线PA切⊙O于点A,连接PO并延长,与⊙O交于C、D两点,M是半圆CD的中点,连接AM交CD于点N,连接AC、CM.
(1)、求一次函数与反比例函数的解析式;(2)、E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.21. 如图,过⊙O外一点P作⊙O的切线PA切⊙O于点A,连接PO并延长,与⊙O交于C、D两点,M是半圆CD的中点,连接AM交CD于点N,连接AC、CM.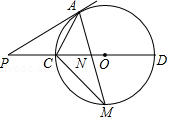 (1)、求证:CM2=MN.MA;(2)、若∠P=30°,PC=2,求CM的长.22. 请阅读以下材料:已知向量 =(x1 , y1), =(x2 , y2)满足下列条件:
(1)、求证:CM2=MN.MA;(2)、若∠P=30°,PC=2,求CM的长.22. 请阅读以下材料:已知向量 =(x1 , y1), =(x2 , y2)满足下列条件:①| |= ,| |=
② (角 的取值范围是0°< <90°);
③
利用上述所给条件解答问题:
如:已知 =(1, ), =(- ,3),求角 的大小;
解:∵| |= = ,
=
∴ =2×2 cos =4 cos
又∵ = ×(- )+ ×3=2
∴4 cos =2 ,
∴cos = ,∴ =60°
角 的值为60°.
请仿照以上解答过程,完成下列问题:
已知 , ,求角 的大小.
23. 学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.
请根据图中信息,解答下列问题:
(1)、求全班学生总人数;(2)、将上面的条形统计图与扇形统计图补充完整;(3)、张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请用画树状图或列表法求出全是B类学生的概率.24. 如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为 的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).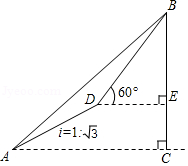 25. 如图, 已知抛物线 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
25. 如图, 已知抛物线 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 . (1)、求抛物线的解析式和A、B两点的坐标;(2)、若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;(3)、若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
(1)、求抛物线的解析式和A、B两点的坐标;(2)、若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;(3)、若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .