宁夏2018年中考数学试卷

试卷更新日期：2019-03-26 类型：中考真卷

进入出卷网下载

一、单选题

1. 计算： $| - \frac{1}{2} | - \sqrt{\frac{1}{4}}$ 的结果是（）

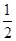A、1 B、 C、0 D、-1

查看试题解析
2. 下列运算正确的是（）

A、(-a)³=a³ B、(a²)³=a⁵ C、a²÷a^-2=1 D、（-2a³）²=4a⁶

查看试题解析
3. 小亮家1月至10月的用电量统计如图所示，这组数据的众数和中位数分别是（）

A、30和 20 B、30和25 C、30和22.5 D、30和17.5

查看试题解析
4. 若2- $\sqrt{3}$ 是方程x²-4x+c=0的一个根，则c的值是（）

A、1 B、3- C、1+ D、2+

查看试题解析
5. 某企业2018年初获利润300万元，到2020年初计划利润达到507万元.设这两年的年利润平均增长率为x.应列方程是（）

A、300（1+x）=507 B、300（1+x）²=507 C、300（1+x）+300（1+x）²=507 D、300+300（1+x）+300（1+x）²=507

查看试题解析
6. 用一个半径为30，圆心角为120°的扇形围成一个圆锥，则这个圆锥的底面半径是（）

A、10 B、20 C、10π D、20π

查看试题解析
7. 将一个矩形纸片按如图所示折叠，若∠1=40°，则∠2的度数是（）

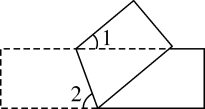A、40° B、50° C、60° D、70°

查看试题解析
8. 如图，一个长方体铁块放置在圆柱形水槽容器内，向容器内按一定的速度均匀注水，60秒后将容器内注满.容器内水面的高度h（cm）与注水时间t（s）之间的函数关系图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 不透明的布袋里有1个黄球、4个红球、5个白球，它们除颜色外其他都相同，那么从布袋中任意摸出一球恰好为红球的概率是.

查看试题解析
10. 已知m+n=12,m-n=2,则m²-n²=.

查看试题解析
11. 反比例函数 $y = \frac{k}{x}$ （k是常数，k≠0）的图象经过点（1,4），那么这个函数图象所在的每个象限内，y的值随x值的增大而.（填“增大”或“减小”）

查看试题解析
12. 已知： $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a - 2 b}{a + 2 b}$ 的值是.

查看试题解析
13. 关于x的方程2x²-3x+c=0 有两个不相等的实数根，则c的取值范围是.

查看试题解析
14. 在平面直角坐标系中，四边形AOBC为矩形，且点C坐标为（8，6），M为BC中点，反比例函数 $y = \frac{k}{x}$ （k是常数，k≠0）的图象经过点M，交AC于点N，则MN的长度是.

查看试题解析
15. 一艘货轮以18 $\sqrt{2}$ ㎞/h的速度在海面上沿正东方向航行，当行驶至A处时，发现它的东南方向有一灯塔B，货轮继续向东航行30分钟后到达C处，发现灯塔B在它的南偏东15°方向，则此时货轮与灯塔B的距离是km.

查看试题解析
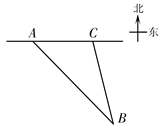16. 如图是各大小型号的纸张长宽关系裁剪对比图，可以看出纸张大小的变化规律：A0纸长度方向对折一半后变为A₁纸；A₁纸长度方向对折一半后变为A₂纸；A₂纸长度方向对折一半后变为A₃纸；A₃纸长度方向对折一半后变为A₄纸……A₄规格的纸是我们日常生活中最常见的，那么有一张A₄的纸可以裁张A8的纸.

查看试题解析

三、解答题

17. 解不等式组： ${\begin{matrix} x - 3 (x - 1) \geq 5 \\ \frac{x - 3}{5} - 1 < \frac{x + 1}{2} \end{matrix}$

查看试题解析
18. 先化简，再求值： $(\frac{1}{x + 3} - \frac{1}{3 - x}) \div \frac{2}{x - 3}$ ；其中， $x = \sqrt{3} - 3$ .

查看试题解析
19. 已知：△ABC三个顶点的坐标分别为A（－2，－2），B（－5，－4），C（－1，－5）.

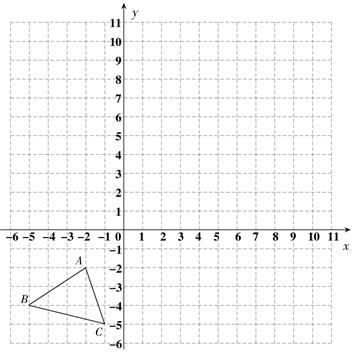
①画出△ABC关于x轴对称的△A₁B₁C₁；

②以点O为位似中心，将△ABC放大为原来的2倍，得到△A₂B₂C₂ ，请在网格中画出△A₂B₂C₂ ，并写出点B₂的坐标.

查看试题解析
20. 某区规定学生每天户外体育活动时间不少于1小时.为了解学生参加户外体育活动的情况，对部分学生每天参加户外体育活动的时间进行了随机抽样调查，并将调查结果绘制成如下的统计表（不完整）.

请根据图表中的信息，解答下列问题：

(1)、写出表中a的值，将频数分布直方图补全；

(2)、该区8000名学生中，每天户外体育活动的时间不足1小时的学生大约有多少名？

(3)、若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名，请用画树状图或列表法求恰好抽到1名男生和1名女生的概率.

查看试题解析
21. 已知点E为正方形ABCD的边AD上一点，连接BE，过点C作CN⊥BE，垂足为M，交AB于点N.

(1)、求证：△ABE≌△BCN；

(2)、若N为AB的中点，求tan∠ABE.

查看试题解析
22. 某工厂计划生产一种创新产品，若生产一件这种产品需A种原料1.2千克、B种原料1千克.已知A种原料每千克的价格比B种原料每千克的价格多10元.

(1)、为使每件产品的成本价不超过34元，那么购入的B种原料每千克的价格最高不超过多少元？

(2)、将这种产品投放市场批发销售一段时间后，为拓展销路又开展了零售业务，每件产品的零售价比批发价多30元.现用10000元通过批发价购买该产品的件数与用16000元通过零售价购买该产品的件数相同，那么这种产品的批发价是多少元？

查看试题解析
23. 已知：AB为⊙O的直径，延长AB到点P，过点P作圆O的切线，切点为C，连接AC，且AC=CP.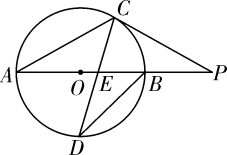

(1)、求∠P的度数；

(2)、若点D是弧AB的中点，连接CD交AB于点E，且DE·DC=20，求⊙O的面积.（π取3.14）

查看试题解析
24. 抛物线 $y = - \frac{1}{3} x^{2} + b x + c$ 经过点A(3 $\sqrt{3}$ ，0) 和点B（0，3），且这个抛物线的对称轴为直线l，顶点为C.

(1)、求抛物线的解析式；

(2)、连接AB、AC、BC，求△ABC的面积.

查看试题解析

25. 空间任意选定一点O，以点O为端点，作三条互相垂直的射线ox、oy、oz.这三条互相垂直的射线分别称作x轴、y轴、z轴，统称为坐标轴，它们的方向分别为ox（水平向前）、oy（水平向右）、oz（竖直向上）方向，这样的坐标系称为空间直角坐标系.

将相邻三个面的面积记为S₁、S₂、S₃ ，且S₁＜S₂＜S₃的小长方体称为单位长方体，现将若干个单位长方体在空间直角坐标系内进行码放，要求码放时将单位长方体S₁所在的面与x轴垂直，S₂所在的面与y轴垂直，S₃所在的面与z轴垂直，如图1所示.

若将x轴方向表示的量称为几何体码放的排数，y轴方向表示的量称为几何体码放的列数，z轴方向表示的量称为几何体码放的层数；如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体，其中这个几何体共码放了1排2列6层，用有序数组记作（1，2，6），如图3的几何体码放了2排3列4层，用有序数组记作（2，3，4）.这样我们就可用每一个有序数组（x，y，z）表示一种几何体的码放方式.

(1)、如图是由若干个单位长方体码放的一个几何体的三视图，写出这种码放方式的有序数组，组成这个几何体的单位长方体的个数为多少个；

(2)、对有序数组性质的理解，下列说法正确的是哪些；（只写序号）

①每一个有序数组（x，y，z）表示一种几何体的码放方式.

②有序数组中x、y、z的乘积就表示几何体中单位长方体的个数.

③有序数组不同，所表示几何体的单位长方体个数不同.

④不同的有序数组所表示的几何体的体积不同.

⑤有序数组中x、y、z每两个乘积的2倍可分别确定几何体表面上S₁、S₂、S₃的个数.

(3)、为了进一步探究有序数组（x，y，z）的几何体的表面积公式S_{（x，y，z）} ，某同学针对若干个单位长方体进行码放，制作了下列表格：

几何体有序数组	单位长方体的个数	表面上面积为 $S_{1}$ 的个数	表面上面积为 $S_{2}$ 的个数	表面上面积为 $S_{3}$ 的个数	表面积
(1，1，1)	1	2	2	2	2S₁+2S₂+2S₃
(1，2，1)	2	4	2	4	4S₁+2S₂+4S₃
(3，1，1)	3	2	6	6	2S₁+6S₂+6S₃
(2，1，2)	4	4	8	4	4S₁+8S₂+4S₃
(1，5，1)	5	10	2	10	10S₁+2S₂+10S₃
(1，2，3)	6	12	6	4	12S₁+6S₂+4S₃
(1，1，7)	7	14	14	2	14S₁+14S₂+2S₃
(2，2，2)	8	8	8	8	8S₁+8S₂+8S₃
…	…	…	…	…	…

根据以上规律，请写出有序数组（x，y，z）的几何体表面积计算公式S_{（x，y，z）}；（用x、y、z、S₁、S₂、S₃表示）

(4)、当S₁=2，S₂=3，S₃=4时，对由12个单位长方体码放的几何体进行打包，为了节约外包装材料，对12个单位长方体码放的几何体表面积最小的规律进行探究，根据探究的结果请写出使几何体表面积最小的有序数组，并用几何体表面积公式求出这个最小面积.（缝隙不计）

查看试题解析

26. 如图：一次函数 $y = - \frac{3}{4} x + 3$ 的图象与坐标轴交于A、B两点，点P是函数 $y = - \frac{3}{4} x + 3$ （0＜x＜4）图象上任意一点，过点P作PM⊥y轴于点M，连接OP.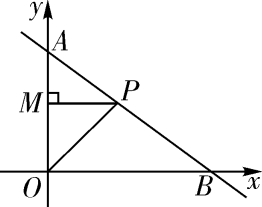

(1)、当AP为何值时，△OPM的面积最大？并求出最大值；

(2)、当△BOP为等腰三角形时，试确定点P的坐标.

查看试题解析