湖南省永州市2018年中考数学试题
试卷更新日期:2019-03-26 类型:中考真卷
一、单选题
-
1. ﹣2018的相反数是( )A、2018 B、﹣2018 C、
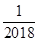 D、
D、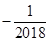 2. 誉为全国第三大露天碑林的“浯溪碑林”,摩崖上铭刻着500多方古今名家碑文,其中悬针篆文具有较高的历史意义和研究价值,下面四个悬针篆文文字明显不是轴对称图形的是( )A、
2. 誉为全国第三大露天碑林的“浯溪碑林”,摩崖上铭刻着500多方古今名家碑文,其中悬针篆文具有较高的历史意义和研究价值,下面四个悬针篆文文字明显不是轴对称图形的是( )A、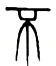 B、
B、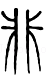 C、
C、 D、
D、 3. 函数y 中自变量x的取值范围是( )A、x≥3 B、x<3 C、x≠3 D、x=34. 如图几何体的主视图是( )
3. 函数y 中自变量x的取值范围是( )A、x≥3 B、x<3 C、x≠3 D、x=34. 如图几何体的主视图是( )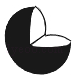 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、m2+2m3=3m5 B、m2•m3=m6 C、(﹣m)3=﹣m3 D、(mn)3=mn36. 已知一组数据45,51,54,52,45,44,则这组数据的众数、中位数分别为( )A、45,48 B、44,45 C、45,51 D、52,537. 下列命题是真命题的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、任意多边形的内角和为360° D、三角形的中位线平行于第三边,并且等于第三边的一半8. 如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为( )
5. 下列运算正确的是( )A、m2+2m3=3m5 B、m2•m3=m6 C、(﹣m)3=﹣m3 D、(mn)3=mn36. 已知一组数据45,51,54,52,45,44,则这组数据的众数、中位数分别为( )A、45,48 B、44,45 C、45,51 D、52,537. 下列命题是真命题的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、任意多边形的内角和为360° D、三角形的中位线平行于第三边,并且等于第三边的一半8. 如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为( ) A、2 B、4 C、6 D、89. 在同一平面直角坐标系中,反比例函数y (b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( )A、
A、2 B、4 C、6 D、89. 在同一平面直角坐标系中,反比例函数y (b≠0)与二次函数y=ax2+bx(a≠0)的图象大致是( )A、 B、
B、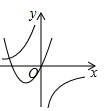 C、
C、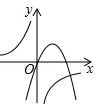 D、
D、 10. 甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A,B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A,B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )A、商贩A的单价大于商贩B的单价 B、商贩A的单价等于商贩B的单价 C、商版A的单价小于商贩B的单价 D、赔钱与商贩A,商贩B的单价无关
10. 甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A,B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A,B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )A、商贩A的单价大于商贩B的单价 B、商贩A的单价等于商贩B的单价 C、商版A的单价小于商贩B的单价 D、赔钱与商贩A,商贩B的单价无关二、填空题
-
11. 截止2017年年底,我国60岁以上老龄人口达2.4亿,占总人口比重达17.3%.将2.4亿用科学记数法表示为 .12. 一副透明的三角板,如图叠放,直角三角板的斜边AB、CE相交于点D,则∠BDC= .
 13. 化简:(1 .14. 在一个不透明的盒子中装有n个球,它们除了颜色之外其它都没有区别,其中含有3个红球,每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.03,那么可以推算出n的值大约是 .15. 如图,在平面直角坐标系中,已知点A(1,1),以点O为旋转中心,将点A逆时针旋转到点B的位置,则 的长为 .
13. 化简:(1 .14. 在一个不透明的盒子中装有n个球,它们除了颜色之外其它都没有区别,其中含有3个红球,每次摸球前,将盒中所有的球摇匀,然后随机摸出一个球,记下颜色后再放回盒中.通过大量重复试验,发现摸到红球的频率稳定在0.03,那么可以推算出n的值大约是 .15. 如图,在平面直角坐标系中,已知点A(1,1),以点O为旋转中心,将点A逆时针旋转到点B的位置,则 的长为 .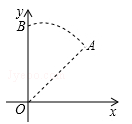 16. 对于任意大于0的实数x、y,满足:log2(x•y)=log2x+log2y,若log22=1,则log216= .17. 现有A、B两个大型储油罐,它们相距2km,计划修建一条笔直的输油管道,使得A、B两个储油罐到输油管道所在直线的距离都为0.5km,输油管道所在直线符合上述要求的设计方案有种.
16. 对于任意大于0的实数x、y,满足:log2(x•y)=log2x+log2y,若log22=1,则log216= .17. 现有A、B两个大型储油罐,它们相距2km,计划修建一条笔直的输油管道,使得A、B两个储油罐到输油管道所在直线的距离都为0.5km,输油管道所在直线符合上述要求的设计方案有种.三、解答题
-
18. 计算:2﹣1 sin60°+|1 |.19. 解不等式组 ,并把解集在数轴上表示出来.20. 永州植物园“清风园”共设11个主题展区.为推进校园文化建设,某校九年级(1)班组织部分学生到“清风园”参观后,开展“我最喜欢的主题展区”投票调查.要求学生从“和文化”、“孝文化”、“德文化”、“理学文化”、“瑶文化”五个展区中选择一项,根据调查结果绘制出了两幅不完整的条形统计图和扇形统计图.结合图中信息,回答下列问题.
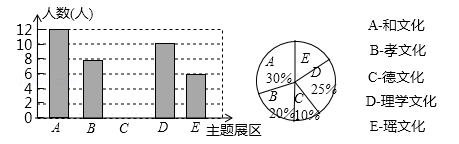 (1)、参观的学生总人数为人;(2)、在扇形统计图中最喜欢“瑶文化”的学生占参观总学生数的百分比为;(3)、补全条形统计图;(4)、从最喜欢“德文化”的学生中随机选两人参加知识抢答赛,最喜欢“德文化”的学生甲被选中的概率为 .21. 如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)、参观的学生总人数为人;(2)、在扇形统计图中最喜欢“瑶文化”的学生占参观总学生数的百分比为;(3)、补全条形统计图;(4)、从最喜欢“德文化”的学生中随机选两人参加知识抢答赛,最喜欢“德文化”的学生甲被选中的概率为 .21. 如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.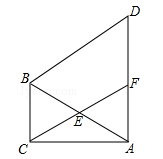 (1)、求证:四边形BCFD为平行四边形;(2)、若AB=6,求平行四边形BCFD的面积.22. 在永州市青少年禁毒教育活动中,某班男生小明与班上同学一起到禁毒教育基地参观,以下是小明和妈妈的对话,请根据对话内容,求小明班上参观禁毒教育基地的男生和女生的人数.
(1)、求证:四边形BCFD为平行四边形;(2)、若AB=6,求平行四边形BCFD的面积.22. 在永州市青少年禁毒教育活动中,某班男生小明与班上同学一起到禁毒教育基地参观,以下是小明和妈妈的对话,请根据对话内容,求小明班上参观禁毒教育基地的男生和女生的人数. 23. 如图,线段AB为⊙O的直径,点C,E在⊙O上, ,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
23. 如图,线段AB为⊙O的直径,点C,E在⊙O上, ,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.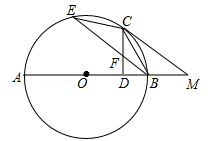 (1)、求证:CF=BF;(2)、若cos∠ABE ,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.24. 如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)、求证:CF=BF;(2)、若cos∠ABE ,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.24. 如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).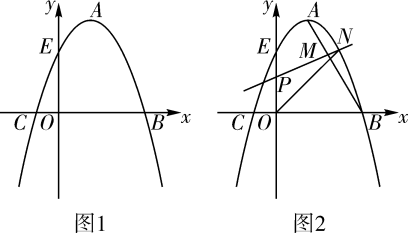 (1)、求抛物线的表达式;(2)、已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.(3)、如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.25. 如图1.在△ABC中,矩形EFGH的一边EF在AB上,顶点G、H分别在BC、AC上,CD是边AB上的高,CD交GH于点I.若CI=4,HI=3,AD .矩形DFGI恰好为正方形.
(1)、求抛物线的表达式;(2)、已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.(3)、如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.25. 如图1.在△ABC中,矩形EFGH的一边EF在AB上,顶点G、H分别在BC、AC上,CD是边AB上的高,CD交GH于点I.若CI=4,HI=3,AD .矩形DFGI恰好为正方形. (1)、求正方形DFGI的边长;(2)、如图2,延长AB至P.使得AC=CP,将矩形EFGH沿BP的方向向右平移,当点G刚好落在CP上时,试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形,为什么?(3)、如图3,连接DG,将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′,正方形DF′G′I′分别与线段DG、DB相交于点M、N,求△MNG′的周长.
(1)、求正方形DFGI的边长;(2)、如图2,延长AB至P.使得AC=CP,将矩形EFGH沿BP的方向向右平移,当点G刚好落在CP上时,试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形,为什么?(3)、如图3,连接DG,将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′,正方形DF′G′I′分别与线段DG、DB相交于点M、N,求△MNG′的周长.