浙江省杭州市滨江区“江浦兴涛”四校2019届九年级12月五科联赛数学试卷
试卷更新日期:2019-03-26 类型:竞赛测试
一、单选题
-
1. 抛掷一枚质地均匀的立方体骰子一次,骰子的六个面上分别标有数字1,2,3,4,5,6,则朝上一面的数字为2的概率是( )A、 B、 C、 D、
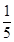 2. 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是( )
2. 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一直线上,则三角板ABC旋转的度数是( ) A、60° B、90° C、120° D、150°3. 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα= ,则小车上升的高度是( )
A、60° B、90° C、120° D、150°3. 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα= ,则小车上升的高度是( )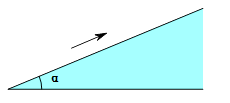 A、5米 B、6米 C、6.5米 D、12米4. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
A、5米 B、6米 C、6.5米 D、12米4. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )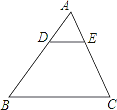 A、
A、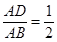 B、
B、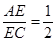 C、
C、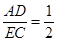 D、
D、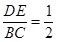 5. 已知,C是线段AB的黄金分割点,AC<BC,若AB=2,则BC=( )A、3﹣ B、 ( +1) C、 ﹣1 D、 ( ﹣1)6. 如图,正方形ABCD中,分别以B,D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
5. 已知,C是线段AB的黄金分割点,AC<BC,若AB=2,则BC=( )A、3﹣ B、 ( +1) C、 ﹣1 D、 ( ﹣1)6. 如图,正方形ABCD中,分别以B,D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )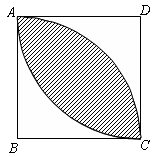 A、
A、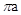 B、
B、 C、
C、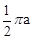 D、
D、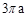 7. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( )
7. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC相似的是( ) A、
A、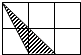 B、
B、 C、
C、 D、
D、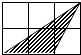 8. 二次函数y=(x﹣a)(x﹣b)﹣2,(a<b)的图象与x轴交点的横坐标为m,n,且m<n,则a,b,m,n的大小关系是( )A、a<m<n<b B、a<m<b<n C、m<a<b<n D、m<a<n<b9. 已知∠ADB,作图.
8. 二次函数y=(x﹣a)(x﹣b)﹣2,(a<b)的图象与x轴交点的横坐标为m,n,且m<n,则a,b,m,n的大小关系是( )A、a<m<n<b B、a<m<b<n C、m<a<b<n D、m<a<n<b9. 已知∠ADB,作图.步骤1:以点D为圆心,适当长为半径画弧,分别交DA、DB于点M、N;再分别以点M、N为圆心,大于 MN长为半径画弧交于点E,画射线DE.
步骤2:在DB上任取一点O,以点O为圆心,OD长为半径画半圆,分别交DA、DB、DE于点P、Q、C;
步骤3:连结PQ、OC.则下列判断:① ;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
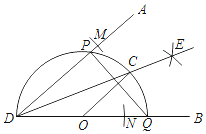 A、①③④ B、①②④ C、②③④ D、①②③④10. 已知函数y=mx2+nx﹣3,且2m﹣n=1,若不论m取何正数时,函数值y都随自变量x的增大而减小,则满足条件的x的取值范围是( )A、﹣4≤x≤﹣2 B、-2≤x≤- C、1<x≤3 D、3≤x≤5
A、①③④ B、①②④ C、②③④ D、①②③④10. 已知函数y=mx2+nx﹣3,且2m﹣n=1,若不论m取何正数时,函数值y都随自变量x的增大而减小,则满足条件的x的取值范围是( )A、﹣4≤x≤﹣2 B、-2≤x≤- C、1<x≤3 D、3≤x≤5二、填空题
-
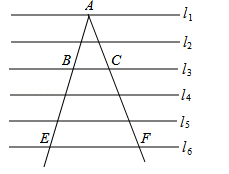
11. 若7x=3y,则 = .12. 如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是 .
 13. 如图,某小型水库栏水坝的横断面是四边形ABCD , DC∥AB , 测得迎水坡的坡角α=30°,已知背水坡的坡比为1.2:1,坝顶部DC宽为2m , 坝高为6m , 则坝底AB的长为m .
13. 如图,某小型水库栏水坝的横断面是四边形ABCD , DC∥AB , 测得迎水坡的坡角α=30°,已知背水坡的坡比为1.2:1,坝顶部DC宽为2m , 坝高为6m , 则坝底AB的长为m . 14. 已知函数y=x2+mx-2(m为常数),该函数的图象与x轴交点的个数是 .15. 如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O, =90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为cm2 .
14. 已知函数y=x2+mx-2(m为常数),该函数的图象与x轴交点的个数是 .15. 如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O, =90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为cm2 .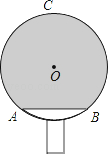 16. 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(如∠O)为60°,A,B,C,D都在格点上,且线段AB、CD相交于点P,则∠APC的正切值为 .
16. 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(如∠O)为60°,A,B,C,D都在格点上,且线段AB、CD相交于点P,则∠APC的正切值为 .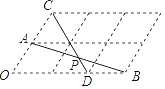
三、解答题
-
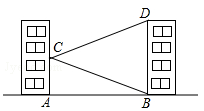
17. 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
 (1)、求∠BCD的度数.(2)、求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)18. 节能灯根据使用寿命分成优等品、正品和次品三个等级,其中使用寿命大于或等于8000小时的节能灯是优等品,使用寿命小于6000小时的节能灯是次品,其余的节能灯是正品.质检部门对某批次的一种节能灯(共200个)的使用寿命进行追踪调查,并将结果整理成此表.
(1)、求∠BCD的度数.(2)、求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)18. 节能灯根据使用寿命分成优等品、正品和次品三个等级,其中使用寿命大于或等于8000小时的节能灯是优等品,使用寿命小于6000小时的节能灯是次品,其余的节能灯是正品.质检部门对某批次的一种节能灯(共200个)的使用寿命进行追踪调查,并将结果整理成此表.寿命(小时)
频数
频率
4000≤t≤5000
10
0.05
5000≤t<6000
20
a
6000≤t<7000
80
0.40
7000≤t<8000
b
0.15
8000≤t<9000
60
c
合计
200
1
(1)、根据分布表中的数据,写出a,b,c的值;(2)、某人从这200个节能灯中随机购买1个,求这种节能灯恰好不是次品的概率.
19. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .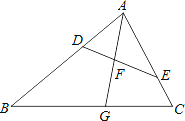 (1)、求证:△ADF∽△ACG;(2)、若 ,求 的值.20. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在 点上正方 的
(1)、求证:△ADF∽△ACG;(2)、若 ,求 的值.20. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在 点上正方 的 处发出一球,羽毛球飞行的高度 与水平距离 之间满足函数表达式 .已知点 与球网的水平距离为 ,球网的高度为 .
处发出一球,羽毛球飞行的高度 与水平距离 之间满足函数表达式 .已知点 与球网的水平距离为 ,球网的高度为 . 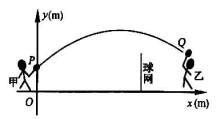 (1)、当 时,①求 的值.②通过计算判断此球能否过网.(2)、若甲发球过网后,羽毛球飞行到点 的水平距离为 ,离地面的高度为 的 处时,乙扣球成功,求 的值.21. 已知:如图,AB是⊙O的直径,点C、D为圆上两点,且CB=CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
(1)、当 时,①求 的值.②通过计算判断此球能否过网.(2)、若甲发球过网后,羽毛球飞行到点 的水平距离为 ,离地面的高度为 的 处时,乙扣球成功,求 的值.21. 已知:如图,AB是⊙O的直径,点C、D为圆上两点,且CB=CD,CF⊥AB于点F,CE⊥AD的延长线于点E.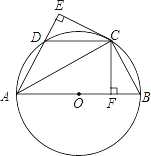 (1)、试说明:DE=BF;(2)、若∠DAB=60°,AB=6,求CF的长.22. 如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).
(1)、试说明:DE=BF;(2)、若∠DAB=60°,AB=6,求CF的长.22. 如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,设移动时间为t(s).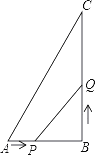 (1)、当t=4时,求△PBQ的面积;(2)、当t为多少时,四边形APQC的面积最小?最小面积是多少?(3)、当t为多少时,△PQB与△ABC相似.23. 二次函数y= 的图象与x轴交于点A和点B,以AB为边在x轴下方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)、当t=4时,求△PBQ的面积;(2)、当t为多少时,四边形APQC的面积最小?最小面积是多少?(3)、当t为多少时,△PQB与△ABC相似.23. 二次函数y= 的图象与x轴交于点A和点B,以AB为边在x轴下方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.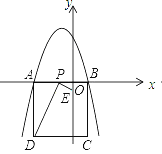 (1)、求出m的值并求出点A、点B的坐标.(2)、当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;(3)、是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
(1)、求出m的值并求出点A、点B的坐标.(2)、当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;(3)、是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.