云南省2019届数学中考模拟试卷(一)
试卷更新日期:2019-03-26 类型:中考模拟
一、单选题
-
1. 一个数用科学记数法表示为2.37×105 , 则这个数是( )A、237 B、2370 C、23700 D、2370002. 下列运算正确的是( )A、3a+2a=5a2 B、3﹣3=
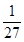 C、2a2•a2=2a6
D、60=0
3. 在正方形,矩形,菱形,平行四边形,正五边形五个图形中,中心对称图形的个数是( )A、2 B、3 C、4 D、54. 在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣4,﹣1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(﹣2,2),则点B′的坐标为( )A、(4,3) B、(3,4) C、(﹣1,﹣2) D、(﹣2,﹣1)5. 下面空心圆柱形物体的左视图是( )
C、2a2•a2=2a6
D、60=0
3. 在正方形,矩形,菱形,平行四边形,正五边形五个图形中,中心对称图形的个数是( )A、2 B、3 C、4 D、54. 在平面直角坐标系中,已知线段AB的两个端点分别是A(﹣4,﹣1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(﹣2,2),则点B′的坐标为( )A、(4,3) B、(3,4) C、(﹣1,﹣2) D、(﹣2,﹣1)5. 下面空心圆柱形物体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,下列哪个不等式组的解集在数轴上表示如图所示( )
6. 如图,下列哪个不等式组的解集在数轴上表示如图所示( )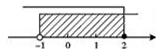 A、
A、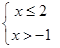 B、
B、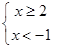 C、
C、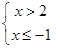 D、
D、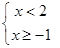 7. 某鞋店一天卖出运动鞋12双,其中各种尺码的鞋的销售量如下表:则这12双鞋的尺码组成的一组数据中,众数和中位数分别是( )
7. 某鞋店一天卖出运动鞋12双,其中各种尺码的鞋的销售量如下表:则这12双鞋的尺码组成的一组数据中,众数和中位数分别是( )码(cm)
23.5
24
24.5
25
25.5
销售量(双)
1
2
2
5
2
A、25,25 B、24.5,25 C、25,24.5 D、24.5,24.58. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )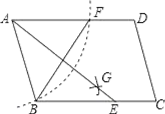 A、
A、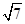 B、2
B、2 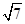 C、3
C、3 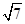 D、4
D、4 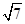
二、填空题
-
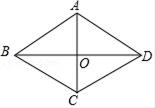
9. |﹣2|的相反数是 .10. 已知函数关系式:y= ,则自变量x的取值范围是 .11. 若x、y为实数,且|x+3|+ =0,则 的值为 .12. 如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是(只需添加一个即可)
 13. 已知A(0,3),B(2,3)是抛物线 上两点,该抛物线的顶点坐标是.14. 为了求1+3+32+33+…+3100的值,可令M=1+3+32+33+…+3100 , 则3M=3+32+33+34+…+3101 , 因此,3M﹣M=3101﹣1,所以M= ,即1+3+32+33+…+3100= ,仿照以上推理计算:1+5+52+53+…+52015的值是 .
13. 已知A(0,3),B(2,3)是抛物线 上两点,该抛物线的顶点坐标是.14. 为了求1+3+32+33+…+3100的值,可令M=1+3+32+33+…+3100 , 则3M=3+32+33+34+…+3101 , 因此,3M﹣M=3101﹣1,所以M= ,即1+3+32+33+…+3100= ,仿照以上推理计算:1+5+52+53+…+52015的值是 .三、解答题
-
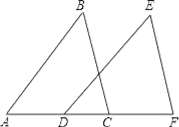
15. 先化简,再求值:(1+ )÷ ,其中x= ﹣1.16. 已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:AB=DE.
 17. 当前,“校园ipad现象已经受到社会的广泛关注,某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理:
17. 当前,“校园ipad现象已经受到社会的广泛关注,某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理:频数分布表
看法
频数
频率
赞成
5
无所谓
0.1
反对
40
0.8
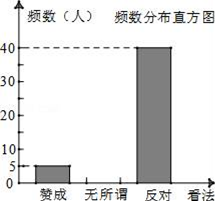 (1)、请求出共调查了多少人;并把小文整理的图表补充完整;(2)、小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?(3)、若该校有3000名学生,请您估计该校持“反对”态度的学生人数.18. 学校运动会上,九(1)班啦啦队买了两种矿泉水,其中甲种矿泉水共花费80元,乙种矿泉水共花费60元.甲种矿泉水比乙种矿泉水多买20瓶,且乙种矿泉水的价格是甲种矿泉水价格的1.5倍.求甲、乙两种矿泉水的价格.19. 有四张正面分别标有数字﹣1,0,1,2的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.(1)、随机抽取一张卡片,求抽到数字“﹣1”的概率;(2)、随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率.20. 某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y= 的一部分,请根据图中信息解答下列问题:
(1)、请求出共调查了多少人;并把小文整理的图表补充完整;(2)、小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?(3)、若该校有3000名学生,请您估计该校持“反对”态度的学生人数.18. 学校运动会上,九(1)班啦啦队买了两种矿泉水,其中甲种矿泉水共花费80元,乙种矿泉水共花费60元.甲种矿泉水比乙种矿泉水多买20瓶,且乙种矿泉水的价格是甲种矿泉水价格的1.5倍.求甲、乙两种矿泉水的价格.19. 有四张正面分别标有数字﹣1,0,1,2的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.(1)、随机抽取一张卡片,求抽到数字“﹣1”的概率;(2)、随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率.20. 某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y= 的一部分,请根据图中信息解答下列问题: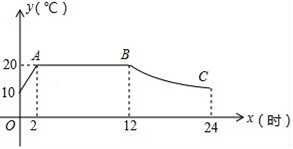 (1)、求0到2小时期间y随x的函数解析式;(2)、恒温系统在一天内保持大棚内温度不低于15℃的时间有多少小时?21. 如图,在▱ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
(1)、求0到2小时期间y随x的函数解析式;(2)、恒温系统在一天内保持大棚内温度不低于15℃的时间有多少小时?21. 如图,在▱ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.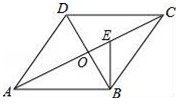 (1)、求证:AC⊥BD;(2)、若AB=14,cos∠CAB= ,求线段OE的长.22. 如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
(1)、求证:AC⊥BD;(2)、若AB=14,cos∠CAB= ,求线段OE的长.22. 如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.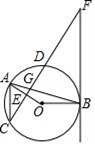 (1)、求证:FG=FB.(2)、若tan∠F= ,⊙O的半径为4,求CD的长.23. 如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
(1)、求证:FG=FB.(2)、若tan∠F= ,⊙O的半径为4,求CD的长.23. 如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a. (1)、求△ACD的面积(用含a的代数式表示);(2)、求点D到射线BN的距离(用含有a的代数式表示);(3)、是否存在点C,使△ACE是以AE为腰的等腰三角形?若存在,请求出此时a的值;若不存在,请说明理由.
(1)、求△ACD的面积(用含a的代数式表示);(2)、求点D到射线BN的距离(用含有a的代数式表示);(3)、是否存在点C,使△ACE是以AE为腰的等腰三角形?若存在,请求出此时a的值;若不存在,请说明理由.