辽宁省葫芦岛市龙港区2018年数学毕业升学考试模拟试卷
试卷更新日期:2019-03-26 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、﹣ C、﹣ D、
-
2. 在平面直角坐标系中,点(﹣1,﹣2)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
3. 如图,A,B,C是⊙O上的三点,∠BAC=30°,则∠BOC的大小是( )
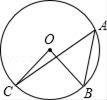 A、30° B、60° C、90° D、45°
A、30° B、60° C、90° D、45° -
4. 一元二次方程x2+2x+4=0的根的情况是( )A、有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根
-
5. 在Rt△ABC中,∠C=90°,a=1,c=4,则sinA的值是( )
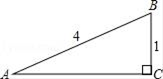 A、
A、 B、
C、
B、
C、 D、
D、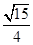
-
6. 如图,直线y=kx+b与x轴交于点(﹣4,0),则y>0时,x的取值范围是( )
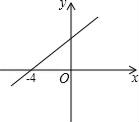 A、x>﹣4 B、x>0 C、x<﹣4 D、x<0
A、x>﹣4 B、x>0 C、x<﹣4 D、x<0 -
7. 将一圆形纸片对折后再对折,得到下图,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( )
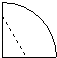 A、
A、 B、
B、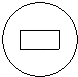 C、
C、 D、
D、
二、填空题
-
8. 早春二月的某一天,大连市南部地区的平均气温为﹣3℃,北部地区的平均气温为﹣6℃,则当天南部地区比北部地区的平均气温高℃.
-
9. 在函数y= 中,自变量x的取值范围是 .
-
10. 关于x的一元二次方程x2+bx+c=0的两根为x1=1,x2=2,则x2+bx+c分解因式的结果为 .
-
11. 如图,⊙O的半径为5cm,圆心O到AB的距离为3cm,则弦AB长为 cm.

-
12. 大连市内与庄河两地之间的距离是160千米,若汽车以平均每小时80千米的速度从大连市内开往庄河,则汽车距庄河的路程y(千米)与行驶的时间x(小时)之间的函数关系式为 .
-
13. 边长为6的正六边形外接圆半径是 .
-
14. 将一个底面半径为2,高为4的圆柱形纸筒沿一条母线剪开,所得到的侧面展开图形面积为 .
三、解答题
-
15. 反比例函数 的图象经过点A (2,-3) .
(1)、求这个函数的解析式;(2)、请判断点B(1,6)是否在这个反比例函数的图象上,并说明理由. -
16. 如图,某校自行车棚的人字架棚顶为等腰三角形,D是AB的中点,中柱CD=1米,∠A=27°,求跨度AB的长(精确到0.01米).
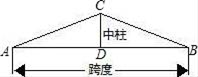
-
17. 解方程组 .
-
18. 某工程队承担了修建长30米地下通道的任务,由于工作需要,实际施工时每周比原计划多修1米,结果比原计划提前1周完成.求该工程队原计划每周修建多少米?
-
19. 如图,AB、CD是⊙O的直径,DF、BE是弦,且DF=BE,求证:∠D=∠B.
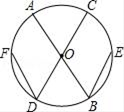
-
20. 未成年人思想道德建设越来越受到社会的关注,辽阳青少年研究所随机调查了本市一中学100名学生寒假中花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成了频率分布表和频率分布直方图(如图).
分组
频数
频率
0.5~50.5
0.1
50.5~
20
0.2
100.5~150.5
200.5
30
0.3
200.5~250.5
10
0.1
 (1)、补全频率分布表;(2)、在频率分布直方图中,长方形ABCD的面积是;这次调查的样本容量是;(3)、研究所认为,应对消费150元以上的学生提出勤俭节约的建议.试估计应对该校1000名学生中约多少名学生提出这项建议.
(1)、补全频率分布表;(2)、在频率分布直方图中,长方形ABCD的面积是;这次调查的样本容量是;(3)、研究所认为,应对消费150元以上的学生提出勤俭节约的建议.试估计应对该校1000名学生中约多少名学生提出这项建议. -
21. 如图,抛物线y=﹣x2+5x+n经过点A(1,0),与y轴交于点B.
 (1)、求抛物线的解析式;(2)、P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
(1)、求抛物线的解析式;(2)、P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标. -
22. 如图1,图2…、图m是边长均大于2的三角形、四边形、…、凸n边形.分别以它们的各顶点为圆心,以1为半径画弧与两邻边相交,得到3条弧、4条弧…、n条弧.
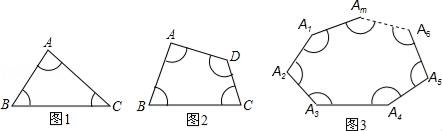 (1)、图1中3条弧的弧长的和为 , 图2中4条弧的弧长的和为;(2)、求图m中n条弧的弧长的和(用n表示).
(1)、图1中3条弧的弧长的和为 , 图2中4条弧的弧长的和为;(2)、求图m中n条弧的弧长的和(用n表示). -
23. 4×100米拉力赛是学校运动会最精彩的项目之一.图中的实线和虚线分别是初三•一班和初三•二班代表队在比赛时运动员所跑的路程y(米)与所用时间x(秒)的函数图象(假设每名运动员跑步速度不变,交接棒时间忽略不计).问题:
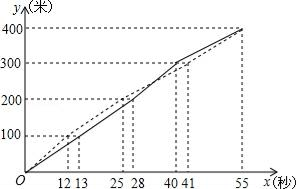 (1)、初三•二班跑得最快的是第接力棒的运动员;(2)、发令后经过多长时间两班运动员第一次并列?
(1)、初三•二班跑得最快的是第接力棒的运动员;(2)、发令后经过多长时间两班运动员第一次并列? -
24. 如图,⊙O的直径DF与弦AB交于点E,C为⊙O外一点,CB⊥AB,G是直线CD上一点,∠ADG=∠ABD.
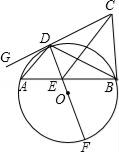
求证:AD•CE=DE•DF;
说明:
(1)、如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路过程写出来(要求至少写3步);(2)、在你经历说明(1)的过程之后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.①∠CDB=∠CEB;
②AD∥EC;
③∠DEC=∠ADF,且∠CDE=90°.
-
25. 阅读材料,解答问题.
材料:“小聪设计的一个电子游戏是:一电子跳蚤从这P1(﹣3,9)开始,按点的横坐标依次增加1的规律,在抛物线y=x2上向右跳动,得到点P2、P3、P4、P5…(如图1所示).过P1、P2、P3分别作P1H1、P2H2、P3H3垂直于x轴,垂足为H1、H2、H3 , 则S△P1P2P3=S梯形P1H1H3P3﹣S梯形P1H1H2P2﹣S梯形P2H2H3P3= (9+1)×2﹣ (9+4)×1﹣ (4+1)×1,即△P1P2P3的面积为1.”

问题:
(1)、求四边形P1P2P3P4和P2P3P4P5的面积(要求:写出其中一个四边形面积的求解过程,另一个直接写出答案);(2)、猜想四边形Pn﹣1PnPn+1Pn+2的面积,并说明理由(利用图2);(3)、若将抛物线y=x2改为抛物线y=x2+bx+c,其它条件不变,猜想四边形Pn﹣1PnPn+1Pn+2的面积(直接写出答案). -
26. 初三(5)班综合实践小组去湖滨花园测量人工湖的长,如图A、D是人工湖边的两座雕塑,AB、BC是湖滨花园的小路,小东同学进行如下测量,B点在A点北偏东60°方向,C点在B点北偏东45°方向,C点在D点正东方向,且测得AB=20米,BC=40米,求AD的长.( ≈1.732, ≈1.414,结果精确到0.01米)

