湖北省荆门市2019届九年级中考数学二模试题
试卷更新日期:2019-03-26 类型:中考模拟
一、单选题
-
1. 下列各数中,没有平方根的是( )A、
 B、
B、 C、
C、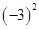 D、
D、 2. 下列运算正确的是( )A、
2. 下列运算正确的是( )A、 =﹣3
B、a2•a4=a6
C、(2a2)3=2a6
D、(a+2)2=a2+4
3. 某种计算机完成一次基本运算的时间约为0.000 000 001 s,把0.000 000 001 s用科学记数法可表示为( )A、0.1×10-8 s B、0.1×10-9 s C、1×10-8 s D、1×10-9 s4. 由6个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是( )
=﹣3
B、a2•a4=a6
C、(2a2)3=2a6
D、(a+2)2=a2+4
3. 某种计算机完成一次基本运算的时间约为0.000 000 001 s,把0.000 000 001 s用科学记数法可表示为( )A、0.1×10-8 s B、0.1×10-9 s C、1×10-8 s D、1×10-9 s4. 由6个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是( ) A、正视图的面积最大 B、左视图的面积最大 C、俯视图的面积最大 D、三个视图的面积一样大5. 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( )
A、正视图的面积最大 B、左视图的面积最大 C、俯视图的面积最大 D、三个视图的面积一样大5. 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.如果∠2=60°,那么∠1的度数为( ) A、60° B、50° C、40° D、30°6. 若整数k满足k< <k+1,则k的值是( )A、6 B、7 C、8 D、97. 已知关于x的方程x2﹣2x+3k=0有两个不相等的实数根,则k的取值范围是( )A、k<
A、60° B、50° C、40° D、30°6. 若整数k满足k< <k+1,则k的值是( )A、6 B、7 C、8 D、97. 已知关于x的方程x2﹣2x+3k=0有两个不相等的实数根,则k的取值范围是( )A、k< B、k>-
B、k>-  C、k<
C、k<  且k≠0
D、k>-
且k≠0
D、k>-  且k≠0
8. 如果关于x的不等式组 的解集为x<7,则m的取值范围为( )A、m=7 B、m>7 C、m<7 D、m≥79. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )
且k≠0
8. 如果关于x的不等式组 的解集为x<7,则m的取值范围为( )A、m=7 B、m>7 C、m<7 D、m≥79. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( ) A、小明中途休息用了20分钟 B、小明休息前爬山的平均速度为每分钟70米 C、小明在上述过程中所走的路程为6600米 D、小明休息前爬山的平均速度大于休息后爬山的平均速度10. 已知2是关于x的方程x2﹣(5+m)x+5m=0的一个根,并且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )A、9 B、12 C、9或12 D、6或12或1511. 如图,四边形ABCD是平行四边形,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则∠AEB的正切值为( )
A、小明中途休息用了20分钟 B、小明休息前爬山的平均速度为每分钟70米 C、小明在上述过程中所走的路程为6600米 D、小明休息前爬山的平均速度大于休息后爬山的平均速度10. 已知2是关于x的方程x2﹣(5+m)x+5m=0的一个根,并且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )A、9 B、12 C、9或12 D、6或12或1511. 如图,四边形ABCD是平行四边形,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则∠AEB的正切值为( ) A、 B、 C、
A、 B、 C、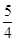 D、
D、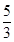 12. 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点,过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P从点A运动到点D时,点Q所经过的路径长为( )
12. 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点,过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P从点A运动到点D时,点Q所经过的路径长为( ) A、
A、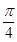 B、
B、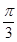 C、
C、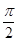 D、π
D、π
二、填空题
-
13. 分解因式 的结果是 .
14. 美术馆举办的一次画展中,展出的油画作品和国画作品共有100幅,其中油画作品数量是国画作品数量的2倍多7幅,则展出的油画作品有幅.15. 如图,双曲线y= 于直线y=﹣ x交于A、B两点,且A(﹣2,m),则点B的坐标是 . 16. 当x=m或x=n(m≠n)时,代数式x2﹣2x+4的值相等,则当x=m+n时,代数式x2﹣2x+4的值为 .17. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .
16. 当x=m或x=n(m≠n)时,代数式x2﹣2x+4的值相等,则当x=m+n时,代数式x2﹣2x+4的值为 .17. 如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .
三、解答题
-
18.(1)、计算:|2﹣ |+2sin60°+( )﹣1﹣( )0;(2)、解二元一次方程组 .19. 某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类记为A;音乐类记为B;球类记为C;其他类记为D.根据调查结果发现该班每个学生都进行了等级且只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生都进行了归类,并制作了如下两幅统计图,请你结合图中所给信息解答下列问题:
 (1)、七年级(1)班学生总人数为人,扇形统计图中D类所对应扇形的圆心角为度,请补全条形统计图;(2)、学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.20. 在△ABC中,∠B=90°,AB=BC,点D是BC边上的一点,连接AD,将AD绕点D顺时针旋转90°得到DE,作EF⊥BC交BC的延长线于点F.
(1)、七年级(1)班学生总人数为人,扇形统计图中D类所对应扇形的圆心角为度,请补全条形统计图;(2)、学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.20. 在△ABC中,∠B=90°,AB=BC,点D是BC边上的一点,连接AD,将AD绕点D顺时针旋转90°得到DE,作EF⊥BC交BC的延长线于点F. (1)、依题意补全图形;(2)、求证:EF=CF.21. 某市一种出租车起步价是5元(路程在3km以内均付5元),达到或超过3km,每增加0.5km加价0.7元(不足0.5km按0.5km计).某乘客坐这种出租车从甲地到乙地,下车时付车费14.8元,那么甲地到乙地的路程是多少?22. 如图,在某海上观测点B处观测到位于北偏东30°方向有一艘救船A,搜救船A最大航速50海里/时,AB=52 海里,在位于观测点B的正东方向,搜救船A的东南方向有一失事渔船C,由于当天正值东南风,失事渔船C以2海里/时的速度向西北方向漂移,若不考虑大风对搜救船A的航线和航速的影响,求失事渔船获救的最快时间.
(1)、依题意补全图形;(2)、求证:EF=CF.21. 某市一种出租车起步价是5元(路程在3km以内均付5元),达到或超过3km,每增加0.5km加价0.7元(不足0.5km按0.5km计).某乘客坐这种出租车从甲地到乙地,下车时付车费14.8元,那么甲地到乙地的路程是多少?22. 如图,在某海上观测点B处观测到位于北偏东30°方向有一艘救船A,搜救船A最大航速50海里/时,AB=52 海里,在位于观测点B的正东方向,搜救船A的东南方向有一失事渔船C,由于当天正值东南风,失事渔船C以2海里/时的速度向西北方向漂移,若不考虑大风对搜救船A的航线和航速的影响,求失事渔船获救的最快时间. 23. 如图,半圆O的直径AB=20,弦CD∥AB,动点M在半径OD上,射线BM与弦CD相交于点E(点E与点C、D不重合),设OM=m.
23. 如图,半圆O的直径AB=20,弦CD∥AB,动点M在半径OD上,射线BM与弦CD相交于点E(点E与点C、D不重合),设OM=m. (1)、求DE的长(用含m的代数式表示);(2)、令弦CD所对的圆心角为α,且sin .
(1)、求DE的长(用含m的代数式表示);(2)、令弦CD所对的圆心角为α,且sin .①若△DEM的面积为S,求S关于m的函数关系式,并求出m的取值范围;
②若动点N在CD上,且CN=OM,射线BM与射线ON相交于点F,当∠OMF=90° 时,求DE的长.
24. 如图,抛物线y=x2﹣mx﹣(m+1)与x轴负半轴交于点A(x1 , 0),与x轴正半轴交于点B(x2 , 0)(OA<OB),与y轴交于点C,且满足x12+x22﹣x1x2=13. (1)、求抛物线的解析式;(2)、以点B为直角顶点,BC为直角边作Rt△BCD,CD交抛物线于第四象限的点E,若EC=ED,求点E的坐标;(3)、在抛物线上是否存在点Q,使得S△ACQ=2S△AOC?若存在,求出点Q的坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、以点B为直角顶点,BC为直角边作Rt△BCD,CD交抛物线于第四象限的点E,若EC=ED,求点E的坐标;(3)、在抛物线上是否存在点Q,使得S△ACQ=2S△AOC?若存在,求出点Q的坐标;若不存在,说明理由.