浙江省绍兴市越城区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期：2019-03-26 类型：期末考试
一、选择题
-
1. ﹣2019的相反数是（ ）A、﹣2019 B、﹣
C、2019
D、
2. 在下列五个数中① ，② ，③ ，④0.777…，⑤2π，是无理数的是（ ）A、①③⑤ B、①②⑤ C、①④ D、①⑤3. 据科学家估计，地球的年龄大约是4600000000年，将4600000000用科学记数法表示为（ ）A、4.6×108 B、46×108 C、4.69 D、4.6×1094. 将5041精确到百位的结果是（ ）A、5000 B、5.0×103 C、50 D、5.04×1035. 下列说法正确的是（ ）A、立方根是它本身的数只能是0和1 B、如果一个数有立方根，那么这个数也一定有平方根 C、16的平方根是4 D、﹣2是4的一个平方根6. 下列代数式 ，x2+x﹣ ， ， ，其中整式有（ ）A、1个 B、2个 C、3个 D、4个7. 设a是最小的自然数，b是最小的正整数，c是最大的负整数，则a、b、c三数之和为（ ）A、﹣1 B、0 C、1 D、28. 如图，若A是实数a在数轴上对应的点，则关于a，﹣a，1的大小关系表示正确的是（ ）
A、a＜1＜﹣a B、a＜﹣a＜1 C、1＜﹣a＜a D、﹣a＜a＜19. 若 与 互为相反数，则m的值为（ ）A、
B、
C、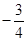
D、
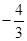10.填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（ ）
A、38 B、52 C、66 D、74二、填空题
-
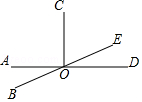
11. 的系数是 ．12. 把53°24′用度表示为 ．13. 若﹣7xay3与x2ya+b是同类项，则b＝ ．14. 如图，直线AD与BE相交于点O，∠COD＝90°，∠COE＝70°，则∠AOB＝ ．
15. 关于x的方程2x+5a＝3的解与方程2x+2＝0的解相同，则a的值是 ．16. 如图，点C在线段AB的延长线上，BC＝2AB，点D是线段AC的中点，AB＝2cm，则BD的长度是 ．
17. 当x＝2时，代数式ax3+bx﹣3的值为9，那么，当x＝﹣2时代数式ax3+bx+5的值为 ．18. 小明在数轴上先作边长为1的正方形，再用圆规画出了点A（如图所示），则点A所表示的数为 ．
三、简答题
-
19. 计算(1)、(2)、（﹣30）×（ ﹣ + ）(3)、(4)、﹣22+（﹣2）2+ +（﹣1）201720. 化简并求值：2（a2﹣ab）﹣3（b2﹣ ab），其中a＝﹣3，b＝3．21. 解方程(1)、3（x﹣1）+6＝2（x+3）+7(2)、1+ ＝ ．22. A、B两地相距450千米，甲，乙两车分别从A、B两地同时出发，相向而行．已知甲车速度为120千米/时，乙车速度为80千米/时，经过多少小时两车相距50千米？23. 聪聪是一位非常喜欢动脑筋的初一学生，特别是学了几何后，更觉得数学奇妙，当聪聪学完《图形的初步知识》后对角平分线兴趣更浓厚，下面请你和聪聪同学一起来探究奇妙的角平分线吧．已知∠AOB＝100°，射线OE，OF分别是∠AOC和∠COB的角平分线．
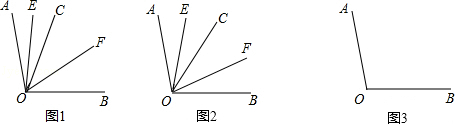(1)、如图1，若射线OC在∠AOB的内部，且∠AOC＝30°，求∠EOF的度数；(2)、如图2，若射线OC在∠AOB的内部绕点O旋转，且∠AOC＝40°，求∠EOF的度数；(3)、若射线OC在∠AOB的外部绕点O旋转（旋转中∠AOC，∠BOC均指小于180°的角），其余条件不变，请借助图3探究∠BOF的大小，请直接写出∠EOF的度数（不写探究过程）24. 已知数轴上有两点A、B，点A对应的数是40，点B对应的数是﹣80．(1)、求线段AB的长．(2)、如图，O表示原点，动点P、T分别从B、O两点同时出发向左运动，同时动点Q从点A出发向右运动，点P、T、Q的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒，设运动时间为t．
①求点P、T、Q表示的数（用含有t的代数式表示）；
②在运动过程中，如果点M为线段PT的中点，点N为线段OQ的中点，试说明在运动过程中等量关系PQ+OT＝2MN始终成立．