陕西省2019届九年级初中毕业学业考试模拟考试数学卷(二)
试卷更新日期:2019-03-26 类型:中考模拟
一、单选题
-
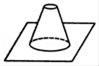
1. 在﹣3,0,4, 这四个数中,最大的数是A、﹣3 B、0 C、4 D、2. 如图是一个放置在水平桌面的锥形瓶,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、﹣3a+a=﹣4a B、3x2•2x=6x2 C、4a2﹣5a2=a2 D、(2x3)2÷2x2=2x44. 如图,AB∥CD,AD与BC相交于点O,若∠A=50°10′,∠COD=100°,则∠C等于( )
3. 下列运算正确的是( )A、﹣3a+a=﹣4a B、3x2•2x=6x2 C、4a2﹣5a2=a2 D、(2x3)2÷2x2=2x44. 如图,AB∥CD,AD与BC相交于点O,若∠A=50°10′,∠COD=100°,则∠C等于( ) A、30°10′ B、29°10′ C、29°50′ D、50°10′5. 若点M(﹣3,y1),N(﹣4,y2)都在正比例函数y=﹣k2x(k≠0)的图象上,则y1与y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定6. 如图,在△ABC中,AB=AC=3,BC=4,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是( )
A、30°10′ B、29°10′ C、29°50′ D、50°10′5. 若点M(﹣3,y1),N(﹣4,y2)都在正比例函数y=﹣k2x(k≠0)的图象上,则y1与y2的大小关系是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定6. 如图,在△ABC中,AB=AC=3,BC=4,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是( ) A、3 B、4 C、5 D、67. 将直线y=﹣x+a的图象向右平移2个单位后经过点A(3,3),则a的值为( )A、4 B、﹣4 C、2 D、﹣28. 如图,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,分别以AB,BC,DC为边向外作正方形,它们的面积分别为S1、S2、S3 . 若S2=48,S3=9,则S1的值为( )
A、3 B、4 C、5 D、67. 将直线y=﹣x+a的图象向右平移2个单位后经过点A(3,3),则a的值为( )A、4 B、﹣4 C、2 D、﹣28. 如图,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,分别以AB,BC,DC为边向外作正方形,它们的面积分别为S1、S2、S3 . 若S2=48,S3=9,则S1的值为( )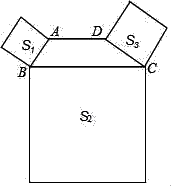 A、18 B、12 C、9 D、39. 如图,AB是 的直径,点C,D在 上,若 ,则 的度数为
A、18 B、12 C、9 D、39. 如图,AB是 的直径,点C,D在 上,若 ,则 的度数为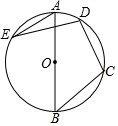 A、
A、 B、
B、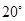 C、
C、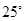 D、
D、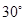 10. 若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数 ( )A、有最大值
10. 若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数 ( )A、有最大值 B、有最大值﹣
B、有最大值﹣  C、有最小值
C、有最小值  D、有最小值﹣
D、有最小值﹣ 
二、填空题
-
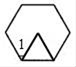
11. 比较大小: .(填“<“,“=“,“>“)12. 如图,在同一平面内,将边长相等的正三角形和正六边形的一条边重合并叠在一起,则∠1的度数为 .
 13. 如图,已知反比例函数y= (x>0)的图象经过Rt△OAB斜边OB的中点C,且与直角边AB交于点D,连接OD,若点B的坐标为(2,3),则△OAD的面积为 .
13. 如图,已知反比例函数y= (x>0)的图象经过Rt△OAB斜边OB的中点C,且与直角边AB交于点D,连接OD,若点B的坐标为(2,3),则△OAD的面积为 . 14. 如图,在⊙O中,点B为半径OA上一点,且OA=13,AB=1,若CD是一条过点B的动弦,则弦CD的最小值为 .
14. 如图,在⊙O中,点B为半径OA上一点,且OA=13,AB=1,若CD是一条过点B的动弦,则弦CD的最小值为 .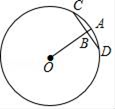
三、解答题
-
15. 计算:(π﹣2)0+|﹣1|﹣ ÷ +(﹣1)﹣2 .16. 解不等式组 ,并将它的解集在数轴上表示出来.17. 如图,已知∠AOB与点M、N求作一点P,使点P到边OA、OB的距离相等,且PM=PN(保留作图痕迹,不写作法)
 18. 某市为了解本地七年级学生寒假期间参加社会实践活动情况,随机抽查了部分七年级学生寒假参加社会实践活动的天数(“A﹣﹣﹣不超过5天”、“B﹣﹣﹣6天”、“C﹣﹣﹣7天”、“D﹣﹣﹣8天”、“E﹣﹣﹣9天及以上”),并将得到的数据绘制成如下两幅不完整的统计图.
18. 某市为了解本地七年级学生寒假期间参加社会实践活动情况,随机抽查了部分七年级学生寒假参加社会实践活动的天数(“A﹣﹣﹣不超过5天”、“B﹣﹣﹣6天”、“C﹣﹣﹣7天”、“D﹣﹣﹣8天”、“E﹣﹣﹣9天及以上”),并将得到的数据绘制成如下两幅不完整的统计图.
请根据以上的信息,回答下列问题:
(1)、补全扇形统计图和条形统计图;(2)、所抽查学生参加社会实践活动天数的众数是(选填:A,B,C,D,E);(3)、若该市七年级约有2000名学生,请你估计参加社会实践“活动天数不少于7天”的学生大约有多少人?19. 如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE与BD相交于点O.求证:EC=ED.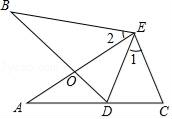 20. 小雁塔位于唐长安城安仁坊(今陕西省西安市南郊)荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.小明在学习了锐角三角函数后,想利用所学知识测量“小雁塔”的高度,小明在一栋高9.982米的建筑物底部D处测得塔顶端A的仰角为45°,接着在建筑物顶端C处测得塔顶端A的仰角为37.5°.已知AB⊥BD,CD⊥BD,请你根据题中提供的相关信息,求出“小雁塔”的高AB的长度(结果精确到1米)(参考数据:sin37.5°≈0.61,cos37.5°≈0.79,tan37.5°≈0.77)
20. 小雁塔位于唐长安城安仁坊(今陕西省西安市南郊)荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.小明在学习了锐角三角函数后,想利用所学知识测量“小雁塔”的高度,小明在一栋高9.982米的建筑物底部D处测得塔顶端A的仰角为45°,接着在建筑物顶端C处测得塔顶端A的仰角为37.5°.已知AB⊥BD,CD⊥BD,请你根据题中提供的相关信息,求出“小雁塔”的高AB的长度(结果精确到1米)(参考数据:sin37.5°≈0.61,cos37.5°≈0.79,tan37.5°≈0.77) 21. 春节期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
21. 春节期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.租车公司:按日收取固定租金80元,另外再按租车时间计费.
共享汽车:无固定租金,直接以租车时间(时)计费.
如图是两种租车方式所需费用y1(元)、y2(元)与租车时间x(时)之间的函数图象,

根据以上信息,回答下列问题:
(1)、分别求出y1、y2与x的函数表达式;(2)、请你帮助小丽一家选择合算的租车方案.22. 西安汇聚了很多人们耳熟能详的陕西美食.李华和王涛同时去选美食,李华准备在“肉夹馍(A)、羊肉泡馍(B)、麻酱凉皮(C)、(biang)面(D)”这四种美食中选择一种,王涛准备在“秘制凉皮(E)、肉丸胡辣汤(F)、葫芦鸡(G)、水晶凉皮(H)”这四种美食中选择一种.(1)、求李华选择的美食是羊肉泡馍的概率;(2)、请用画树状图或列表的方法,求李华和王涛选择的美食都是凉皮的概率.23. 如图,在△ABC中,以AB为直径的⊙O交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,且DH是⊙O的切线,连接DE交AB于点F. (1)、求证:DC=DE;(2)、若AE=1, ,求⊙O的半径.24. 如图,抛物线y=ax2+2x+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3).
(1)、求证:DC=DE;(2)、若AE=1, ,求⊙O的半径.24. 如图,抛物线y=ax2+2x+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,3). (1)、求该抛物线的解析式;(2)、在抛物线的对称轴上是否存在一点Q,使得以A、C、Q为顶点的三角形为直角三角形?若存在,试求出点Q的坐标;若不存在,请说明理由.25. 问题提出
(1)、求该抛物线的解析式;(2)、在抛物线的对称轴上是否存在一点Q,使得以A、C、Q为顶点的三角形为直角三角形?若存在,试求出点Q的坐标;若不存在,请说明理由.25. 问题提出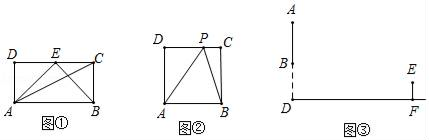 (1)、如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB∠ACB(填“>”“<”“=”);(2)、如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;
(1)、如图①,在矩形ABCD中,AB=2AD,E为CD的中点,则∠AEB∠ACB(填“>”“<”“=”);(2)、如图②,在正方形ABCD中,P为CD边上的一个动点,当点P位于何处时,∠APB最大?并说明理由;问题解决
(3)、如图③,在一幢大楼AD上装有一块矩形广告牌,其侧面上、下边沿相距6米(即AB=6米),下边沿到地面的距离BD=11.6米.如果小刚的睛睛距离地面的高度EF为1.6米,他从远处正对广告牌走近时,在P处看广告效果最好(视角最大),请你在图③中找到点P的位置,并计算此时小刚与大楼AD之间的距离.