江苏省南通市通州区2019届九年级数学中考二模试卷
试卷更新日期:2019-03-26 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、﹣2 B、 C、±2 D、22. 预计2019年建成通车的沪通长江大桥全长约11100米,将11100用科学记数法表示为( )A、1.11×105 B、1.11×104 C、0.111×106 D、11.1×1033. 下列图形中,是轴对称图形的是( )
A、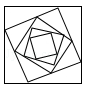 B、
B、 C、
C、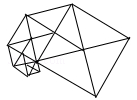 D、
D、 4. 下列计算正确的是( )A、a2+a2=a4 B、a5÷a2=a3 C、a3•a2=a6 D、(﹣a3)2=﹣a65. 若一个三角形的两边长分别为4和6,则第三边长可能是( )A、12 B、10 C、8 D、26. 一组数据2,4,x,6,8的众数为8,则这组数据的中位数为( )A、2 B、4 C、6 D、87. 若将半径为10cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( )A、5cm B、4cm C、3cm D、2cm8. 在平面直角坐标系中,已知点M(2,3),N(﹣1,﹣3),P(1,2),Q(﹣2,3),其中不可能与点A(2,﹣3)在同一函数图象上的一个点是( )A、点M B、点N C、点P D、点Q9. 如图,将矩形ABCD沿对角线AC折叠,使点B翻折到点E处,若 ,则 的值为( )
4. 下列计算正确的是( )A、a2+a2=a4 B、a5÷a2=a3 C、a3•a2=a6 D、(﹣a3)2=﹣a65. 若一个三角形的两边长分别为4和6,则第三边长可能是( )A、12 B、10 C、8 D、26. 一组数据2,4,x,6,8的众数为8,则这组数据的中位数为( )A、2 B、4 C、6 D、87. 若将半径为10cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( )A、5cm B、4cm C、3cm D、2cm8. 在平面直角坐标系中,已知点M(2,3),N(﹣1,﹣3),P(1,2),Q(﹣2,3),其中不可能与点A(2,﹣3)在同一函数图象上的一个点是( )A、点M B、点N C、点P D、点Q9. 如图,将矩形ABCD沿对角线AC折叠,使点B翻折到点E处,若 ,则 的值为( ) A、 B、
A、 B、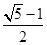 C、
C、 D、
D、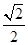 10. 已知直线y=﹣x+2与直线y=2x+6相交于点A,与x轴分别交于B,C两点,若点D(a, a+1)落在△ABC内部(不含边界),则a的取值范围是( )A、﹣3<a<2 B、
10. 已知直线y=﹣x+2与直线y=2x+6相交于点A,与x轴分别交于B,C两点,若点D(a, a+1)落在△ABC内部(不含边界),则a的取值范围是( )A、﹣3<a<2 B、 C、
C、 D、﹣2<a<2
D、﹣2<a<2
二、填空题
-
11. 不等式x﹣1≥2的解集是 .12. 若关于x的方程x2﹣8x+m=0有两个相等的实数根,则m= .13. 如图,直线a∥b,直线l与a,b分别交于A,B两点,过点B作BC⊥AB交直线a于点C,若∠1=35°,则∠2=度.
 14. 计算:40352﹣4×2017×2018= .15. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为尺.
14. 计算:40352﹣4×2017×2018= .15. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为尺.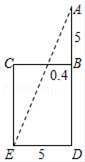 16. 如图,点A在反比例函数y= (x>0)的图象上,点B在反比例函数y= (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为 .
16. 如图,点A在反比例函数y= (x>0)的图象上,点B在反比例函数y= (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积为2,则k的值为 . 17. 如图,正方形ABCD的边长为6,E,F是对角线BD上的两个动点,且EF= ,
17. 如图,正方形ABCD的边长为6,E,F是对角线BD上的两个动点,且EF= ,连接CE,CF,则△CEF周长的最小值为 .

三、解答题
-
18.(1)、计算 ×cos45°﹣( )﹣1+20180;(2)、解方程组19. 已知代数式 .(1)、化简这个代数式;(2)、“当x=0时,该代数式的值为 ”,这个说法正确吗?请说明理由.20. 某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果为“A非常了解”、“B了解”、“C基本了解”三个等级,并根据调查结果制作了如下两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
 (1)、本次调查的人数为;(2)、补全条形统计图;(3)、若该市约有市民100万人,请你根据抽样调查的结果,估计该市大约有多少人对“社
(1)、本次调查的人数为;(2)、补全条形统计图;(3)、若该市约有市民100万人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A非常了解”的程度.
21. 在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个,黑球2个.(1)、若先从袋中取出x(x>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,若A为必然事件,则x的值为;(2)、若从袋中随机摸出2个球,正好红球、黑球各1个,用画树状图或列表法求这个事件的概率.22. 如图,菱形ABCD中,点E是边AD上一点,延长AB至点F,使BF=AE,连结BE,CF.求证:BE=CF. 23. 如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数, ≈1.72).
23. 如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数, ≈1.72).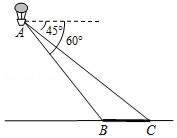 24. 如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
24. 如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D. (1)、求证:∠BAD+∠C=90°;(2)、求线段AD的长.25. A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).(1)、分别写出yA、yB与x的函数表达式;(2)、当yA=yB时,求x的值;(3)、当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元?26. 已知抛物线y=﹣x2+2kx﹣k2+k+3(k为常数)的顶点纵坐标为4.(1)、求k的值;(2)、设抛物线与直线y=﹣ (x﹣3)(m≠0)两交点的横坐标为x1 , x2 , n=x1+x2﹣2,若A(1,a),B(b, )两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;(3)、将(2)中的直线AB绕点(3,0)顺时针旋转45°,与抛物线x轴上方的部分相交于点C,请直接写出点C的坐标.27. 如图①,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点.
(1)、求证:∠BAD+∠C=90°;(2)、求线段AD的长.25. A厂一月份产值为16万元,因管理不善,二、三月份产值的月平均下降率为x(0<x<1).B厂一月份产值为12万元,二月份产值下降率为x,经过技术革新,三月份产值增长,增长率为2x.三月份A、B两厂产值分别为yA、yB(单位:万元).(1)、分别写出yA、yB与x的函数表达式;(2)、当yA=yB时,求x的值;(3)、当x为何值时,三月份A、B两厂产值的差距最大?最大值是多少万元?26. 已知抛物线y=﹣x2+2kx﹣k2+k+3(k为常数)的顶点纵坐标为4.(1)、求k的值;(2)、设抛物线与直线y=﹣ (x﹣3)(m≠0)两交点的横坐标为x1 , x2 , n=x1+x2﹣2,若A(1,a),B(b, )两点在动点M(m,n)所形成的曲线上,求直线AB的解析式;(3)、将(2)中的直线AB绕点(3,0)顺时针旋转45°,与抛物线x轴上方的部分相交于点C,请直接写出点C的坐标.27. 如图①,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点. (1)、如图②,在Rt△ABC中,∠B=60°,D为斜边AB的中点,E为AC的中点.求证:点D为C,E在直线AB上的投射点;(2)、如图③,在正方形网格中,已知点A,B,C三点均在格点上,请仅用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ;(3)、如图④,在Rt△ABC中,∠C=90°,AC=BC,在AB,BC边上是否分别存在点D,E,使点D为E,C在AB上的投射点,点E为A,D在BC上的投射点?若存在,求出 的值;若不存在,请说明理由.
(1)、如图②,在Rt△ABC中,∠B=60°,D为斜边AB的中点,E为AC的中点.求证:点D为C,E在直线AB上的投射点;(2)、如图③,在正方形网格中,已知点A,B,C三点均在格点上,请仅用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ;(3)、如图④,在Rt△ABC中,∠C=90°,AC=BC,在AB,BC边上是否分别存在点D,E,使点D为E,C在AB上的投射点,点E为A,D在BC上的投射点?若存在,求出 的值;若不存在,请说明理由.