河南省2019届数学中考模试试卷(一)
试卷更新日期:2019-03-26 类型:中考模拟
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、-
 D、
D、 2. 中国的陆地面积和领水面积共约9970000km2 , 9970000这个数用科学记数法可表示为( )A、9.97×105 B、99.7×105 C、9.97×106 D、0.997×1073. 如图是由棱长为1的正方体搭成的某几何体三视图,则图中棱长为1的正方体的个数是( )
2. 中国的陆地面积和领水面积共约9970000km2 , 9970000这个数用科学记数法可表示为( )A、9.97×105 B、99.7×105 C、9.97×106 D、0.997×1073. 如图是由棱长为1的正方体搭成的某几何体三视图,则图中棱长为1的正方体的个数是( )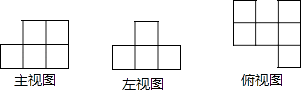 A、9 B、8 C、7 D、64. 一次函数y=﹣3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥﹣3x+b的解集在数轴上表示正确的是( )
A、9 B、8 C、7 D、64. 一次函数y=﹣3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥﹣3x+b的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、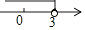 5. 某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
5. 某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.甲
乙
丙
平均数
7.9
7.9
8.0
方差
3.29
0.49
1.8
根据以上图表信息,参赛选手应选( )
 A、甲 B、乙 C、丙 D、丁6. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A、甲 B、乙 C、丙 D、丁6. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) A、45° B、50° C、55° D、60°7. 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB= ,∠C=120°,则点B′的坐标为( )
A、45° B、50° C、55° D、60°7. 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB= ,∠C=120°,则点B′的坐标为( ) A、(3,
A、(3, )
B、(3,-
)
B、(3,-  )
C、(
)
C、(  ,
,  )
D、(
)
D、(  ,-
,-  )
8.
)
8.如图,在▱ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△AOB的值为( )
 A、1:3 B、1:5 C、1:6 D、1:119. 如图,在平面直角坐标系中,抛物线y= x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为 ,则a、b的值分别为( )
A、1:3 B、1:5 C、1:6 D、1:119. 如图,在平面直角坐标系中,抛物线y= x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为 ,则a、b的值分别为( ) A、
A、 ,
B、
,
B、 ,﹣
,﹣ 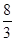 C、
C、 ,﹣
D、﹣
,﹣
D、﹣  ,
10. 在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( )
,
10. 在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017 D2017的边长是( ) A、( )2016 B、( )2017 C、( )2016 D、( )2017
A、( )2016 B、( )2017 C、( )2016 D、( )2017二、填空题
-
11. 计算: +(π﹣2)0+(﹣1)2017= .12. 已知关于x的一元二次方程ax2﹣(a+2)x+2=0有两个不相等的正整数根时,整数a的值是 .13. 如图,已知第一象限内的点A在反比例函数y= 上,第二象限的点B在反比例函数y= 上,且OA⊥OB,tanA= ,则k的值为 .
 14. 如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 .
14. 如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为 . 15. 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为 .
15. 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为 .
三、解答题
-
16. 先化简,再求值: ÷ ,其中m是方程x2+2x-3=0的根.17. 在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别
消费额(元)
A
10≤x<100
B
100≤x<200
C
20≤x<300
D
300≤x<400
E
x≥400

请结合图表中相关数据解答下列问题:
(1)、这次接受调查的有户;(2)、在扇形统计图中,“E”所对应的圆心角的度数是;(3)、请你补全频数直方图;(4)、若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?18. 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO. (1)、求证:△CDP≌△POB;(2)、填空:
(1)、求证:△CDP≌△POB;(2)、填空:①若AB=4,则四边形AOPD的最大面积为;
②连接OD,当∠PBA的度数为时,四边形BPDO是菱形.
19. 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.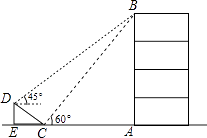 (1)、求斜坡CD的高度DE;(2)、求大楼AB的高度(结果保留根号)20. 某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。(1)、求购买一个足球、一个篮球各需多少元?(2)、根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?21. 根据下列要求,解答相关问题:(1)、请补全以下求不等式﹣2x2﹣4x≥0的解集的过程
(1)、求斜坡CD的高度DE;(2)、求大楼AB的高度(结果保留根号)20. 某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。(1)、求购买一个足球、一个篮球各需多少元?(2)、根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?21. 根据下列要求,解答相关问题:(1)、请补全以下求不等式﹣2x2﹣4x≥0的解集的过程①构造函数,画出图象:
根据不等式特征构造二次函数y=﹣2x2﹣4x;抛物线的对称轴x=﹣1,开口向下,顶点(﹣1,2)与x轴的交点是(0,0),(﹣2,0),用三点法画出二次函数y=﹣2x2﹣4x的图象如图1所示;

②数形结合,求得界点:
当y=0时,求得方程﹣2x2﹣4x=0的解为;
③借助图象,写出解集:
由图象可得不等式﹣2x2﹣4x≥0的解集为 .
(2)、利用(1)中求不等式解集的方法步骤,求不等式x2﹣2x+1<4的解集.①构造函数,画出图象;
②数形结合,求得界点;
③借助图象,写出解集.
(3)、参照以上两个求不等式解集的过程,借助一元二次方程的求根公式,直接写出关于x的不等式ax2+bx+c>0(a>0)的解集.22.
(1)、问题发现:
如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC,请判断:FG与CE的数量关系是 , 位置关系是 .
(2)、拓展探究:如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;
(3)、类比延伸:如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
23. 如图,二次函数y=ax2+bx+c的图象与x轴的交点为A、D(A在D的右侧),与y轴的交点为C,且A(4,0),C(0,﹣3),对称轴是直线x=1. (1)、求二次函数的解析式;(2)、若M是第四象限抛物线上一动点,且横坐标为m,设四边形OCMA的面积为s.请写出s与m之间的函数关系式,并求出当m为何值时,四边形OCMA的面积最大;(3)、设点B是x轴上的点,P是抛物线上的点,是否存在点P,使得以A,B、C,P四点为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、求二次函数的解析式;(2)、若M是第四象限抛物线上一动点,且横坐标为m,设四边形OCMA的面积为s.请写出s与m之间的函数关系式,并求出当m为何值时,四边形OCMA的面积最大;(3)、设点B是x轴上的点,P是抛物线上的点,是否存在点P,使得以A,B、C,P四点为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.