云南省弥勒市2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、单选题
-
1. 一种微粒的半径是0.000041米,0.000041这个数用科学记数法表示为( )A、41
 B、4.1
B、4.1  C、0. 41
C、0. 41  D、4.1
D、4.1  2. 下列计算正确的是( )A、
2. 下列计算正确的是( )A、 B、
B、 C、
C、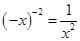 D、
D、 3. 下列说法正确的是( )A、检测某批次灯泡的使用寿命,适宜用全面调查 B、可能性是1
3. 下列说法正确的是( )A、检测某批次灯泡的使用寿命,适宜用全面调查 B、可能性是1 的事件在一次试验中一定不会发生
C、数据3,5,4,1,-2的中位数是4
D、“367人中有2人同月同日出生”为确定事件
4. 一元二次方程 的解是( )A、x1=1,x2=2 B、 x1=-1,x2=-2 C、 x1=-1,x2=-2 D、x1=-1,x2=25. 图(1)是一个横断面为抛物线形状的拱桥,当水面在图(1)位置时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
的事件在一次试验中一定不会发生
C、数据3,5,4,1,-2的中位数是4
D、“367人中有2人同月同日出生”为确定事件
4. 一元二次方程 的解是( )A、x1=1,x2=2 B、 x1=-1,x2=-2 C、 x1=-1,x2=-2 D、x1=-1,x2=25. 图(1)是一个横断面为抛物线形状的拱桥,当水面在图(1)位置时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( ) A、y=-2
A、y=-2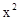 B、y=2
B、y=2 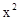 C、y= -
C、y= - 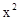 D、y=
D、y= 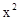 6. 下列命题错误的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、一条对角线平分一组对角的四边形是菱形 D、对角线互相垂直的矩形是正方形7. 在同一平面直角坐标系中,一次函数y=ax+c和二次函数y=a +c的大致图像是所示中的( )A、
6. 下列命题错误的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、一条对角线平分一组对角的四边形是菱形 D、对角线互相垂直的矩形是正方形7. 在同一平面直角坐标系中,一次函数y=ax+c和二次函数y=a +c的大致图像是所示中的( )A、 B、
B、 C、
C、 D、
D、 8. 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行道的宽度为x米,则可以列出关于x的方程是( )
8. 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行道的宽度为x米,则可以列出关于x的方程是( )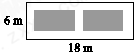 A、x2+9x-8=0 B、x2-9x-8=0 C、x2-9x+8=0 D、2x2-9x+8=0
A、x2+9x-8=0 B、x2-9x-8=0 C、x2-9x+8=0 D、2x2-9x+8=0二、填空题
-
9. 化简 的结果是 .10. 分解因式:ax2﹣ay2= .11. 如下图是一个几何体的三视图(图中尺寸单位:cm),根据图中所示数据计算这个几何体的侧面积为c .(注意:计算结果保留 )
 12. 将抛物线y=2 向右平移3个单位,再向下平移5个单位,得到的抛物线的表达式为.13. 如图,已知 为四边形 的外接圆, 为圆心,若 BCD=120 º ,AB=AD=2cm,则 的半径长为 cm.
12. 将抛物线y=2 向右平移3个单位,再向下平移5个单位,得到的抛物线的表达式为.13. 如图,已知 为四边形 的外接圆, 为圆心,若 BCD=120 º ,AB=AD=2cm,则 的半径长为 cm.
三、解答题
-
14. 计算:
|1- .
15. 如图,在△ABC和△ABD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA,求证:AC=BD. 16. 表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么 与n的关系式是:
16. 表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么 与n的关系式是:(其中,a,b是常数,n≥4)
(1)、通过画图,可得四边形时, =(填数字);五边形时, =(填数字).(2)、请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.17. 如图,在平面直角坐标系中,直线 是第一、三象限的角平分线. (1)、由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标: 、 ;(2)、结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点 关于第一、三象限的角平分线 的对称点 的坐标为(不必证明);(3)、已知两点 、 ,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.18. 九(1)班48名学生参加学校举行的“珍惜生命,远离毒品”知识竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
(1)、由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标: 、 ;(2)、结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点 关于第一、三象限的角平分线 的对称点 的坐标为(不必证明);(3)、已知两点 、 ,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.18. 九(1)班48名学生参加学校举行的“珍惜生命,远离毒品”知识竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.频数分布表
分数段
频数(人数)
16
24

请解答下列问题:
(1)、完成频数分布表, , .(2)、补全频数分布直方图;(3)、全校共有600名学生参加初赛,估计该校成绩 范围内的学生有多少人?(4)、九(1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.19. 有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润 (万元)与投资成本x(万元)满足如图①所示的二次函数 ;种植柏树的利润 (万元)与投资成本x(万元)满足如图②所示的正比例函数 =kx. (1)、分别求出利润 (万元)和利润 (万元)关于投资成本x(万元)的函数关系式;(2)、如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?20. 如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.
(1)、分别求出利润 (万元)和利润 (万元)关于投资成本x(万元)的函数关系式;(2)、如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?20. 如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN. (1)、请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(1)、请你观察图1,猜想∠MBN的度数是多少,并证明你的结论;
(2)、将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,猜测MN与BM的数量关系,无需证明.21. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.(1)、如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;(3)、如果△ABC是等边三角形,试求这个一元二次方程的根.22. 如图,抛物线 与 轴交 、 两点( 点在 点左侧),直线 与抛物线交于 、 两点,其中 点的横坐标为2.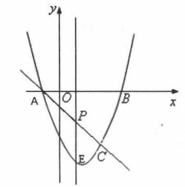 (1)、求 、 两点的坐标及直线 的函数表达式;(2)、 是线段 上的一个动点,过 点作 轴的平行线交抛物线于 点,求线段 长度的最大值;(3)、点 是抛物线上的动点,在 轴上是否存在点 ,使 、 、 、 四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的 点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.
(1)、求 、 两点的坐标及直线 的函数表达式;(2)、 是线段 上的一个动点,过 点作 轴的平行线交抛物线于 点,求线段 长度的最大值;(3)、点 是抛物线上的动点,在 轴上是否存在点 ,使 、 、 、 四个点为顶点的四边形是平行四边形?如果存在,写出所有满足条件的 点坐标(请直接写出点的坐标,不要求写过程);如果不存在,请说明理由.