云南省保山市腾冲市2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、单选题
-
1. ﹣|﹣3|的倒数是( )A、3 B、﹣3 C、 D、2. 下列计算正确的是( )A、a4+a4=2a4 B、a2·a3=a6 C、(a4)3=a7 D、a6÷a2=a33. 不等式组 的解在数轴上表示为( )A、
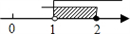 B、
B、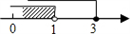 C、
C、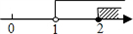 D、
D、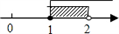 4. 关于x的一元二次方程(k–1)x2–2x+3=0有两个不相等的实数根,则k的取值范围是( )A、k< B、k< 且k≠1 C、0<k< D、k≠15. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同.小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( )A、6 B、16 C、18 D、246. 二次函数 的图像的顶点坐标是( )A、(1,8) B、(–1,8) C、(–1,2) D、(1,–4)7. 若圆锥的底面半径为3,母线长为5,则它的侧面展开图的圆心角等于( )A、108° B、144° C、180° D、216°8. 函数y= 与y=mx﹣m(m≠0)在同一平面直角坐标系中的图象可能是( )A、
4. 关于x的一元二次方程(k–1)x2–2x+3=0有两个不相等的实数根,则k的取值范围是( )A、k< B、k< 且k≠1 C、0<k< D、k≠15. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同.小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( )A、6 B、16 C、18 D、246. 二次函数 的图像的顶点坐标是( )A、(1,8) B、(–1,8) C、(–1,2) D、(1,–4)7. 若圆锥的底面半径为3,母线长为5,则它的侧面展开图的圆心角等于( )A、108° B、144° C、180° D、216°8. 函数y= 与y=mx﹣m(m≠0)在同一平面直角坐标系中的图象可能是( )A、 B、
B、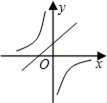 C、
C、 D、
D、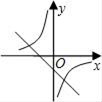
二、填空题
-
9. 小明在“百度”搜索引擎中输入“钓鱼岛最新消息”,能搜索到与之相关的结果个数约为5640000,这个数用科学记数法表示为 .10. 把多项式2x2﹣8分解因式得: .11. 样本5,4,3,2,1的方差是;标准差是;中位数是。12. 已知两圆的半径分别为1和3.若两圆相切,则两圆的圆心距为 .13. 已知点A(2,4)与点B(b–1,2a)关于原点对称,则a= , b= .14. 函数 中自变量 的取值范围是.
三、解答题
-
15. 计算: .16. 先化简 ,然后从 ,1,-1中选取一个你认为合适的数作为x的值代入求值.17. 如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
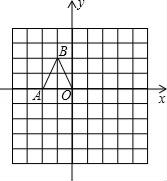 (1)、以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2:1,画出△OA1B1 . (所画△OA1B1与△OAB在原点两侧);(2)、求出线段A1B1所在直线的函数关系式.18. 为迎接国庆60周年,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
(1)、以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2:1,画出△OA1B1 . (所画△OA1B1与△OAB在原点两侧);(2)、求出线段A1B1所在直线的函数关系式.18. 为迎接国庆60周年,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:分数段
频数
频率
60≤x<70
30
0.15
70≤x<80
m
0.45
80≤x<90
60
n
90≤x<100
20
0.1
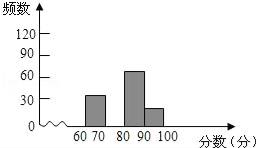
请根据以上图表提供的信息,解答下列问题:
(1)、表中m和n所表示的数分别为:m= , n=;(2)、请在图中,补全频数分布直方图;(3)、比赛成绩的中位数落在哪个分数段;(4)、如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?19. 如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.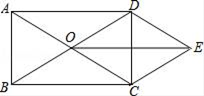 (1)、求证:OE⊥DC.(2)、若∠AOD=120°,DE=2,求矩形ABCD的面积.20. 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)、求证:OE⊥DC.(2)、若∠AOD=120°,DE=2,求矩形ABCD的面积.20. 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.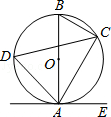 (1)、求∠ABC的度数;(2)、求证:AE是⊙O的切线;(3)、当BC=4时,求劣弧AC的长.21. 为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8 mg.根据以上信息,解答下列问题:
(1)、求∠ABC的度数;(2)、求证:AE是⊙O的切线;(3)、当BC=4时,求劣弧AC的长.21. 为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8 mg.根据以上信息,解答下列问题: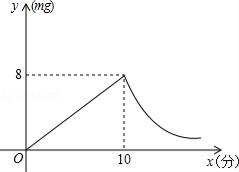 (1)、求药物燃烧时y与x的函数关系式;(2)、求药物燃烧后y与x的函数关系式;(3)、当每立方米空气中含药量低于1.6 mg时,对人体无毒害作用.那么从消毒开始,经多长时间学生才可以返回教室?22. 某商场以每件20元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足关系:m=140﹣2x.(1)、写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式;(2)、如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?23. 在平面直角坐标系中,已知抛物线y=ax2+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)、求药物燃烧时y与x的函数关系式;(2)、求药物燃烧后y与x的函数关系式;(3)、当每立方米空气中含药量低于1.6 mg时,对人体无毒害作用.那么从消毒开始,经多长时间学生才可以返回教室?22. 某商场以每件20元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足关系:m=140﹣2x.(1)、写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式;(2)、如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?23. 在平面直角坐标系中,已知抛物线y=ax2+bx﹣4经过A(﹣4,0),C(2,0)两点.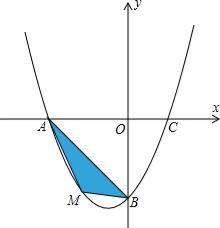 (1)、求抛物线的解析式;(2)、若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;(3)、若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
(1)、求抛物线的解析式;(2)、若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;(3)、若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.