云南省昭通市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、单选题
-
1. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 用配方法解方程x2+2x﹣3=0,下列配方结果正确的是( )A、(x﹣1)2=2 B、(x﹣1)2=4 C、(x+1)2=2 D、(x+1)2=43. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
2. 用配方法解方程x2+2x﹣3=0,下列配方结果正确的是( )A、(x﹣1)2=2 B、(x﹣1)2=4 C、(x+1)2=2 D、(x+1)2=43. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A、 B、
B、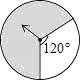 C、
C、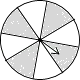 D、
D、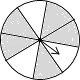 4. 函数y=(m+2) +2x+1是二次函数,则m的值为( )A、﹣2 B、0 C、﹣2或1 D、15. 如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( )
4. 函数y=(m+2) +2x+1是二次函数,则m的值为( )A、﹣2 B、0 C、﹣2或1 D、15. 如图,已知⊙O的直径AE=10cm,∠B=∠EAC,则AC的长为( )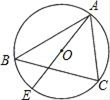 A、5cm B、5 cm C、5 cm D、6cm6. 某机械厂七月份生产零件50万个,第三季度生产零件182万个.若该厂八、九月份平均每月生产零件的增长率均为x,则下面所列方程正确的是( )A、50(1+x)2=182 B、50+50(1+x)2=182 C、50+50(1+x)+50(1+2x)=182 D、50+50(1+x)+50(1+x)2=1827. 已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为 的是( )A、
A、5cm B、5 cm C、5 cm D、6cm6. 某机械厂七月份生产零件50万个,第三季度生产零件182万个.若该厂八、九月份平均每月生产零件的增长率均为x,则下面所列方程正确的是( )A、50(1+x)2=182 B、50+50(1+x)2=182 C、50+50(1+x)+50(1+2x)=182 D、50+50(1+x)+50(1+x)2=1827. 已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为 的是( )A、 B、
B、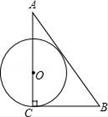 C、
C、 D、
D、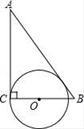 8. 若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
8. 若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A、抛物线开口向下 B、抛物线与x轴的交点为(﹣1,0),(3,0) C、当x=1时,y有最大值为0 D、抛物线的对称轴是直线x=9. 下列图形中,关于直线l对称的是( )A、 B、
B、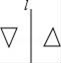 C、
C、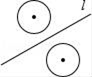 D、
D、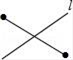 10. 下列长度的三条线段能组成三角形的一组是( )A、1,2,3 B、4,5,9 C、4,6,8 D、5,5,1111. 若分式 有意义,则x的取值范围是( )A、x≠﹣3 B、x≥﹣3 C、x≠﹣3且 x≠2 D、x≠212. 下列计算正确的是( )A、a•a2=a2 B、(a2)2=a4 C、3a+2a=5a2 D、(a2b)3=a2•b313. 下列各式由左边到右边的变形中,是分解因式的为( )A、a(x+y)=ax+ay B、x2﹣4x+4=x(x﹣4)+4 C、x2﹣16+3x=(x+4)(x﹣4)+3x D、10x2﹣5x=5x(2x﹣1)14. 有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积( )
10. 下列长度的三条线段能组成三角形的一组是( )A、1,2,3 B、4,5,9 C、4,6,8 D、5,5,1111. 若分式 有意义,则x的取值范围是( )A、x≠﹣3 B、x≥﹣3 C、x≠﹣3且 x≠2 D、x≠212. 下列计算正确的是( )A、a•a2=a2 B、(a2)2=a4 C、3a+2a=5a2 D、(a2b)3=a2•b313. 下列各式由左边到右边的变形中,是分解因式的为( )A、a(x+y)=ax+ay B、x2﹣4x+4=x(x﹣4)+4 C、x2﹣16+3x=(x+4)(x﹣4)+3x D、10x2﹣5x=5x(2x﹣1)14. 有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积( )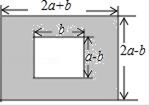 A、4a2 B、4a2﹣ab C、4a2+ab D、4a2﹣ab﹣2b215. 如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )
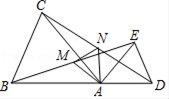
A、4a2 B、4a2﹣ab C、4a2+ab D、4a2﹣ab﹣2b215. 如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )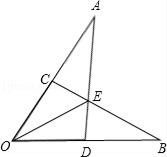 A、2对 B、3对 C、4对 D、5对16. 如图AD⊥BC,D为BC的中点,以下结论正确的有( )个
A、2对 B、3对 C、4对 D、5对16. 如图AD⊥BC,D为BC的中点,以下结论正确的有( )个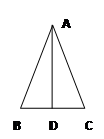
①△ABD≌△ACD ②AB=AC ③∠B=∠C ④AD是△ABC的角平分线。
A、1 B、2 C、3 D、4二、填空题
-
17. 下列事件:①打开电视机,它正在播广告;②从一只装有红球的口袋中,任意摸出一个球,恰是白球;③两次抛掷正方体骰子,掷得的数字之和<13;④抛掷硬币 1000 次,第 1000 次正面向上,其中为随机事件的有个.18. 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为 .
 19. 一元二次方程2x2﹣4x+1=0有个实数根.20. 为响应“足球进校园”的号召,我县教体局在今年 11 月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度 h(m)可用公式 h=﹣5t2+v0t 表示,其中 t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到 20m,那么足球被踢出时的速度应达到m/s.21. 已知圆锥的底面半径为3,母线长为6,则此圆锥侧面展开图的圆心角是 .22. 为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB,AC夹角为120°,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为cm2 .
19. 一元二次方程2x2﹣4x+1=0有个实数根.20. 为响应“足球进校园”的号召,我县教体局在今年 11 月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度 h(m)可用公式 h=﹣5t2+v0t 表示,其中 t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到 20m,那么足球被踢出时的速度应达到m/s.21. 已知圆锥的底面半径为3,母线长为6,则此圆锥侧面展开图的圆心角是 .22. 为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB,AC夹角为120°,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为cm2 .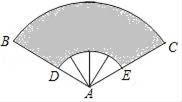 23. 计算: = .24. 计算:(﹣2ab2)3÷4a2b2= .25. 已知:在一个直角三角形中30°角所对的直角边为3cm,则斜边长为 .26. 如图,△ACB≌△A′CB′,∠BCB′=37°,则∠ACA′的度数为 .
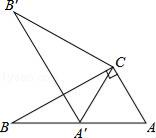
23. 计算: = .24. 计算:(﹣2ab2)3÷4a2b2= .25. 已知:在一个直角三角形中30°角所对的直角边为3cm,则斜边长为 .26. 如图,△ACB≌△A′CB′,∠BCB′=37°,则∠ACA′的度数为 . 27. 已知一个多边形的内角和为540°,则这个多边形是边形.28. 如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 , P2 , 连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2= .
27. 已知一个多边形的内角和为540°,则这个多边形是边形.28. 如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1 , P2 , 连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2= .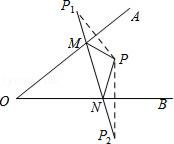
三、解答题
-
29.(1)、解方程:x(x﹣2)+x﹣2=0;(2)、用配方法解方程:x2﹣10x+22=030.(1)、请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标.
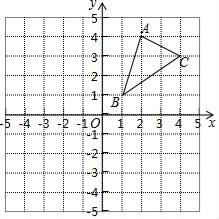 (2)、请画出△ABC绕点B逆时针旋转90°后的△A2BC2 .(3)、求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).31. 一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.
(2)、请画出△ABC绕点B逆时针旋转90°后的△A2BC2 .(3)、求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).31. 一个盒中有4个完全相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球然后放回,再随机摸出一个小球.(Ⅰ)请用列表法(或画树状图法)列出所有可能的结果;
(Ⅱ)求两次取出的小球标号相同的概率;
(Ⅲ)求两次取出的小球标号的和大于6的概率.
32. 在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c). (1)、当c=﹣3时,点(x1 , y1)在抛物线y=x2﹣2x+c上,求y1的最小值;(2)、若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA= OB,求抛物线的解析式;(3)、当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.33. 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2 , 那么通道的宽应设计成多少m?
(1)、当c=﹣3时,点(x1 , y1)在抛物线y=x2﹣2x+c上,求y1的最小值;(2)、若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA= OB,求抛物线的解析式;(3)、当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.33. 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2 , 那么通道的宽应设计成多少m?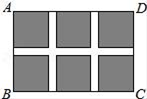 34. 已知,如图:AB为⊙O直径,D为弧AC中点,DE⊥AB于E,AC交OD于点F,
34. 已知,如图:AB为⊙O直径,D为弧AC中点,DE⊥AB于E,AC交OD于点F,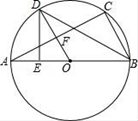 (1)、求证:OD∥BC;(2)、若AB=10cm,BC=6cm,求DF的长;(3)、探索DE与AC的数量关系,直接写出结论不用证明.35. 某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.(1)、求y与x的函数关系式,并直接写出自变量x的取值范围;(2)、每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?(3)、每件商品的售价定为多少元时,每周的利润恰好是2145元?36. 已知△ABC内接于⊙O,过点A作直线EF.(1)、如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(1)、求证:OD∥BC;(2)、若AB=10cm,BC=6cm,求DF的长;(3)、探索DE与AC的数量关系,直接写出结论不用证明.35. 某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.(1)、求y与x的函数关系式,并直接写出自变量x的取值范围;(2)、每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?(3)、每件商品的售价定为多少元时,每周的利润恰好是2145元?36. 已知△ABC内接于⊙O,过点A作直线EF.(1)、如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).(ī)(īī)(īīī)
(2)、如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?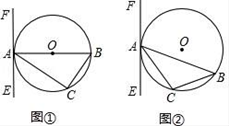 37. 已知,抛物线y=mx2+(1﹣2m)x+1﹣3m(m是常数).
37. 已知,抛物线y=mx2+(1﹣2m)x+1﹣3m(m是常数).(Ⅰ)当m=1时,求该抛物线与x轴的公共点的坐标;
(Ⅱ)抛物线与x轴相交于不同的两点A,B.
①求m的取值范围;
②无论m取何值,该抛物线都经过非坐标轴上的定点P,当 <m≤8时,求△PAB面积的最大值,并求出相对应的m的值.
38.(1)、化简(2x+y)2﹣4(x+ y)(x﹣ y);(2)、解方程: =0;(3)、分解因式:ax2﹣2a2x+a3 .39. 如图,AD平分∠BAC,其中∠B=35°,∠ADC=82°,求∠BAC,∠C的度数.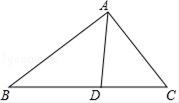 40. 如图,点B,D,C,F在同一条直线上,∠A=∠E,AB=EF,∠B=∠F.求证:BD=CF.
40. 如图,点B,D,C,F在同一条直线上,∠A=∠E,AB=EF,∠B=∠F.求证:BD=CF.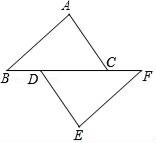 41. 先化简,再求值:( )÷ ,其中x=﹣1.42. 某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少要答对多少道题?43. 甲、乙两地相距240千米,一辆小轿车的速度是货车速度的2倍,走完全程,小轿车比货车少用2小时,求小轿车的速度.44. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(1,3),B(﹣2,﹣2),C(2,﹣1).
41. 先化简,再求值:( )÷ ,其中x=﹣1.42. 某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,小明得分要超过90分,他至少要答对多少道题?43. 甲、乙两地相距240千米,一辆小轿车的速度是货车速度的2倍,走完全程,小轿车比货车少用2小时,求小轿车的速度.44. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(1,3),B(﹣2,﹣2),C(2,﹣1). (1)、画出△ABC关于y轴对称的△A1B1C1;(2)、写出点A1 , B1 , C1的坐标;(3)、求△ABC的面积.
(1)、画出△ABC关于y轴对称的△A1B1C1;(2)、写出点A1 , B1 , C1的坐标;(3)、求△ABC的面积.