2018-2019学年初中数学浙教版八年级下册第二章一元二次方程单元检测卷a
试卷更新日期:2019-03-26 类型:单元试卷
一、选择题
-
1. 下列方程中,是关于x的一元二次方程的是( )A、x2+3y=1 B、x2+3x=1 C、ax2+bx+c=0 D、
 2. 关于x的一元二次方程: 有两个实数根x1、x2,则 =( )
2. 关于x的一元二次方程: 有两个实数根x1、x2,则 =( )
A、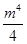 B、
B、 C、4
D、﹣4
3. 已知 ,则 的值是( )A、-3 B、4 C、-3或4 D、3或-44. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断5. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )A、80(1+x)2=100 B、100(1﹣x)2=80 C、80(1+2x)=100 D、80(1+x2)=1006. 若方程式 根均为正数,其中c为整数,则c的最小值为何?( )
C、4
D、﹣4
3. 已知 ,则 的值是( )A、-3 B、4 C、-3或4 D、3或-44. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断5. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )A、80(1+x)2=100 B、100(1﹣x)2=80 C、80(1+2x)=100 D、80(1+x2)=1006. 若方程式 根均为正数,其中c为整数,则c的最小值为何?( )
A、1 B、8 C、16 D、617. 设a、b是方程x2+x﹣2014=0的两个实数根,则a2+2a+b的值为( )A、2014 B、2015 C、2012 D、20138. 鸡瘟是一种传播速度很强的传染病,一轮传染为一天时间,红发养鸡场于某日发现一例,两天后发现共有169只鸡患有这种病.若每例病鸡传染健康鸡的只数均相同,则每只病鸡传染健康鸡的只数为( )
A、10只 B、11只 C、12只 D、13只9. 设x1 , x2是方程 的两个实数根,则
A、2016 B、2017 C、2018 D、201910. 方程(x﹣3)(x﹣9)=0的根是 .11. 关于x的一元二次方程x2+bx+2=0有两个不相等的实数根,写出一个满足条件的实数b的值:b= .12. 已知关于 x的一元二次方程 的一个根为0 ,则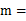 .
.
13. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有两个不相等的实数根,则k的取值范围是14. 通过学习,爱好思考的小明发现,一元二次方程的根完全由它的系数确定,即一元二次方程ax2+bx+c=0(a≠0),当b2﹣4ac≥0时有两个实数根:x1= ,x2= ,于是:x1+x2= ,x1•x2= 、这就是著名的韦达定理.请你运用上述结论解决下列问题:关于x的一元二次方程x2+kx+k+1=0的两实数根分别为x1 , x2 , 且x12+x22=1,则k的值为 .15. 将一些相同的“○”按如图所示的规律依次摆放,观察每个“龟图”中的“○”的个数,若第n个“龟图”中有245个“○”,则n= . 16. 关于x的一元二次方程x(x﹣2)=﹣x﹣2①与一元一次方程2x+1=2a﹣x②.
16. 关于x的一元二次方程x(x﹣2)=﹣x﹣2①与一元一次方程2x+1=2a﹣x②.
(1)、若方程①的一个根是方程②的根,求a的值;
(2)、若方程②的根不小于方程①两根中的较小根且不大于方程①两根中的较大根,求a的取值范围.
17. 有一个三角形,面积为30cm2 , 其中一边比这边上的高的4倍少1cm. 若设这边上的高为xcm,请你列出关于x的方程,并判断它是什么方程?若是一元二次方程,把它化为一般形式,并指出二次项系数、一次项系数和常数项.18. 已知关于x的方程(m+1) +(m-2)x-1=0.(1)、m取何值时,它是一元二次方程?并写出这个方程的解;(2)、m取何值时,它是一元一次方程?19. 解方程:
(1)、(x+8)2=36;(2)、x(5x+4)-(4+5x)=0;(3)、x2+3=3(x+1);
(4)、2x2-x-1=0.
20. 已知关于x的方程x2﹣mx﹣8=0.(1)、当m=2时,求方程的根;(2)、设原方程的两个根是x1、x2 , 若x12+x22﹣4x1x2=97,求m的值.21. 收发微信红包已成为各类人群进行交流联系,增强感情的一部分,下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话.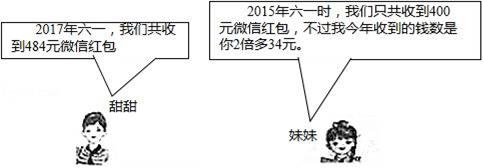
请问:
(1)、2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少?(2)、2017年六一甜甜和她妹妹各收到了多少钱的微信红包?22. 某地大力发展经济作物,其中果树种植已初具规模,今年受气候、雨水等因素的影响,樱桃较去年有小幅度的减产,而枇杷有所增产.(1)、该地某果农今年收获樱桃和枇杷共400千克,其中枇杷的产量不超过樱桃产量的7倍,求该果农今年收获樱桃至少多少千克?(2)、该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售,该果农去年樱桃的市场销售量为100千克,销售均价为30元/千克,今年樱桃的市场销售量比去年减少了m%,销售均价与去年相同,该果农去年枇杷的市场销售量为200千克,销售均价为20元/千克,今年枇杷的市场销售量比去年增加了2m%,但销售均价比去年减少了m%,该果农今年运往市场销售的这部分樱桃和枇杷的销售总金额比他去年樱桃和枇杷的市场销售总金额相同,求m的值.23. 已知在关于x的分式方程 ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.(1)、求k的取值范围;(2)、当方程②有两个整数根x1、x2 , k为整数,且k=m+2,n=1时,求方程②的整数根;(3)、当方程②有两个实数根x1、x2 , 满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.