浙江省杭州市萧山区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、单选题
-
1. 一个数的相反数是它本身,则这个数是( )A、0 B、正数 C、负数 D、非负数2. 总投资约为42.5亿元,以打造美丽生态带、休闲旅游带、运动健身带和南部绿色带为目标的萧山区浦阳江治理工程已见成效,则42.5亿元用科学记数法可表示为( )A、
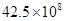 B、
B、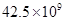 C、
C、 D、
D、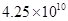 3. 用代数式表示“ 的和除以 所得的商”( )A、
3. 用代数式表示“ 的和除以 所得的商”( )A、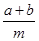 B、
B、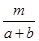 C、
C、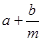 D、
D、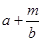 4. 下列各数中,结果是负数的是( )A、
4. 下列各数中,结果是负数的是( )A、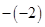 B、
C、
B、
C、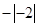 D、
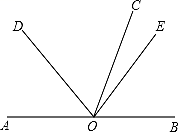
D、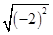 5. 如图:A,B,C,D四点在一条直线上,若AB=CD,下列各式表示线段AC不正确的是( )
5. 如图:A,B,C,D四点在一条直线上,若AB=CD,下列各式表示线段AC不正确的是( ) A、AC=AD﹣CD B、AC=AB+BC C、AC=BD﹣AB D、AC=AD﹣AB6. 长、宽、高分别为 的长方形箱子按如图方式打包(粗黑线),则打包带的长至少为( )
A、AC=AD﹣CD B、AC=AB+BC C、AC=BD﹣AB D、AC=AD﹣AB6. 长、宽、高分别为 的长方形箱子按如图方式打包(粗黑线),则打包带的长至少为( )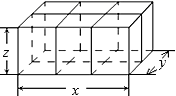 A、
A、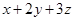 B、
B、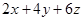 C、
C、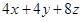 D、
D、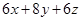 7. 下列各式变形正确的是( )A、由
7. 下列各式变形正确的是( )A、由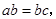 得
B、由
得
B、由 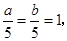 得
得 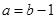 C、由
C、由 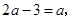 得
D、由 2a-1=3a+1, 得 a=2
8. 下列计算错误的是( )A、
得
D、由 2a-1=3a+1, 得 a=2
8. 下列计算错误的是( )A、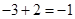 B、
B、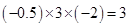 C、
C、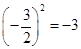 D、
D、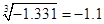 9. A,B两地相距720km,甲车从A地出发前往B地,行驶120km后,乙车从B地驶往A地,3h后两车相遇,若乙车速度是甲车速度的 倍,设甲车的速度为 则可列方程( )
9. A,B两地相距720km,甲车从A地出发前往B地,行驶120km后,乙车从B地驶往A地,3h后两车相遇,若乙车速度是甲车速度的 倍,设甲车的速度为 则可列方程( )
A、 B、
B、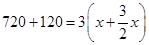 C、
C、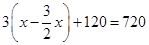 D、
D、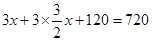 10. 如图示一副特制的三角板,用它们可以画出一些特殊角,在下列选项中,不能画出的角度是( )
10. 如图示一副特制的三角板,用它们可以画出一些特殊角,在下列选项中,不能画出的角度是( )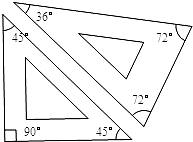 A、18° B、55° C、63° D、117°
A、18° B、55° C、63° D、117°二、填空题
-
11. 当 时, 的值为.12. 有理数 在数轴上对应点的位置如图所示,若有理数 互为相反数,则这四个数有理数中,绝对值最大的是.
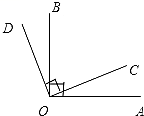
 13. 已知 则 可取的整数值为.14. 如图,射线OA⊥OB,射线OC⊥OD,试说明∠AOC=∠BOD的理由.
13. 已知 则 可取的整数值为.14. 如图,射线OA⊥OB,射线OC⊥OD,试说明∠AOC=∠BOD的理由.解:∵OA⊥OB,OC⊥OD
∴∠AOB=∠COD=°(垂直的定义)
即∠AOC+∠BOC=∠BOD+
∴∠AOC=∠BOD()
 15. 对于计算,我们要观察计算对象,明确运算顺序,选择运算律,利用运算法则进行正确的计算,请完成下列填空:16. 我们规定:若关于 的一元一次方程 的解为 则称该方程为“和解方程”,例如:方程 的解为 而-2=-4+2,则方程 为“和解方程”.
15. 对于计算,我们要观察计算对象,明确运算顺序,选择运算律,利用运算法则进行正确的计算,请完成下列填空:16. 我们规定:若关于 的一元一次方程 的解为 则称该方程为“和解方程”,例如:方程 的解为 而-2=-4+2,则方程 为“和解方程”.( 1 )若关于 的一元一次方程 是“和解方程”,则 的值为;
三、解答题
-
17. 计算(1)、(2)、18. 已知数轴上点A和点B分别位于原点O两侧,点A对应的数为 点B对应的数为 且AB=9.(1)、若 直接写出 的值;(2)、若C为AB的中点,对应的数为 且OA=2OB,求 的值.19. 如图,已知点A、B、C、D,根据下列语句画图(保留画图痕迹):
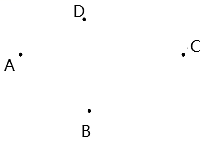 (1)、画射线AC;(2)、连接AB、BC、BD,线段BD与射线AC交于点O;(3)、①在线段AC上作一条线段CF,使得
(1)、画射线AC;(2)、连接AB、BC、BD,线段BD与射线AC交于点O;(3)、①在线段AC上作一条线段CF,使得②观察图形,我们发现线段AB+BC>AC,得出这个结论的依据是.
20. 计算(1)、(2)、