浙江省嘉兴市秀洲区三校教研共同体2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、单选题
-
1. 已知 ,则 的值为( )A、2 B、 C、 D、2. 下列事件中,不可能事件是( )A、今年的除夕夜会下雪 B、在只装有红球的袋子里摸出一个黑球 C、射击运动员射击一次,命中10环 D、任意掷一枚硬币,正面朝上3. 已知⊙O的半径r=3,PO= ,则点P与⊙O的位置关系是( )
A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、不能确定4. 对于二次函数y=2(x﹣1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线x=﹣1 C、顶点坐标是(1,2) D、与x轴有两个交点.5. 如图,点G是△ABC的重心,下列结论中正确的个数有( )① ;② ;③△EDG∽△CBG;④ .
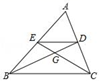 A、1个 B、2个 C、3个 D、4个6. 数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )
A、1个 B、2个 C、3个 D、4个6. 数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( ) A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径7. 将抛物线y=x2﹣2x﹣3的图象先向右平移1个单位,再向下平移4个单位,所得图象的函数解析式为( )A、y=x2﹣3x﹣7 B、y=x2﹣x﹣7 C、y=x2﹣3x+1 D、y=x2﹣4x﹣48. 如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径7. 将抛物线y=x2﹣2x﹣3的图象先向右平移1个单位,再向下平移4个单位,所得图象的函数解析式为( )A、y=x2﹣3x﹣7 B、y=x2﹣x﹣7 C、y=x2﹣3x+1 D、y=x2﹣4x﹣48. 如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.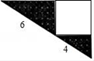 A、3 B、9 C、12 D、249. 给出下列命题及函数y=x,y=x2和y= 的图象.(如图所示)①如果 >a>a2 , 那么0<a<1;②如果a2>a> ,那么a>1;③如果a2> >a,那么a<﹣1.则真命题的个数是( )
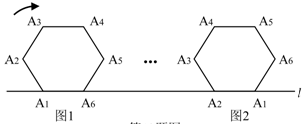
A、3 B、9 C、12 D、249. 给出下列命题及函数y=x,y=x2和y= 的图象.(如图所示)①如果 >a>a2 , 那么0<a<1;②如果a2>a> ,那么a>1;③如果a2> >a,那么a<﹣1.则真命题的个数是( )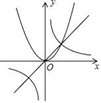 A、0 B、1 C、2 D、310. 如图,将边长为 的正六边形A1A2A3A4A5A6在直线 上由图1的位置按顺时针
A、0 B、1 C、2 D、310. 如图,将边长为 的正六边形A1A2A3A4A5A6在直线 上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的
长为( ).
 A、
A、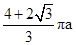 B、
B、 C、
C、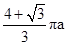 D、
D、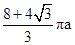
二、填空题
-
11. 已知线段a=4,线段b=9,则a,b的比例中项是 .12. 正五边形的一个内角的度数是13. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么AP的长度为cm.
 14. 如图,AB是⊙O的直径,点C、D在圆上,∠D=65°,则∠BAC等于度.
14. 如图,AB是⊙O的直径,点C、D在圆上,∠D=65°,则∠BAC等于度.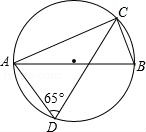 15. 如图,点D在△ABC的边AC上,若要使△ABD与△ACB相似,可添加的一个条件是(只需写出一个).
15. 如图,点D在△ABC的边AC上,若要使△ABD与△ACB相似,可添加的一个条件是(只需写出一个).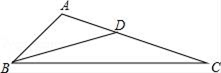 16. 在线段、等边三角形、平行四边形、圆中任意抽取两个图形,抽到的既是中心对称图形又是轴对称图形的概率是 .17. 王江泾是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为m.
16. 在线段、等边三角形、平行四边形、圆中任意抽取两个图形,抽到的既是中心对称图形又是轴对称图形的概率是 .17. 王江泾是著名的水乡,如图,圆拱桥的拱顶到水面的距离CD为9m,水面宽AB为6m,则桥拱半径OC为m. 18. 如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成一个矩形零件,使矩形PQMN的一边在BC上,其余两个顶点分别在AB、AC上.设PQ=xcm,矩形PQMN的面积为ycm2 , 请写出y关于x的函数表达式(并注明x的取值范围) .
18. 如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成一个矩形零件,使矩形PQMN的一边在BC上,其余两个顶点分别在AB、AC上.设PQ=xcm,矩形PQMN的面积为ycm2 , 请写出y关于x的函数表达式(并注明x的取值范围) .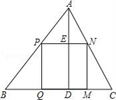 19. 如图,扇形AOB的圆心角是为90°,四边形OCDE是边长为1的正方形,点C,E,D 分别在OA,OB, 上,过A作AF⊥ED交ED的延长线于点F,那么图中阴影部分的面积为 .
19. 如图,扇形AOB的圆心角是为90°,四边形OCDE是边长为1的正方形,点C,E,D 分别在OA,OB, 上,过A作AF⊥ED交ED的延长线于点F,那么图中阴影部分的面积为 .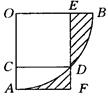 20. 如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,则AF的最小值是 .
20. 如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,则AF的最小值是 .
三、解答题
-
21. 已知二次函数y=x2+3x+m的图象与x轴交于点A(﹣4,0).(1)、求m的值;(2)、求该函数图象与坐标轴其余交点的坐标.22. 现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.

(1)、直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;(2)、求小丽投放的两袋垃圾不同类的概率.
23. 如图,△ABC内接于⊙O,AB=AC,D在弧AB上,连CD交AB于点E,B是弧CD的中点,求证:∠B=∠BEC.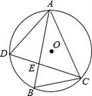 24. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C1处,点D落在点D1处,C1D1交线段AE于点G.
24. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C1处,点D落在点D1处,C1D1交线段AE于点G.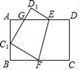
(1)、求证:△BC1F∽△AGC1;(2)、若C1是AB的中点,AB=6,BC=9,求AG的长.
25. 2015年12月16﹣18日,第二届互联网大会在浙江乌镇胜利举行,这说明我国互联网发展走到了世界的前列,尤其是电子商务.据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.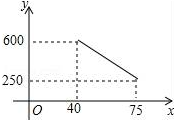 (1)、当销售单价定为50元时,求每月的销售件数;(2)、设每月获得利润为w(元),求每月获得利润w(元)关于销售单价x(元)的函数解析式;(3)、由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量)26. 如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线交抛物线于点Q,交直线BD于点M.
(1)、当销售单价定为50元时,求每月的销售件数;(2)、设每月获得利润为w(元),求每月获得利润w(元)关于销售单价x(元)的函数解析式;(3)、由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量)26. 如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线交抛物线于点Q,交直线BD于点M.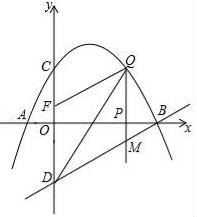 (1)、求该抛物线所表示的二次函数的表达式;(2)、点P在线段AB上运动的过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.(3)、已知点F(0, ),点P在x轴上运动,试求当m为何值时以D、M、Q、F为顶点的四边形是平行四边形.
(1)、求该抛物线所表示的二次函数的表达式;(2)、点P在线段AB上运动的过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.(3)、已知点F(0, ),点P在x轴上运动,试求当m为何值时以D、M、Q、F为顶点的四边形是平行四边形.