浙江省嘉兴市秀洲区三校教研共同体2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、单选题
-
1. 下列“表情图”中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 由下列长度的三条线段能组成三角形的是( )A、1cm,2cm,3cm B、3cm,4cm,5cm C、5cm,15cm,8cm D、6cm,8cm,1cm3. 一元一次不等式组 的解集在数轴上表示正确的是( )A、
2. 由下列长度的三条线段能组成三角形的是( )A、1cm,2cm,3cm B、3cm,4cm,5cm C、5cm,15cm,8cm D、6cm,8cm,1cm3. 一元一次不等式组 的解集在数轴上表示正确的是( )A、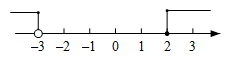
B、
B、 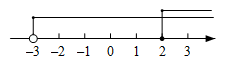
C、
C、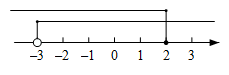
D、
D、
4. 在下列各组条件中,不能说明△ABC≌△DEF的是( )A、AB=DE,∠B=∠E,∠C=∠F B、AC=DF,BC=EF,∠A=∠D C、AB=DE,∠A=∠D,∠B=∠E D、AB=DE,BC=EF,AC=DF5. 若x轴上的点P到y轴的距离为2,则点P的坐标为( )A、(2,0) B、(2,0)或(﹣2,0) C、(0,2) D、(0,2)或(0,﹣2)6. 工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB 的边OA,OB 上分别取 OM=ON, 然后移动角尺使角尺的两边相同的刻度分别与 M,N 重合,得到∠AOB 的平分线 OP, 做法中用到三角形全等的判定方法是( )
4. 在下列各组条件中,不能说明△ABC≌△DEF的是( )A、AB=DE,∠B=∠E,∠C=∠F B、AC=DF,BC=EF,∠A=∠D C、AB=DE,∠A=∠D,∠B=∠E D、AB=DE,BC=EF,AC=DF5. 若x轴上的点P到y轴的距离为2,则点P的坐标为( )A、(2,0) B、(2,0)或(﹣2,0) C、(0,2) D、(0,2)或(0,﹣2)6. 工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB 的边OA,OB 上分别取 OM=ON, 然后移动角尺使角尺的两边相同的刻度分别与 M,N 重合,得到∠AOB 的平分线 OP, 做法中用到三角形全等的判定方法是( )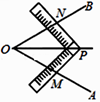 A、SSS B、SAS C、ASA D、AAS7. 已知下列命题:①若|a|=|b|,则a2=b2;②若am2>bm2 , 则a>b;③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )A、1 B、2 C、3 D、48. 将直线y=2x向右平移2个单位,再向上移动4个单位,所得的直线的解析式是( )A、y=2x B、y=2x+2 C、y=2x﹣4 D、y=2x+49. 观察图,可以得出不等式组 的解集是( )
A、SSS B、SAS C、ASA D、AAS7. 已知下列命题:①若|a|=|b|,则a2=b2;②若am2>bm2 , 则a>b;③对顶角相等;④等腰三角形的两底角相等.其中原命题和逆命题均为真命题的个数是( )A、1 B、2 C、3 D、48. 将直线y=2x向右平移2个单位,再向上移动4个单位,所得的直线的解析式是( )A、y=2x B、y=2x+2 C、y=2x﹣4 D、y=2x+49. 观察图,可以得出不等式组 的解集是( )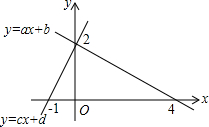 A、x<4 B、x<-1 C、-1<x<0 D、-1<x<410. 如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( )
A、x<4 B、x<-1 C、-1<x<0 D、-1<x<410. 如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( )①△ABC是等腰三角形;②BF=AC;③BH:BD:BC=1: : ;④GE2+CE2=BG2 .
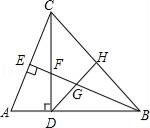 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 一个等腰三角形的一个底角为40°,则它的顶角的度数是.12. 请用不等式表示“x的2倍与3的和不大于1”: .13. 写出一个过点(0,0)且函数值y随自变量x的增大而减小的一次函数关系式 .14. 直角坐标系内点P(﹣2,3)关于x轴的对称点Q的坐标为 .15. 若点(﹣1,y1).与(2,y2)在一次函数y=﹣2x+1的图象上,则y1y2(填>、<或=).16. 如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的大小是 。
 17. 若直角三角形斜边上的高和中线长分别是3cm,4cm,则它的面积是cm2 .18. 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′= .
17. 若直角三角形斜边上的高和中线长分别是3cm,4cm,则它的面积是cm2 .18. 如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′= .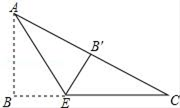 19. 直线y=k1x+b与直线y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于X的不等式 k1x+b>k2x+c的解集为 .
19. 直线y=k1x+b与直线y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于X的不等式 k1x+b>k2x+c的解集为 .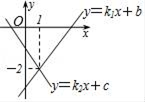 20. 如图,已知正方形ABCD的边长是2厘米,E是CD边的中点,F在BC边上移动,当AE恰好平分∠FAD时,CF=厘米.
20. 如图,已知正方形ABCD的边长是2厘米,E是CD边的中点,F在BC边上移动,当AE恰好平分∠FAD时,CF=厘米.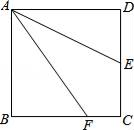
三、解答题
-
21. 解不等式(组):(1)、9x﹣2≤7x+3(2)、 .22. 已知y是x的一次函数,且当x=0时,y=﹣4;且图象通过点(1,﹣2)(1)、求这个一次函数的解析式;(2)、判断点(a,2a﹣4)是否在该函数图象上,并说明理由.23. 图l、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.点A和点B在小正方形的顶点上.
 (1)、在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个 即可);(2)、在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可);24. 如图,在△ABC中,AB=2AC,AD平分∠BAC且AD=BD.求证:CD⊥AC
(1)、在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个 即可);(2)、在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可);24. 如图,在△ABC中,AB=2AC,AD平分∠BAC且AD=BD.求证:CD⊥AC 25. 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系如图中线段AB所示,慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系如图中线段OC所示.根据图像进行以下研究:
25. 一列快车由甲地开往乙地,一列慢车由乙地开往甲地,两车同时出发,匀速运动.快车离乙地的路程y1(km)与行驶的时间x(h)之间的函数关系如图中线段AB所示,慢车离乙地的路程y2(km)与行驶的时间x(h)之间的函数关系如图中线段OC所示.根据图像进行以下研究: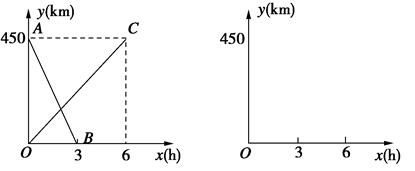 (1)、甲、乙两地之间的距离为km;(2)、线段AB的表达式为 , 线段OC的表达式为;(3)、设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数表达式,并画出函数的图象.26. 如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC= ,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
(1)、甲、乙两地之间的距离为km;(2)、线段AB的表达式为 , 线段OC的表达式为;(3)、设快、慢车之间的距离为y(km),求y与慢车行驶时间x(h)的函数表达式,并画出函数的图象.26. 如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC= ,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.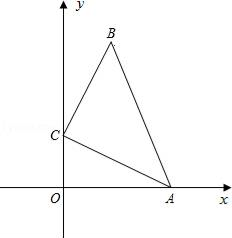 (1)、当AB∥y轴时,求B点坐标.(2)、随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标.(3)、在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是4?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.
(1)、当AB∥y轴时,求B点坐标.(2)、随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标.(3)、在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是4?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.