广西桂林市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、单选题
-
1. 下列实数中,无理数是( )A、
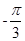 B、
C、0
D、
B、
C、0
D、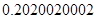 2. 下列式子中,是分式的是( )A、
2. 下列式子中,是分式的是( )A、 B、
B、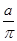 C、
C、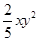 D、
D、 3. 4的平方根是( )A、 2 B、
3. 4的平方根是( )A、 2 B、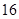 C、
C、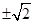 D、
4. 若二次根式 有意义,则实数x的取值范围是( )A、x≠3 B、x>3 C、x≥3 D、x<35. 如图,点 是 边 延长线上一点, , ,则 的度数是( )
D、
4. 若二次根式 有意义,则实数x的取值范围是( )A、x≠3 B、x>3 C、x≥3 D、x<35. 如图,点 是 边 延长线上一点, , ,则 的度数是( ) A、
A、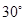 B、
B、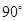 C、
C、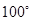 D、
D、 6. 科学家发现了一种新型病毒,其直径约为 ,数据 用科学记数法表示正确的是( )A、1.2×
6. 科学家发现了一种新型病毒,其直径约为 ,数据 用科学记数法表示正确的是( )A、1.2×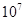 B、1.2×
B、1.2×  C、1.2×
D、1.2×
C、1.2×
D、1.2×  7. 长度分别为2,7,x的三条线段能组成一个三角形,
7. 长度分别为2,7,x的三条线段能组成一个三角形,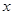 的值可以是( ) A、4 B、5 C、6 D、98. 不等式 的正整数解有( )A、4个 B、5个 C、6个 D、7个9. 如图,在△ABC中,∠BAC=90°,AB=AC,AE是经过A点的一条直线,且B,C在AE的两侧,BD⊥AE于D,CE⊥AE于E,CE=3,BD=9,则DE的长为( )
的值可以是( ) A、4 B、5 C、6 D、98. 不等式 的正整数解有( )A、4个 B、5个 C、6个 D、7个9. 如图,在△ABC中,∠BAC=90°,AB=AC,AE是经过A点的一条直线,且B,C在AE的两侧,BD⊥AE于D,CE⊥AE于E,CE=3,BD=9,则DE的长为( )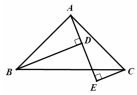 A、 B、
A、 B、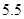 C、
D、7
10. 下列命题:①若 ,则 ;②两直线平行,内错角相等;③对顶角相等.它们的逆命题一定成立的有( )A、0个 B、1个 C、2个 D、3个11. 某口琴社团为练习口琴,第一次用 元买了若干把口琴,第二次在同一家商店用 元买同一款的口琴,这次商家每把口琴优惠 元,结果比第一次多买了 把.求第一次每把口琴的售价为多少元?若设第一次买的口琴为每把 元,列方程正确的是( )A、
C、
D、7
10. 下列命题:①若 ,则 ;②两直线平行,内错角相等;③对顶角相等.它们的逆命题一定成立的有( )A、0个 B、1个 C、2个 D、3个11. 某口琴社团为练习口琴,第一次用 元买了若干把口琴,第二次在同一家商店用 元买同一款的口琴,这次商家每把口琴优惠 元,结果比第一次多买了 把.求第一次每把口琴的售价为多少元?若设第一次买的口琴为每把 元,列方程正确的是( )A、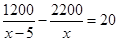 B、
B、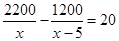 C、
C、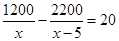 D、
D、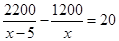 12. 已知非零实数 满足 ,则 的值是( )A、
12. 已知非零实数 满足 ,则 的值是( )A、 B、
B、 C、
C、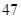 D、
D、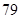
二、填空题
-
13. 计算:a5÷a2= .14. 计算: = .15. 若分式 的值为零,则x的值为 .
16. 如图,在 中, 的垂直平分线分别交 , 于点 , ,连接 ,如果 , ,则 的周长是 .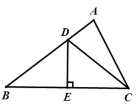 17. 已知三角形的三边长分别为 , , ,求其面积 的问题,古希腊数学家海伦在其著作《度量论》一书中给出了著名的海伦公式: ,其中 .若一个三角形的三边长分别为 , , ,则其面积是 .18. 如图,已知AB=AC,AD=BD=BC.在BC延长线上取点C1 , 连接DC1 , 使DC=CC1 , 在CC1延长线上取点C2 , 在DC1上取点E,使EC1=C1C2 , 同理FC2=C2C3 , 若继续如此下去直到Cn , 则∠Cn的度数为 . (结果用含 的代数式表示)
17. 已知三角形的三边长分别为 , , ,求其面积 的问题,古希腊数学家海伦在其著作《度量论》一书中给出了著名的海伦公式: ,其中 .若一个三角形的三边长分别为 , , ,则其面积是 .18. 如图,已知AB=AC,AD=BD=BC.在BC延长线上取点C1 , 连接DC1 , 使DC=CC1 , 在CC1延长线上取点C2 , 在DC1上取点E,使EC1=C1C2 , 同理FC2=C2C3 , 若继续如此下去直到Cn , 则∠Cn的度数为 . (结果用含 的代数式表示)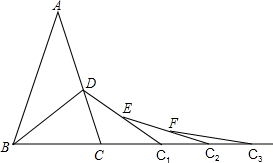
三、解答题
-
19. 计算:(1)、(2)、20. 解不等式组 ,并把解集在数轴上表示出来.
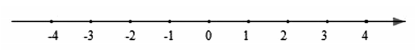 21. 解方程:22. 先化简,再求值: ,其中23. 尺规作图:保留作图痕迹,不写作法.
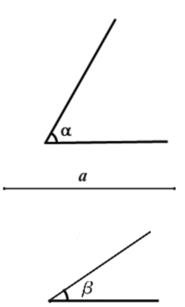
21. 解方程:22. 先化简,再求值: ,其中23. 尺规作图:保留作图痕迹,不写作法.已知:∠ ,∠ 和线段a
求作:△ABC,使∠B=∠ ,BC=a,∠C=∠ .
 24. 如图,点 , , , 在同一条直线上, , , .
24. 如图,点 , , , 在同一条直线上, , , . (1)、求证: ;(2)、当 , 时,求 的度数.25. 为庆祝广西壮族自治区成立60周年,某校团委组织开展了以“壮美广西”为主题的演讲比赛,并购买同一品牌的壮锦和画册作为奖励.已知购买一副壮锦比购买一副画册多用 元,若用 元购买壮锦和 元购买画册,则购买壮锦的数量是购买画册数量的 倍.(1)、求购买该品牌的每副画册和每副壮锦各需要多少元?(2)、经洽商,学校团委获得了购买一副该品牌的壮锦赠送一副该品牌的画册的优惠.如果本次活动需要的画册数量是壮锦数量的 倍少 副,且总费用不超过 元,那么学校团委最多可购买多少副壮锦?26. 如图①,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图②).
(1)、求证: ;(2)、当 , 时,求 的度数.25. 为庆祝广西壮族自治区成立60周年,某校团委组织开展了以“壮美广西”为主题的演讲比赛,并购买同一品牌的壮锦和画册作为奖励.已知购买一副壮锦比购买一副画册多用 元,若用 元购买壮锦和 元购买画册,则购买壮锦的数量是购买画册数量的 倍.(1)、求购买该品牌的每副画册和每副壮锦各需要多少元?(2)、经洽商,学校团委获得了购买一副该品牌的壮锦赠送一副该品牌的画册的优惠.如果本次活动需要的画册数量是壮锦数量的 倍少 副,且总费用不超过 元,那么学校团委最多可购买多少副壮锦?26. 如图①,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转α角(0°<α<180°),得到△AB′C′(如图②).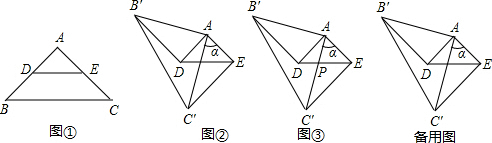 (1)、探究DB′与EC′的数量关系,并给予证明;(2)、当DB′∥AE时,求此时旋转角α的度数;(3)、如图③,在旋转过程中,设 AC′与DE所在直线交于点P,当△ADP成为等腰三角形时,求此时的旋转角α的度数.(直接写出结果)
(1)、探究DB′与EC′的数量关系,并给予证明;(2)、当DB′∥AE时,求此时旋转角α的度数;(3)、如图③,在旋转过程中,设 AC′与DE所在直线交于点P,当△ADP成为等腰三角形时,求此时的旋转角α的度数.(直接写出结果)