贵州省黔南州2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、选择题:
-
1. 下列各式① 、② 、③ 、④ 中,是分式的有( )A、①②④ B、②④ C、③④ D、②③④2. 我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化.窗框一部分如图2所示,它是一个轴对称图形,其对称轴有( )
 A、1条 B、2条 C、3条 D、4条3. 下列各题的计算,正确的是( )A、(a2)3=a5 B、(-3a2)3=-9a6 C、(-a)(-a)6=-a7 D、a3+a3=2a64. 下列说法正确的是( )A、三角形的一个外角大于任何一个内角 B、等腰三角形的任意两个角相等 C、三个角分别对应相等的两个三角形全等 D、三角形的三条高可能都在三角形内部5. 下列因式分解正确的是( )A、m2+n2=(m+n)(m—n) B、x2+2x-1=(x-1)2 C、a2-a=a(a-1) D、a2+2a+1=a(a+2)+16. 如图,BE=CF,AE⊥BC.DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需添加的一个条件是( )。
A、1条 B、2条 C、3条 D、4条3. 下列各题的计算,正确的是( )A、(a2)3=a5 B、(-3a2)3=-9a6 C、(-a)(-a)6=-a7 D、a3+a3=2a64. 下列说法正确的是( )A、三角形的一个外角大于任何一个内角 B、等腰三角形的任意两个角相等 C、三个角分别对应相等的两个三角形全等 D、三角形的三条高可能都在三角形内部5. 下列因式分解正确的是( )A、m2+n2=(m+n)(m—n) B、x2+2x-1=(x-1)2 C、a2-a=a(a-1) D、a2+2a+1=a(a+2)+16. 如图,BE=CF,AE⊥BC.DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需添加的一个条件是( )。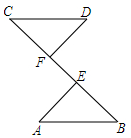 A、AE=DF B、∠A=∠D C、∠B=∠C D、AB=DC7. 若x2+bx+c=(x+5)(x-3),其中b,c为常数.则点P(b,c)关于x轴对称的点的坐标是( )
A、AE=DF B、∠A=∠D C、∠B=∠C D、AB=DC7. 若x2+bx+c=(x+5)(x-3),其中b,c为常数.则点P(b,c)关于x轴对称的点的坐标是( )
A、(-2,-15) B、(2,15) C、(-2,15) D、(2,-15)8. 如图,∠A=120°.且∠1=∠2=∠3和∠4=∠5=∠6,则∠BDC=( )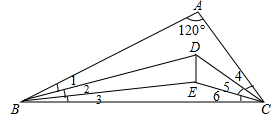 A、120° B、60° C、140° D、无法确定9. 施工队要铺设一段长2000米的管道,因在中考期间需要停工两天,实际每天施工需要比原计划多50米才能按时完成任务,求原计划每天施工多少米?设原计划每天施工x米,则根据题意所列方程正确的是( )A、
A、120° B、60° C、140° D、无法确定9. 施工队要铺设一段长2000米的管道,因在中考期间需要停工两天,实际每天施工需要比原计划多50米才能按时完成任务,求原计划每天施工多少米?设原计划每天施工x米,则根据题意所列方程正确的是( )A、 B、
B、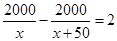 C、
C、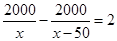 D、
D、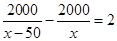 10. 如图,在等边△ABC中.AB=2。N为AB上一点,且AN=1,∠BAC的平分线交BC于点D.M是AD上的动点,连结BM、MN。则BM+MN的最小值是( ) 。
10. 如图,在等边△ABC中.AB=2。N为AB上一点,且AN=1,∠BAC的平分线交BC于点D.M是AD上的动点,连结BM、MN。则BM+MN的最小值是( ) 。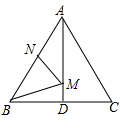 A、 B、2 C、1 D、3
A、 B、2 C、1 D、3二、填空
-
11. 已知三角形三边分别为l,x,5,则整数x= .12. 当m=时,分式 的值为0.13. 一个正多边形的每一个内角是108°,则这个正多边形的边数是14. 如图,在△ABC中,AB=AC,∠BAC=100°.AB的垂直平分线分别交AB、BC于点D、E,则∠BAE= 度.
15. 若有一种细菌的半径是5×10-4m,则用小数把它表示出来是 .
16. 若等腰三角形的周长是26cm,一边长为11cm,则腰长为17. 已知(x+y)2=36,(x-y)2=16,则xy= .18. 如图,已知△ABC的周长是21,0B、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是。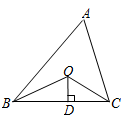
三、解答题:
-
19. 计算:(1)、-7m(-4m2p)2÷7m2(2)、(m-n)(m+n)+(m+n)2-2m220. 先化简,再求值: ,其中a=21. 如图,在平面直角坐标系中有一个△ABC,顶点A(-1,3),a(2,0),c(-3,-1).
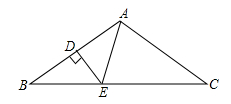
 (1)、画出△ABC关于y轴的对称图形△A1B1C1(不写画法),并写出点A1 , B1 , C1的坐标;(2)、求△ABC的面积.22. 已知:如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.
(1)、画出△ABC关于y轴的对称图形△A1B1C1(不写画法),并写出点A1 , B1 , C1的坐标;(2)、求△ABC的面积.22. 已知:如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.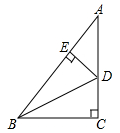 (1)、求证:BD平分∠ABC;(2)、若∠A=36°,求∠BDC的度数.23. 有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
(1)、求证:BD平分∠ABC;(2)、若∠A=36°,求∠BDC的度数.23. 有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案: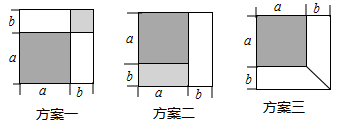
小明发现这三神方案都能验证公式:a2+2ab+b2=(a+b)2
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2
请你根据方案二、方案三,写出公式的验证过程.
方案二:
方案三:
24. 近几年,贵州高铁高速发展,现在贵州百姓外出旅行的路程与时间大大缩短,但也有不少旅客根据自己的喜好依然选择乘坐普通列车.已知从贵阳到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍.请完成以下问题:(1)、普通列车的行驶路程为千米;(2)、若高铁的平均速度是普通列车平均速度的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁列车的平均速度分别是多少?
25. 如图,平面直角坐标系中,点A、B分别在x、y轴上,点B的坐标为(0,1),∠BA0=30°.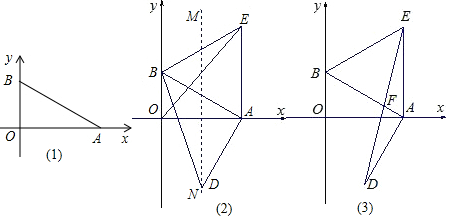 (1)、求AB的长度;(2)、分别以AB、AO为一边作等边△ABE、△AOD,求证:BD=EO:(3)、在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.
(1)、求AB的长度;(2)、分别以AB、AO为一边作等边△ABE、△AOD,求证:BD=EO:(3)、在(2)的条件下,连接DE交AB于F.求证:F为DE的中点.