浙江省嘉兴市2019届九年级上学期数学期末考试试卷
试卷更新日期：2019-03-26 类型：期末考试
一、选择题
-
1. 下列函数中，属于二次函数的是（ ）A、y=2x-1 B、y=x2+
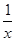C、y=x2(x+3)
D、y=x(x+1)
2. 如图，直线a∥b∥c，直线AC分别交a，b，c于点A，B，C；直线DF分别交a，b，c于点D，E，F.若 ；则 （ ）
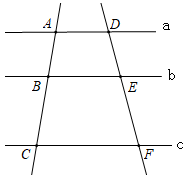A、
B、
C、
D、
3. 已知⊙O的半径为3cm，点A到圆心O的距离为4cm，那么点A到⊙O的位置关系是（ ）A、点A在⊙O内 B、点A在⊙O上 C、点A在⊙O外 D、不能确定4. 下列事件中，属于必然事件的是（ ）A、明年元旦会下雨 B、三角形三内角的和为180° C、抛一枚硬币正面向上 D、在一个没有红球的盒子里，摸到红球5. 下列二次函数的图象与x轴没有交点的是（ ）A、y=-3x2-4x B、y=x2-3x-4 C、y=x2-6x+9 D、y=2x2+4x+56. 已知线段AB的长为4，点P是线段AB的黄金分割点(AP>BP)，则PA的长为（ ）A、
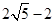B、
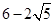C、
D、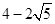
7. 若一个正多边形的一个内角为140°，则这个正多边形为（ ）A、正七边形 B、正八边形 C、正九边形 D、正十边形8. 如图，AB是⊙O的直径，点C是⊙O上的一点，过点C作CD⊥AB于点D，若4B=10，BC=6，则CD的长为（ ）
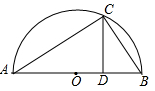A、1.2 B、2.4 C、4.8 D、59. 如图，有一块三角形余料ABC，BC=120mm，高线AD=80mm，要把它加工成一个矩形零件，使矩形的一边在BC上，点P，M分别在AB，AC上，若满足PM：PQ=3：2，则PM的长为（ ）
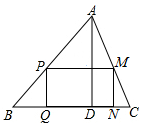A、60mm B、
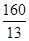mm
C、20mm
D、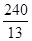
mm
10. 二次函数y=ax2+bx+c(a，b，c是常数，a<o)的图象经过A(-4，-4)，B(6，-4)，顶点为P，则下列说法中错误的是（ ）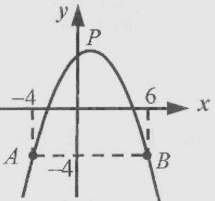
A、不等式ax2+bx+c>-4的解为-4<x<6 B、关于x的方程a(x+4)(x-6)-4=0的解与ax2+bx+c=0的解相同 C、若△PAB为等腰直角三角形，则a=-
D、当t≤x≤t+2时，二次函数y=ax2+bx+c的最大值为at2+bt+c，则t≥0
二、填空题
-
11. 若 ，则 = ．12. 在一个不透明的袋中装有只有颜色不同的10个球，其中6个红色，4个白色，从袋中任意摸出一个球是红球的概率是 ．13. 将抛物线y=x2-2向左平移1个单位后所得抛物线的表达式为 ．14. 如图，等腰△ABC的顶角∠BAC=50°，以AB为直径的半圆分别交BC，AC于点D，E．则的度数是 度．
15. 如图，有一块三角板AB0，∠B=30°，直角顶点D与量角器的中心重合，AB与量角器交于点A，C．若量角器的半径为5cm，则线段BC的长为 ．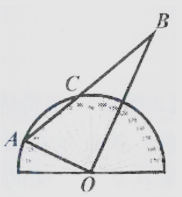
16. 如图，在四边形ABCD中，AD∥BC∥EF，EF分别与AB，AC，CD相交于点E，M，F．若EM：BC=2：5，则FC：CD的值是 ．
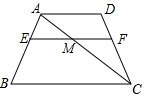17. 如图，矩形ABCD中，AB=2，BC=4，剪去一个矩形ABEF后，余下的矩形EFDC∽矩形BCDA，则EC的长为．
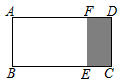18. 如图，在Rt△ABC中，∠ABC=90°，∠ACB=30°，AC=6，现将Rt△ABC绕点A顺时针旋转30°得到△AB'C’，则图中阴影部分面积为 ．
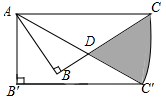19. 如图，P为AABC的重心，连结AP并延长交BC于点D，过点P作EF∥BC分别交AB，AC于点E，F．若△ABC的面积为18，则△AEF的面积为 ．
20. 如图，⊙O的半径为1，弦AB=，BC=-，AB，BC在圆心O的两侧，AC上有一动点D，AE⊥BD于点E．当点D从点C运动到点A时，则点E所经过的路径长为 ．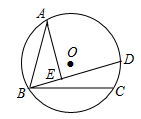
三、解答题
-
21. 已知抛物线y=-x2+4x+5，(1)、求抛物线与y轴交点的坐标；(2)、求抛物线的对称轴．22. 如图，已知正△ABC，
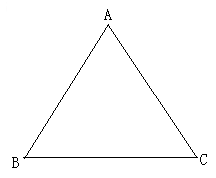(1)、请用直尺与圆规作正△ABC的外接圆 ，并保留作图痕迹；
(2)、若点P是正△ABC的外接圆上的一点(不与点B，C重合)，求∠BPC的度数．23. 如图，有一个可自由转动的转盘被分成3等份，每份内标有数字分别是1，2，3．用这个转盘自由转动两次，每次停止转动后，指针落在所示区域的数字(如果指针恰好停在等分线上，那么重转一次，直到指针落在某一区域的数字为止)；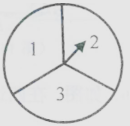
(1)、请用树状图或列表法表示两次转动后指针落在所示区域的数字所有可能的结果；(2)、求指针两次落在区域的数字相加的和大于4的概率是多少?24. 如图，在△ABC中，AB=AC，∠BAC=90°，点D、E分别在边BC，AC上(不与端点重合)，连结AD，DE，若∠ADE=45°．
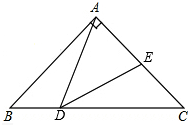(1)、求证：△ABD∽△DCE；(2)、若AB=4 ，BD=1，求AE的长．25. 如图，已知抛物线y=ax2+bx+3过点A(-1，0)，B(3，0)，交y轴于点C，点M是该抛物线上第一象限内的一个动点，ME⊥x轴于点E，交线段BC于点D，MN∥x轴，交y轴于点N．
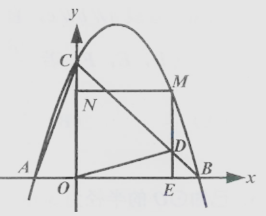(1)、求抛物线y=ax2+bx+3的表达式；(2)、若四边形MNOE是正方形，求该正方形的边长；(3)、连结OD，AC，抛物线上是否存在点M，使得以点C，O，D为顶点的三角形与△ABC相似，若存在，请求出点M的坐标，若不存在请说明理由．26. 嘉兴某公司抓住“一带一路”的机遇不断创新发展，生产销售某产品．该产品销售量y(万件)与售价x(元／件)之间存在图1(一条线段)所示的变化趋势，总成本P(万元)与销售量y(万件)之间存在图2所示的变化趋势，当6≤y≤10时可看成一条线段，当10≤y≤18时可看成抛物线P=- y2+8y+m．
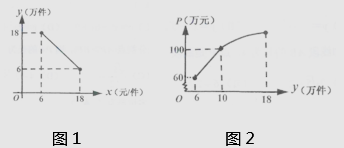(1)、写出y与x之间的函数关系式；(2)、若销售量不超过10万件时，利润为45万元，求此时的售价为多少元／件?(3)、当售价为多少元时，利润最大，最大值是多少万元?(利润=销售总额-总成本)