陕西省西安未央区2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、选择题
-
1. 下列函数中,y是x反比例函数的是( )A、y= B、
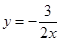 C、
C、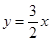 D、
D、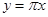 2. 矩形木框在阳光照射下,在地面上的影子不可能是( )A、
2. 矩形木框在阳光照射下,在地面上的影子不可能是( )A、 B、
B、 C、
C、 D、
D、 3. 如下图,在△ABC中,点D在边AB上,则下列条件中不能判断△ABC∽△ACD的是( )
3. 如下图,在△ABC中,点D在边AB上,则下列条件中不能判断△ABC∽△ACD的是( )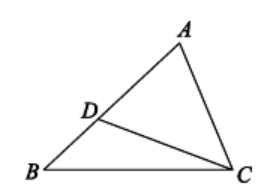 A、∠ABC=∠ACD B、∠ADC=∠ACB C、
A、∠ABC=∠ACD B、∠ADC=∠ACB C、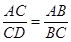 D、AC2=AD·AB
4. 如下图,四边形ABCD和A’B’C’D’是以点O为位似中心的位似图形,若OA’:OA=3:5,四边形A’B’C’D’的面积为9 cm2 , 则四边形ABCD的面积为( )
D、AC2=AD·AB
4. 如下图,四边形ABCD和A’B’C’D’是以点O为位似中心的位似图形,若OA’:OA=3:5,四边形A’B’C’D’的面积为9 cm2 , 则四边形ABCD的面积为( )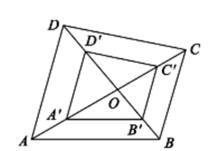 A、15cm2 B、25cm2 C、18cm2 D、27cm25. 把同一副扑克牌巾的红桃2、红桃3、红桃4三张牌背面朝上放在桌子上,从中随机抽取两张,牌面的数字之和为奇数的概率为( )A、
A、15cm2 B、25cm2 C、18cm2 D、27cm25. 把同一副扑克牌巾的红桃2、红桃3、红桃4三张牌背面朝上放在桌子上,从中随机抽取两张,牌面的数字之和为奇数的概率为( )A、 B、
C、
D、
6. 如图,点A(3,t)在第一象限,0A与x轴所夹的锐角为a,tana= ,则t=( )
B、
C、
D、
6. 如图,点A(3,t)在第一象限,0A与x轴所夹的锐角为a,tana= ,则t=( )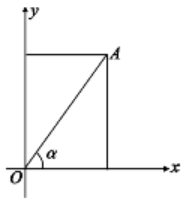 A、0.5 B、1.5 C、4.5 D、27. 如图,在同一平面直角坐标系巾,反比例函数y= 与一次函数y=kx+3(k为常数,且k>0)的图象可能是( )A、
A、0.5 B、1.5 C、4.5 D、27. 如图,在同一平面直角坐标系巾,反比例函数y= 与一次函数y=kx+3(k为常数,且k>0)的图象可能是( )A、 B、
B、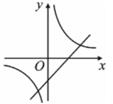 C、
C、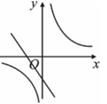 D、
D、 8. 如图,在 ABCD巾,点M在BC边上,且BM=BC,AM与BD相交于点N,那么s△BMN:s ABCD为( )
8. 如图,在 ABCD巾,点M在BC边上,且BM=BC,AM与BD相交于点N,那么s△BMN:s ABCD为( )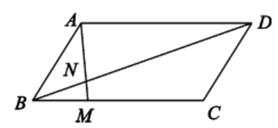 A、1:3 B、1:9 C、1:12 D、1:249. 兰兰和笑笑分别解一道关于X的一元二次方程,兰兰因把一次项系数看错,解得方程两根为-2和6,笑笑因把常数项看错,解得方程两根为3和4,则原方程是( )A、x2+7x-12=0 B、x2-7x-12=0 C、x2+7x+12=0 D、x2-7x+12=010. 已知二次函数Y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ①abc>0 ②b<a+c③4a+2b+c>0 ④2c<3b ⑤a+b>m(am+b)(m≠1的实数),其中正确的结论有( )
A、1:3 B、1:9 C、1:12 D、1:249. 兰兰和笑笑分别解一道关于X的一元二次方程,兰兰因把一次项系数看错,解得方程两根为-2和6,笑笑因把常数项看错,解得方程两根为3和4,则原方程是( )A、x2+7x-12=0 B、x2-7x-12=0 C、x2+7x+12=0 D、x2-7x+12=010. 已知二次函数Y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: ①abc>0 ②b<a+c③4a+2b+c>0 ④2c<3b ⑤a+b>m(am+b)(m≠1的实数),其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题。
-
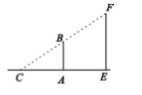
11. 抛物线y=-x2+15有最值,顶点坐标是 .12. 用配方法将方程x2-4x+1=0化成(x+m)2=n的形式(m、n为常数),则 =13. 存矩形ABCD中,AB=6,AD=5,点P是BC上的一个动点,连接AP、DP,则AP+DP的最小值为 .14. 如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=4m,在旋转过程中,影长的最大值为5m,最小值为4m,且影长最大时,木杆与光线乖直,则路灯EF的高度为m.
三、解答题
-
15. 计算:(1)、( -2)0+|2- |+2cos30°;
(2)、6tan230°- sin60°-2cos45°.16. 用公式法解方程:x2-3x-4=0.17. 如图,在等腰△ABC巾,AD是顶角∠BAC的角平分线,BE是腰AC边上的高,垂足为点E,求证:△ACD∽△BCE.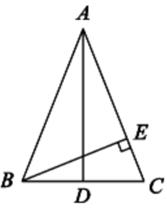 18. 如图,是由一些棱长为单位1的相同的小正方体组合成的简单几何体.
18. 如图,是由一些棱长为单位1的相同的小正方体组合成的简单几何体.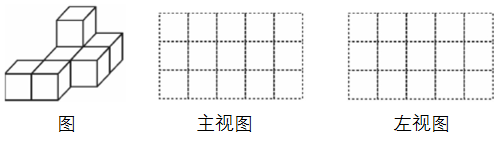 (1)、图中有个小正方体;(2)、请在图右侧方格中分别画出几何体的主视图和左视图19. 如图所示,某体育场内一看台AB=10 米,高BC=5 米,A,B两点正前方有垂直丁地面的旗杆DE,存A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角).
(1)、图中有个小正方体;(2)、请在图右侧方格中分别画出几何体的主视图和左视图19. 如图所示,某体育场内一看台AB=10 米,高BC=5 米,A,B两点正前方有垂直丁地面的旗杆DE,存A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角). (1)、求旗杆DE的高度;(2)、已知旗杆上有一面旗存离地面1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?20. 如图,已知在正方形ABCD巾,点E足BC边上一点,F为AB延长线上一点,且BE=BF,连接AE、EF、CF.
(1)、求旗杆DE的高度;(2)、已知旗杆上有一面旗存离地面1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?20. 如图,已知在正方形ABCD巾,点E足BC边上一点,F为AB延长线上一点,且BE=BF,连接AE、EF、CF. (1)、若∠BAE=18°,求∠EFC的度数;(2)、求证:AE⊥CF.21. 如图,一块材料的形状是锐角三角形ABC,边BC长13cm,BC边上的高AD为6 cm,把它加上成正方形零件,使正方形的一边在BC上,其余两个顶点分别存AB、AC上.
(1)、若∠BAE=18°,求∠EFC的度数;(2)、求证:AE⊥CF.21. 如图,一块材料的形状是锐角三角形ABC,边BC长13cm,BC边上的高AD为6 cm,把它加上成正方形零件,使正方形的一边在BC上,其余两个顶点分别存AB、AC上.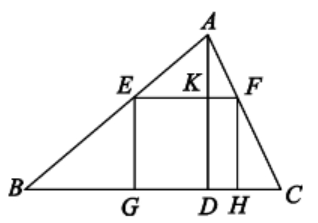 (1)、求证:△AEF∽△ABC;(2)、求这个正方形零件的边长.22. 盒中有若干枚黑球和白球,这些球除颜色外尤其他差别,现让学生进行摸球试验:每次摸m一个球,记下颜色后放回摇匀.重复进行这样的试验得到以下数据:
(1)、求证:△AEF∽△ABC;(2)、求这个正方形零件的边长.22. 盒中有若干枚黑球和白球,这些球除颜色外尤其他差别,现让学生进行摸球试验:每次摸m一个球,记下颜色后放回摇匀.重复进行这样的试验得到以下数据:摸球的次数n
100
200
300
500
800
1000
摸到白球的次数m
38
79
121
196
322
398
摸到白球的频率 (精确到0.001)
0.380
0.395
0.403
0.392
0.403
0.398
(1)、根据表中数据估计,从盒巾摸出一个球是白球的概率是;(精确到0.01)(2)、若盒中黑球与白球共有5枚,某同学连续不放回地摸出两个球,用树状图或表格计算这两个球颜色不同的概率.23. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A(m,4)、B(2,-6)两点,过A作AC⊥x轴交于点C,连接OA.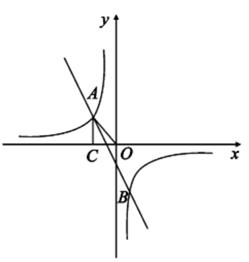 (1)、分别求出一次函数与反比例函数的表达式;(2)、若直线AB上有一点M,连接MC,且满足S△AMC=3S△AOC , 求点M的坐标.24. 如图,抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0),与y轴交于点C,连接BC.
(1)、分别求出一次函数与反比例函数的表达式;(2)、若直线AB上有一点M,连接MC,且满足S△AMC=3S△AOC , 求点M的坐标.24. 如图,抛物线y=ax2+bx+3与x轴交于点A(-1,0),B(3,0),与y轴交于点C,连接BC.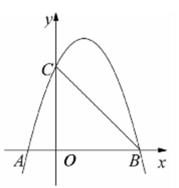 (1)、求抛物线的表达式;(2)、求抛物线的顶点式并写出对称轴和顶点坐标;(3)、抛物线上是否存在点M,使得△MBC的面积与△OBC的面积相等,若存在,请写出点M的坐标;若小存在,请说明理由.25. 如图,在矩形ABCD中,AB=10m,BC=24m,动点P以2 m/s的速度从A点出发,沿AC向C点移动,同时动点p以1m/s的速度从C点出发,沿CB向B点移动,设P、Q两点移动的时间为t秒.(0<t<13)
(1)、求抛物线的表达式;(2)、求抛物线的顶点式并写出对称轴和顶点坐标;(3)、抛物线上是否存在点M,使得△MBC的面积与△OBC的面积相等,若存在,请写出点M的坐标;若小存在,请说明理由.25. 如图,在矩形ABCD中,AB=10m,BC=24m,动点P以2 m/s的速度从A点出发,沿AC向C点移动,同时动点p以1m/s的速度从C点出发,沿CB向B点移动,设P、Q两点移动的时间为t秒.(0<t<13)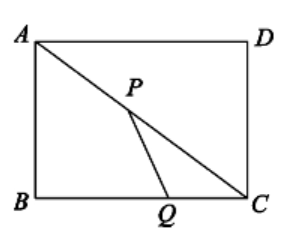 (1)、t为多少时,以P、Q、C为顶点的三角形与△ABC相似?(2)、探究:在P、Q两点移动过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
(1)、t为多少时,以P、Q、C为顶点的三角形与△ABC相似?(2)、探究:在P、Q两点移动过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时t的值;若不能,请说明理由.