浙江省湖州市浙江省湖州市德清县2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期：2019-03-26 类型：期末考试
一、选择题
-
1. 抛物线y=2(x+3)2+5的顶点坐标是（ ）．A、(3，5) B、(-3，-5) C、(3，-5) D、(-3，5)2. 在“绿水青山就是金山银山”这句话中任选一个汉字，这个字是“绿”的概率为（ ）．A、
B、
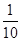C、
D、
3. 一架5米长的梯子斜靠在墙上，测得它与地面的夹角为40°，则梯子底端到墙角的距离为（ ）A、5cos40°米 B、5sin40°米 C、
米
D、
米
4. 如图，在⊙O中，OC垂直于弦AB于点C，AB=4，OC=1，则OB的长是（ ）．
A、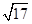
B、
C、
D、
5. 二次函数y=ax2+bx+c(a≠0)的图象如图所示，下列结论正确的是（ ）．
A、a>0 B、abc>O C、2a+b<0 D、ax2+bx+c=o有两个不相等的实数根6. 如图，⊙O是△ABC的外接圆，BC=2，∠BAC=30°，则劣弧BC的长等于（ ）．
A、
B、
C、
D、
7. 如图，在△ABC中，点D，E分别是边AC，AB的中点，BD与CE交于点D，连接DE．下列结论：① ；② ；③ ；④ 其中正确的个数有（ ）．
A、1个 B、2个 C、3个 D、4个8. 如图，已知直线a∥b∥c，直线m分别交直线a、b、C于点A，B，C，直线n分别交直线a、b、c于点D，E，F．若AB=3，AD=BC=5，则 的值应该（ ）．
A、等于
B、小于
C、大于
D、不能确定
9. 如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点△ABC的外部，则下列叙述正确的是（ ）．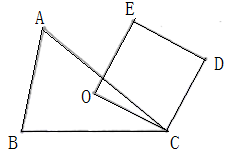
A、D是△AEB的外心，O是△AED的外心 B、O不是△AEB的外心，O不是△AED的外心 C、D不是△AEB的外心，O是△AED的外心 D、O是△AEB的外心，O不是△AED的外心10. 如图，以G(0，2)为圆心，半径为4的圆与x轴交于A，B两点，与y轴交于C，D两点，点E为⊙G上一动点，且点E在第一象限，CF⊥AE于点F，当点E在⊙G的圆周上运动的过程中，线段BF的长度的最小值为（ ）．
A、3 B、2 -2
C、6-2
D、4-
二、填空题
-
11. 如果b=4是a与c的比例中项，且a=3，那么c= ．12. 若质量抽检时任抽一件西服成品为合格品的概率为0.9，则200件西服中大约有合格品．13. 将抛物线 先向左平移 个单位，再向下平移 个单位，所得抛物线的解析式为 ．14. 如图，在网格(每个小正方形的边长均为1)中选取7个格点(格线的交点称为格点)，如果以A为圆心，r为半径画圆，选取的格点中除点A外恰好有3个在圆内，则r的取值范围为 ．
15. 如图，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处．若△AEM与△ECM相似，则AB和BC的数量关系为 ．
16. 已知x轴上有点A(1，0)，点B在y轴上，点C(m，0)为x轴上一动点且m<-1，连接接AB，BC，tan∠ABO= ，以线段BC为直径作⊙M交线段AB于点D，过点B作直线l∥AC，过A，B，C三点的抛物线为y=ax2+bx+c，直线l与抛物线和⊙M的另一个交点分别是E，F，当EF=BD时，则m的值为 ．
三、解答题
-
17. 计算：4sin260°+tan45°-8cos230°．18. 为了做好防控H1N1甲型流感工作，我县卫生局准备从甲、乙、丙三位医生和A、B两名护士中选取一位医生和一名护士指导某乡镇预防H1N1甲型流感工作·(1)、若随机选一位医生和一名护士，用树状图(或列表法)表示所有可能出现的结果；(2)、求恰好选中医生甲和护士A的概率．19. 如图，⊙D是△ABC的外接圆，AB=AC，P是⊙O上一点．请你只用无刻度的直尺，分别画出图①和图②中∠P的平分线，保留画图痕迹．
20. 如图，点C，D在线段AB上，CD2=AC·DB，且△PCD是等边三角形．
(1)、证明：△ACP∽△PDB；(2)、求∠APB的度数．21. 在平面直角坐标系xOy中，二次函数y=mx2-(2m+1)x+m-4的图象与x轴有两个公共点，m取满足条件的最小的整数·(1)、求此二次函数的解析式；(2)、当n≤x≤1时，函数值y的取值范围是一5≤y≤1-n，求n的值·22. 如图，某中学准备围建一个矩形苗圃，其中一边靠墙，另外三边用长为30米的篱笆围成，若墙长为18米，设这个苗圃垂直于墙的一边长为x米。
(1)、若苗圃园的面积为100平方米，求x的值；(2)、若平行于墙的一边长不小于8米，这个苗圃园的面积有最大值和最小值吗?如果有，求出最大值和最小值；如果没有，请说明理由·23. 如图，AB是⊙D的直径，D、E为⊙O上位于AB异侧的两点，连接BD并延长至点C，使得CD=BD，连接AC交⊙O于点F，连接AE、DE、DF
(1)、求证：∠E=∠C；(2)、若∠E=50°，求∠BDF的度数；(3)、设DE交AB于点G，若DF=6，cosB= ，E是AB的中点，求EG·ED的值．24. 如图，已知抛物线y=ax2+bx+3(a≠0)与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心M(1，m)恰好在此抛物线的对称轴上，⊙M的半径为 ．设⊙M与y轴交于点D，抛物线的顶点为E·
(1)、求m的值及抛物线的解析式；(2)、∠DBC= ，∠CBE= ，求sin( - )的值；(3)、探究：在坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似?若存在，请直接写出点P的坐标；若不存在，请说明理由．