浙江省温州市2019届九年级下学期数学中考模拟试卷
试卷更新日期:2019-03-26 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分。每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
1. -2的相反数是( )A、2 B、-
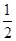 C、-2
D、-
C、-2
D、- 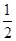 2. 截至目前中国森林面积达到175 000 000公顷,森林覆盖率为18.21%,人工林面积居世界首位,其中数字175 000 000用科学记数法表示为( )A、179×106 B、17.5×107 C、1.75×108 D、0.175×1093. 一个几何体的三视图如图所示,则这个几何体是( )
2. 截至目前中国森林面积达到175 000 000公顷,森林覆盖率为18.21%,人工林面积居世界首位,其中数字175 000 000用科学记数法表示为( )A、179×106 B、17.5×107 C、1.75×108 D、0.175×1093. 一个几何体的三视图如图所示,则这个几何体是( )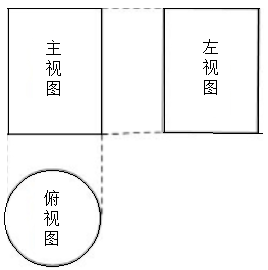 A、圆柱 B、圆锥 C、长方体 D、正方体4. 在一个不透明的袋子内装有2个红球、3个红球和4黑球,它们除了颜色外其余均相同,从中任意摸出一个红球的概率是 ( )A、 B、 C、
A、圆柱 B、圆锥 C、长方体 D、正方体4. 在一个不透明的袋子内装有2个红球、3个红球和4黑球,它们除了颜色外其余均相同,从中任意摸出一个红球的概率是 ( )A、 B、 C、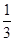 D、
5. 甲,乙,内,丁四名同学在学校演讲选拔赛的成绩平均数 方差s2如下表所示:
D、
5. 甲,乙,内,丁四名同学在学校演讲选拔赛的成绩平均数 方差s2如下表所示:甲
乙
丙
丁
平均数
8.0
8.0
8.5
8.5
方差s2
3.5
15.5
3.5
16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁6. 如图,是一个三角板,则下列选项中可能是由该图经过一次轴对称变换后得到的是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,矩形ABCD是一道门的门框,将一条长为1米的木棒的一端放在门框AB上的点E处,将木棒靠在左边门框AD上时,另一端落在点G处,保持一端在点E不动,将木棒靠在右边门框BC时,另一端落在点F处.测得∠AGE=30°,∠EFB=45°,则与门框的宽度AB最接近的长度为( )(参考: ≈1.414, ≈1.732)
7. 如图,矩形ABCD是一道门的门框,将一条长为1米的木棒的一端放在门框AB上的点E处,将木棒靠在左边门框AD上时,另一端落在点G处,保持一端在点E不动,将木棒靠在右边门框BC时,另一端落在点F处.测得∠AGE=30°,∠EFB=45°,则与门框的宽度AB最接近的长度为( )(参考: ≈1.414, ≈1.732) A、1米 B、1.2米 C、1.5米 D、1.6米8. 某果糖店的甲,乙两种果糖的销售单价分别为每公斤a,b元,先将m公斤甲种果糖和n公斤乙种果糖混合成什锦糖,店长为了保持利润不变,则该什锦糖每公斤应定价为( )
A、1米 B、1.2米 C、1.5米 D、1.6米8. 某果糖店的甲,乙两种果糖的销售单价分别为每公斤a,b元,先将m公斤甲种果糖和n公斤乙种果糖混合成什锦糖,店长为了保持利润不变,则该什锦糖每公斤应定价为( )
A、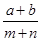 B、
B、 C、a+b
D、
C、a+b
D、 9. 在直角坐标系中,直线y=x+2和抛物线y=x2-x+1的若干组函数值如下表所示:
9. 在直角坐标系中,直线y=x+2和抛物线y=x2-x+1的若干组函数值如下表所示:x
…
1
1.5
2
2.5
3
…
y=x+2
…
3
3.5
4
4.5
6
…
y=x2-x+1
…
1
1.75
3
4.75
13
…
根据表格,这两个图象一个交点的横坐标范围是( )
A、1<x<1.5 B、1.5<Xx2 C、2<x<2.5 D、2.5<x<310. 如图,存Rt△ABC中,∠ACB=90°,以AB为边向下作正方形ADEB,连结CD,CE.分别记△ACD,△BCE的面积为S1 , S2 , 用S1 , S2的代数式表示边AB的长为( )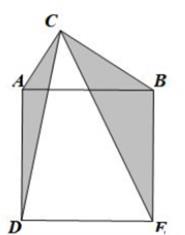 A、
A、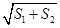 B、
B、 C、
C、 D、
D、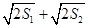
二、填空题(共有6小题,每小题5分,共30分)
-
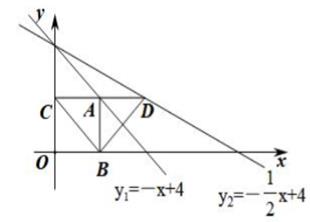
11. 因式分解:4-9x2= .12. 要使根式 有意义,则字母x的取值范围是 .13. 一个正n多边形的内角和是它外角和的2倍,则n= .14. 如图,点A在直线y1=-x+4上,且位于第一象限.AB⊥x轴于点B,AC⊥y轴于点C,延长CA交直线y2=- x+4于点D,连结BC,BD.若 ,则△BCD 的周长 .
 15. 小东同学将“L”型尺子和量角器按如图所示摆放,其中“L”型尺子的一边AB与量角器的零度线在同一直线上,另一边BC与量角器相切于点B.且AB=OB.P为BC边上一点,射线PM经过点A,射线PN与量角器切于点D.若点D在量角器上的读数为50°,则∠MPN的度数为 .
15. 小东同学将“L”型尺子和量角器按如图所示摆放,其中“L”型尺子的一边AB与量角器的零度线在同一直线上,另一边BC与量角器相切于点B.且AB=OB.P为BC边上一点,射线PM经过点A,射线PN与量角器切于点D.若点D在量角器上的读数为50°,则∠MPN的度数为 . 16. 如图,A,B是反比例函数 (k>0)卜两点,纵坐标分别为3,1,连结AO并延长交双曲线于另一点C,连结BC.若AC=BC,则k的值为 .
16. 如图,A,B是反比例函数 (k>0)卜两点,纵坐标分别为3,1,连结AO并延长交双曲线于另一点C,连结BC.若AC=BC,则k的值为 .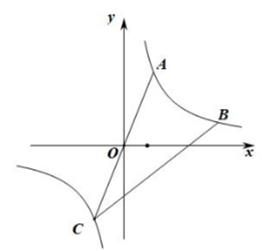
三、解答题
-
17. 计算题(1)、计算:(2)、化简:a(a-2)-(2a-1)(2a+1)+2a.18. 如图,在 ABCD中,点E,F和对角线AC上,连结BE,DF,若BE∥DF.
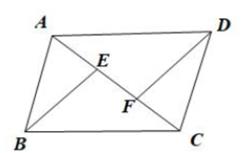 (1)、求证:△ADF≌△CBE.(2)、若AF=8,AC=13,求EF的长.19. 如图,由边长为1个单位的小正方形组成了10×10的网格,每个小正方形的顶点称为格点.如图,点A,B均为格点.
(1)、求证:△ADF≌△CBE.(2)、若AF=8,AC=13,求EF的长.19. 如图,由边长为1个单位的小正方形组成了10×10的网格,每个小正方形的顶点称为格点.如图,点A,B均为格点. (1)、在图①中确定格点C,D,使得以A,B,C,D为顶点的四边形为矩形,且矩形的邻边之比为1:2,作出一个这样的矩形.
(1)、在图①中确定格点C,D,使得以A,B,C,D为顶点的四边形为矩形,且矩形的邻边之比为1:2,作出一个这样的矩形.
(2)、在图②中确定格点C,D,使得以A,B,C,D为顶点的四边形为平行四边形,且其中一个内角的正切值为2,作出一个这样的平行四边形.
20. 为了提倡节约用水,某市自来水制定了二级收费标准,具体收费如下表:每月用水量a吨
第一级用水量a≤20
第二级用水量20<a≤30
第三级用水量a>30
水费(元/吨)
2.4
3.5
4.5
(注:第二,三级水费均为超出部分的水费).
该市某用户在4月1日到6日这6天的用水量如下图所示:
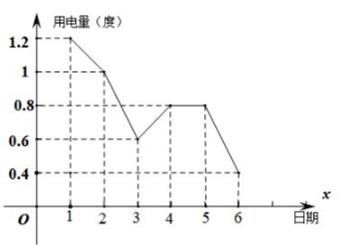 (1)、求该用户在这6天的用水量的众数和中位数.(2)、该用户4月份平均每天用水量与这6天的平均每天用水量相同.由于天气变热,4,5,6月份的用水量逐月增加.若5,6两个月合计用水60吨,共缴水费170元,求该用户在5,6月分别用了多少吨水?
(1)、求该用户在这6天的用水量的众数和中位数.(2)、该用户4月份平均每天用水量与这6天的平均每天用水量相同.由于天气变热,4,5,6月份的用水量逐月增加.若5,6两个月合计用水60吨,共缴水费170元,求该用户在5,6月分别用了多少吨水?
21. 如图,△ABC是⊙O的内接三角形,且AB为⊙O的直径.点D在 ⊙O 上且BC=BD,连结AD,过点D作DE⊥BC于点E,交AB于点F,连结CF.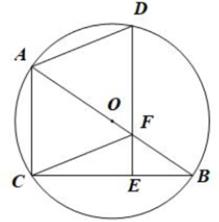 (1)、求证:四边形ACFD是菱形.(2)、若DE=12,BC=13,求线段AC的长.
(1)、求证:四边形ACFD是菱形.(2)、若DE=12,BC=13,求线段AC的长.
22. 如图,在坐标系中, 抛物线y=-x2+x+4交y轴于点A ,点P(4,p)存第一象限内,且在抛物线的下方.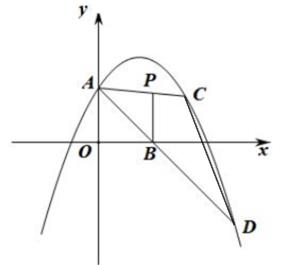 (1)、求P的取值范围.(2)、过点P作PB⊥x轴于点B,延长AP,AB分别交抛物线于点C,D,连结CD,当S△ACD的值最大时,求P的值.23. 活动课上,学习小组对小明同学正常走路的步长、步数之间的关系进行了测量,得到如下关系:n=160p,其中n表示每分钟走的步数,p(米)表示两个相连脚步脚跟间(或脚尖间)的距离.
(1)、求P的取值范围.(2)、过点P作PB⊥x轴于点B,延长AP,AB分别交抛物线于点C,D,连结CD,当S△ACD的值最大时,求P的值.23. 活动课上,学习小组对小明同学正常走路的步长、步数之间的关系进行了测量,得到如下关系:n=160p,其中n表示每分钟走的步数,p(米)表示两个相连脚步脚跟间(或脚尖间)的距离. (1)、当小明以每分钟80的步数走完100米需要几步?(2)、小明每分钟走的路程为S(米).请写出S关于p的函数关系式: .
(1)、当小明以每分钟80的步数走完100米需要几步?(2)、小明每分钟走的路程为S(米).请写出S关于p的函数关系式: .
(3)、小明每分钟走的路程为S(米).小东正常走路的步长、步数之间的关系为n1=kp1(k为常量),小明和小东匀速走完100米均用1.6分钟,小东比小明少走了20步,若小东走完100米恰好用了整数步,求k的值.(注:如图所示,脚尖紧靠起点线内侧至脚尖跟刚好触碰到终点线为走完100米)
24. 在△OBD中,OB⊥OD,∠OBD=30°,点A,C分别在BO,DO的延长线上,且AC=BD,E为AC的中点,连结DE,交AO于点F.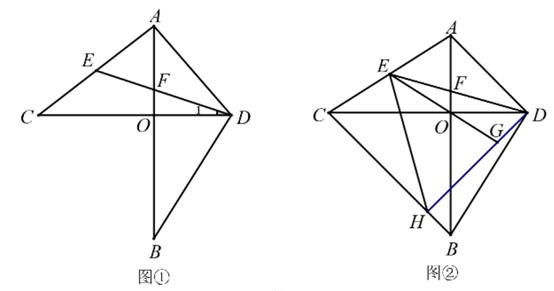 (1)、如图①,判断∠C和∠1数量关系,并说明理由.(2)、如图①,当△AFE是等腰三角形时,求∠1的度数.
(1)、如图①,判断∠C和∠1数量关系,并说明理由.(2)、如图①,当△AFE是等腰三角形时,求∠1的度数.
(3)、如图②,当OA=OD时,过点D作DH⊥BC于点H.①求证:DE=DH.
②连结EH,延长 EO交DH 于点G,求S△HEG:S△DFG的值.