浙江省湖州市浙江省湖州市德清县2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-03-26 类型：期末考试
一、选择题 下面每小题给出的四个选项中，只有一个是正确的，请选出各题中一个最符合题意的选项，并在答题卷上将相应题次中对应字母的方框涂黑，不选、多选、错选均不给分．
-
1. 下列各点中，在第四象限的点是（ ）．A、(2，3) B、(-2，-3) C、(2，-3) D、(-2，3)2. 人字梯中间一般会设计一”拉杆”，这样做的道理是（ ）．
A、两点之间，线段最短 B、垂线段最短 C、两直线平行，内错角相等 D、三角形具有稳定性3. 现有2cm，5cm长的两根木棒，再从下列长度的四根木棒中选取一根。可以围成一个三角形的是（ ）．A、2cm B、3cm C、5cm D、7cm4. 下列命题中，是真命题的是（ ）．A、两个锐角之和为钝角 B、相等的两个角是对顶角 C、同位角相等 D、钝角大于它的补角5. 如果等腰三角形有一个内角为70°，则其底角的度数是（ ）．A、55° B、70° C、55°或70° D、不确定6. 小明在研究矩形的时候，利用直尺和圆规作出了如图的图形，依据尺规作图的痕迹，可知∠a的度数为（ ）．
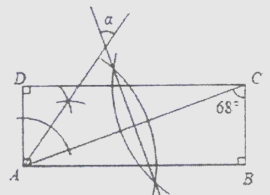A、56° B、68° C、28° D、34°7. 一次函数y=(m-2)x+(m-1)的图象如图所示，则m的取值范围是（ ）．
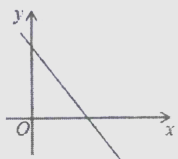A、m<2 B、1<m<2 C、m<1 D、m>28. 如图，已知∠AOE=∠BOE=15°，EF∥OB，EC⊥OB于点C，EG⊥OA于点G，若EC= ，则OF长度是（ ）．
A、2
B、
C、3
D、2
9. 关于x的不等式组 恰好只有两个整数解，则a的取值范围为（ ）．
A、5≤a<6 B、5<a≤6 C、4≤a<6 D、4<a≤610. 八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（ ）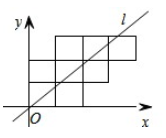
A、
B、
C、
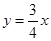D、y=x
二、填空题
-
11. 已知x>y，则2x2y(填“>””<”或“=”)．12. 命题“两直线平行，同旁内角互补”的逆命题是 ．13. 如图，已知∠ABC=∠DCB，要用SAS判断△ABC≌△DCB，需增加一个条件： ．
14. 如图，在平面直角坐标系中，点A、B的坐标分别为(0，4)和(1，3)，△OAB沿x轴向右平移后得到△D’A’B’，且点A的对应点A’在直线 上，则点B’坐标为 ．
15. 已知在平面直角坐标系中，等腰直角三角形ABC的斜边AB的端点A、B分别在y轴和x轴上，且点A(0，4)，B(3，0)，直角顶点C在第一象限，则点C的坐标为 ．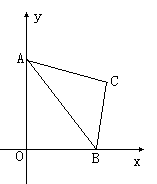
16. 如图，Rt△ABC纸片中，∠C=90°，AC=3，BC=4，点D在边BC上，以AD为折痕将△ABD折叠得到△AB’D，AB'与边BC交于点E．若 △DEB’ 为直角三角形，则BD的长是 ．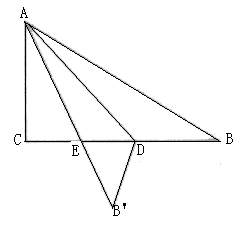
三、解答题
-
17. 解不等式组18. 在平面直角坐标系xOy中，△ABC的位置如图所示．
(1)、分别写出△ABC各个顶点的坐标：A( ， )；B( ， )：C( ， )：
(2)、顶点A关于x轴对称的点A’的坐标( ， )；顶点C关于原点对称的点C’的坐标( ， )；
(3)、△ABC的面积为 ．19. 已知直线l：y=kx+3经过A、B两点，点A的坐标为(-2，0)．
(1)、求直线l的解析式；
(2)、当kx+3>0时，根据图象直接写出x的取值范围．20. 如图，在△ABC中，AB=AC，AD⊥BC于点D，过点D作DF⊥AB于点F．
(1)、求证：∠ADF= ∠C ；
(2)、若DE是△ACD的中线，∠ADE=55°，求∠BDF的度数．21. 某校为学生装一台直饮水器，课间学生到直饮水器打水．他们先同时打开全部的水龙头放水，后来又关闭了部分水龙头．假设前后两人接水间隔时间忽略不计，且不发生泼洒，直饮水器的余水量y(升)与接水时间x(分)的函数图象如图，请结合图象回答下列问题：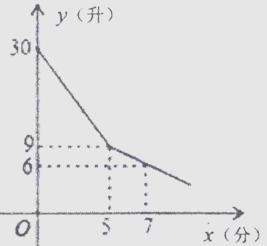
(1)、求当x>5时，y与x之间的函数关系式；(2)、假定每人水杯接水0.7升，要使40名学生接水完毕，课间10分钟是否够用?请计算回答．22. 银杏树具有观赏、经济、药用等价值而深受人们喜爱．在银杏种植基地有A、B两个品种的树苗出售，已知A种比B种每株多20元，买1株A种树苗和2株B种树苗共需200元．(1)、问A、B两种树苗每株分别多少元?(2)、为扩大种植，某农户准备购买A、B两种银杏树苗共36株，且A种树苗数量不少于B种数量的一半，请求出费用最省的购买方案．
23. 如图：在△ABC中，已知∠ABC=45°，过点C作CD⊥AB于点D，过点B作BM⊥AC于点M连接MD，过点D作DN⊥MD，交BM于点N．
(1)、求证：△DBN≌△DCM；(2)、设CD与BM相交于点E，若点E是CD的中点，试探究线段NE、ME、CM之间的数量关系，并证明你的结论．24. 如图，在平面直角坐标系中，直线l1的解析式为y=x，直线l2的解析式为 ，与x轴、y轴分别交于点A、点B，直线l1与l2交于点C．
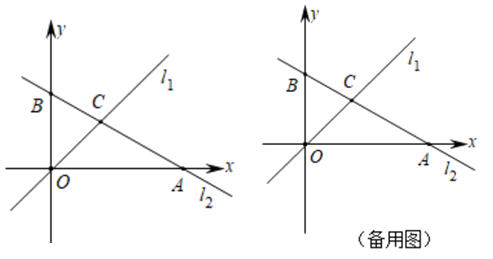(1)、求点A、点B、点C的坐标，并求出△COB的面积；(2)、若直线l2上存在点P(不与B重合)，满足S△COP=S△COB ， 请求出点P的坐标；(3)、在y轴右侧有一动直线平行于y轴，分别与l1 ， l2交于点M、N，且点M在点N的下方，y轴上是否存在点Q，使△MNQ为等腰直角三角形?若存在，请直接写出满足条件的点Q的坐标；若不存在，请说明理由．