广西桂林市2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-03-26 类型:期末考试
一、选择题
-
1. 一元二次方程x2-4=0的解为( )A、x=2 B、x=
 C、x=±
C、x=±  D、x=±2
2. 下列各点中,在反比例函数y=- 的图象上的是( )A、( , 6) B、(- , 6) C、(2,-6) D、(-2,6)3. 为了解某班学生每天的睡眠情况,随机选择该班5名学生进行调查.在一段时间里,平均每人每天的睡眠时间统计如下(单位:小时):6,8,8,7,9.由此估计该班学生平均每人每天的睡眠时间为( )A、7小时 B、7.5小时 C、7.6小时 D、8小时4. 已知 ,那么 的值为( )A、
D、x=±2
2. 下列各点中,在反比例函数y=- 的图象上的是( )A、( , 6) B、(- , 6) C、(2,-6) D、(-2,6)3. 为了解某班学生每天的睡眠情况,随机选择该班5名学生进行调查.在一段时间里,平均每人每天的睡眠时间统计如下(单位:小时):6,8,8,7,9.由此估计该班学生平均每人每天的睡眠时间为( )A、7小时 B、7.5小时 C、7.6小时 D、8小时4. 已知 ,那么 的值为( )A、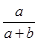 B、
B、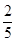 C、
D、
5. 若反比例函数y= 的图象经过点(2,-1),则该函数的图象位于( )A、第一、三象限 B、第三、四象限 C、第一、二象限 D、第二、四象限6. 一元二次方程2x2-3x+1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 在Rt△ACB中,∠C=90°,BC=6,cosA= ,则AC的长为( )A、4.8 B、7.5 C、8 D、108. 现有一个测试距离为5m的视力表(如图),根据这个视力表,小华想制作一个测试距离为3m的视力表,则图中的 的值为( )
C、
D、
5. 若反比例函数y= 的图象经过点(2,-1),则该函数的图象位于( )A、第一、三象限 B、第三、四象限 C、第一、二象限 D、第二、四象限6. 一元二次方程2x2-3x+1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根7. 在Rt△ACB中,∠C=90°,BC=6,cosA= ,则AC的长为( )A、4.8 B、7.5 C、8 D、108. 现有一个测试距离为5m的视力表(如图),根据这个视力表,小华想制作一个测试距离为3m的视力表,则图中的 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、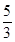 9. 某网店近几年的“双十一”全天交易额逐年稳步增长,已知该网店2016年“双十一”全天交易额为40万元,2018年“双十一”全天交易额为48.4万元,设2016年至2018年该网店“双十一”全天交易额的平均增长率为x,则下列关于x的方程中正确的是( )A、40(1+2x)=48. B、40(1+x)2 =48.4 C、40+40(1+x)+40(1+x)2=48.4 D、40(1+x2)=48.410. 关于x的函数y=k(x+1)和y= (k≠0)在同一坐标系中的图象可能是( )
9. 某网店近几年的“双十一”全天交易额逐年稳步增长,已知该网店2016年“双十一”全天交易额为40万元,2018年“双十一”全天交易额为48.4万元,设2016年至2018年该网店“双十一”全天交易额的平均增长率为x,则下列关于x的方程中正确的是( )A、40(1+2x)=48. B、40(1+x)2 =48.4 C、40+40(1+x)+40(1+x)2=48.4 D、40(1+x2)=48.410. 关于x的函数y=k(x+1)和y= (k≠0)在同一坐标系中的图象可能是( )
A、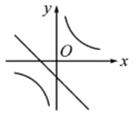 B、
B、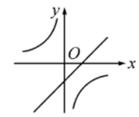 C、
C、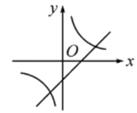 D、
D、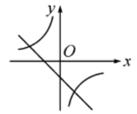 11. 如图,在平面直角坐标系中,已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标为( )
11. 如图,在平面直角坐标系中,已知两点A(2,0),B(0,4),且∠1=∠2,则点C的坐标为( )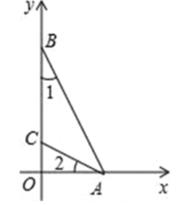 A、(2,0) B、(0,2) C、(1,0) D、(0,1)12. 如图,矩形ABC0的两边OC,OA分别位于x轴,y轴上,点B的坐标为(- ,5),D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,则过点E的反比例函数解析式是( )
A、(2,0) B、(0,2) C、(1,0) D、(0,1)12. 如图,矩形ABC0的两边OC,OA分别位于x轴,y轴上,点B的坐标为(- ,5),D是AB边上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,则过点E的反比例函数解析式是( )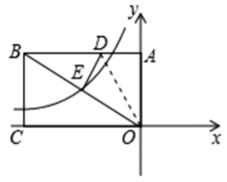 A、
A、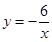 B、
B、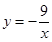 C、
C、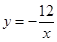 D、
D、
二、填空题.
-
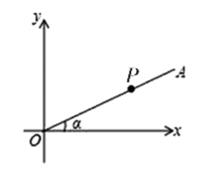
13. 将一元二次方程3x(x-1)=5化为一般形式为14. 若△ABC∽△A’B’C’,且 ,△ABC的周长为12,则△A’B’C’的周长为 .15. 若关于x的方程x2-6x+k=0有两个相等的实数根,则k的值是 .16. 如图,点P是 的OA边上的一点,点P的坐标为(12,5),则tan 等于 .
 17. 反比例函数y= 与y=- 在x轴上方的图象如图所示,点C是y轴正半轴上的一点,过点C作AB∥x轴分别交这两个图象于点A,B.若点P在x轴上,则△ABP的面积等于 .
17. 反比例函数y= 与y=- 在x轴上方的图象如图所示,点C是y轴正半轴上的一点,过点C作AB∥x轴分别交这两个图象于点A,B.若点P在x轴上,则△ABP的面积等于 .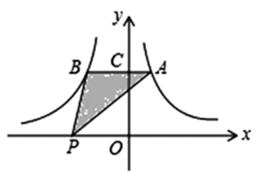 18. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1··按这样的规律进行下去,第2018个正方形的面积为 .
18. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作正方形A1B1C1C;延长C1B1交x轴于点A2 , 作正方形A2B2C2C1··按这样的规律进行下去,第2018个正方形的面积为 .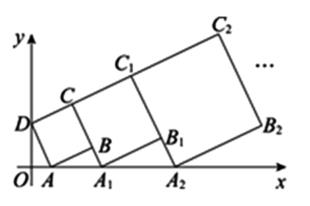
三、解答题
-
19. 计算:|3|+20180+4 sin45°-
20. 解一元二次方程:x2-3x+1=021. 如图,在平面直角坐标系中,A(4,1),B(-1,1).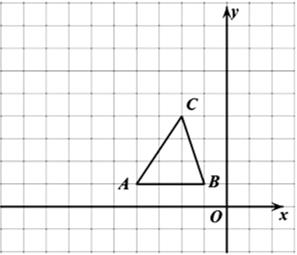 (1)、以O为位似中心,和第二象限内作出△ABC的位似图形△A1B1C1 , 使得△A1B1C1与△ABC的位似比是2:1;(2)、直接写出A1 , B1 , C1的坐标.22. 为了让学生了解消防安全知识,增强消防意识,某市举行了一次共有15000名中学生参加的“消防安全知识竞赛”.为了解本次竞赛成绩情况,从中随机抽取了400名学生的成绩x(得分均为整数,满分为100分)进行统计后得到下表.请根据表格解答下列问题:(1)、请将表格中的数据补充完整;
(1)、以O为位似中心,和第二象限内作出△ABC的位似图形△A1B1C1 , 使得△A1B1C1与△ABC的位似比是2:1;(2)、直接写出A1 , B1 , C1的坐标.22. 为了让学生了解消防安全知识,增强消防意识,某市举行了一次共有15000名中学生参加的“消防安全知识竞赛”.为了解本次竞赛成绩情况,从中随机抽取了400名学生的成绩x(得分均为整数,满分为100分)进行统计后得到下表.请根据表格解答下列问题:(1)、请将表格中的数据补充完整;分组
频数
频率
51≤x<61
40
10%
61≤x<71
15%
71≤x<81
100
81≤x<91
120
30%
91≤x<101
合计
400
100%
(2)、假设成绩在71分至91分之间(含71分不含91分)的学生为二等奖,请估计该市获得二等奖的学生人数.23. 如图,某校数学兴趣小组的同学欲测量与地面垂直的旗杆BD的高度,他们先在A处测得旗杆顶端点D的仰角为45°,再沿着BA的方向前进10米至C处,测得旗杆顶端点D的仰角为30°.求该旗杆BD的高度(结果保留根号).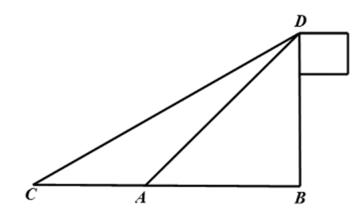 24. 如图,某校准备一面利用墙,其余—面用篱笆围成一个矩形花辅ABCD.已知旧墙可利用的最大长度为13 m,篱笆长为24 m,设垂直于墙的AB边长为xm.
24. 如图,某校准备一面利用墙,其余—面用篱笆围成一个矩形花辅ABCD.已知旧墙可利用的最大长度为13 m,篱笆长为24 m,设垂直于墙的AB边长为xm.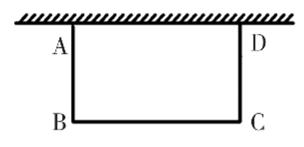 (1)、若围成的花圃面积为70m 2时,求BC的长;
(1)、若围成的花圃面积为70m 2时,求BC的长;
(2)、如图,若计划将花圃中间用一道篱笆隔成两个小矩形,且花圃面积为78 m2 , 请你判断能否围成这样的花圃?如果能,求BC的长;如果不能,请说明理由.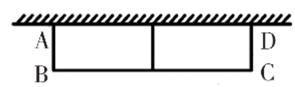 25. 已知:如图,在平面直角坐标系中,直线AB分别与x,y轴交于点B,A,与反比例函数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=8,OE=4.
25. 已知:如图,在平面直角坐标系中,直线AB分别与x,y轴交于点B,A,与反比例函数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=8,OE=4.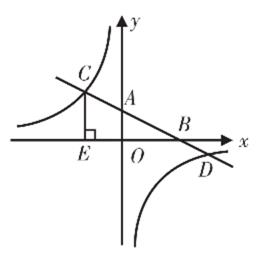 (1)、求BC的长;(2)、求反比例函数的解析式;(3)、连接ED,求tan∠BED.26. 如图,有一边长为5cm的正方形ABCD和等腰△PQR,PQ =PR=5cm,QR=8cm,点B、Q、C、R在同一直线l上,当Q、C两点重合时,等腰△PQR以每秒1cm的速度沿直线l按箭头所示的方向开始匀速运动,设t秒后正方形ABCD与等腰△PQR重叠部分的面积为S.
(1)、求BC的长;(2)、求反比例函数的解析式;(3)、连接ED,求tan∠BED.26. 如图,有一边长为5cm的正方形ABCD和等腰△PQR,PQ =PR=5cm,QR=8cm,点B、Q、C、R在同一直线l上,当Q、C两点重合时,等腰△PQR以每秒1cm的速度沿直线l按箭头所示的方向开始匀速运动,设t秒后正方形ABCD与等腰△PQR重叠部分的面积为S.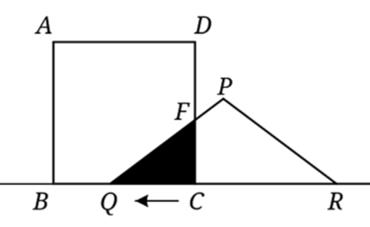 (1)、填空:当t=秒时,DC平分PQ;(2)、当0<t<4时,设PQ与DC交于点F,求FC(用含t的代数式表示).(3)、当8≤t≤13时,求S关于t的函数表达式.
(1)、填空:当t=秒时,DC平分PQ;(2)、当0<t<4时,设PQ与DC交于点F,求FC(用含t的代数式表示).(3)、当8≤t≤13时,求S关于t的函数表达式.