浙江省台州市2019届九年级上学期数学教学质量检测(二)
试卷更新日期:2019-03-26 类型:期末考试
一、单选题
-
1. 下列事件属于随机事件的是( )A、任意画一个三角形,其内角和为 180° B、掷一次骰子,向上一面点数是 7 C、经过有交通信号灯的路口,遇到红灯 D、明天的太阳从东方升起2. 如图,将直角三角板 60°角的顶点放在圆心 O 上,斜边和一直角边分别与⊙O 相交于A,B 两点,P 是优弧 AB 上任意一点(与 A,B 不重合),则∠APB=( )
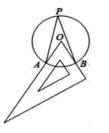 A、15° B、30° C、45° D、60°3. 在圆内接四边形ABCD中,∠A:∠B:∠C:∠D的度数之比可能是( )A、1:2:3:4 B、4:2:1:3 C、4:2:3:1 D、1:3:2:44. 如图,在△ABC 中,∠ACB=90°,∠A=30°,AB=4,以点 B 为圆心,BC 长为半径画弧, 交边 AB 于点 D,则 的长为( )
A、15° B、30° C、45° D、60°3. 在圆内接四边形ABCD中,∠A:∠B:∠C:∠D的度数之比可能是( )A、1:2:3:4 B、4:2:1:3 C、4:2:3:1 D、1:3:2:44. 如图,在△ABC 中,∠ACB=90°,∠A=30°,AB=4,以点 B 为圆心,BC 长为半径画弧, 交边 AB 于点 D,则 的长为( )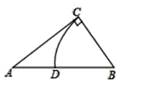 A、
A、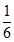 p
B、
p
B、 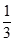 p
C、
p
C、 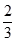 p
D、
p
D、 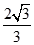 p
5. 2018年某市初中学业水平实验操作考试.要求每名学生从物理、化学、生物三个学科中随机抽取一科参加测试,小华和小强都抽到物理学科的概率是( )A、
p
5. 2018年某市初中学业水平实验操作考试.要求每名学生从物理、化学、生物三个学科中随机抽取一科参加测试,小华和小强都抽到物理学科的概率是( )A、 B、
C、
B、
C、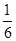 D、
6. 从一个半径为 10 的圆形纸片上裁出一个最大的正六边形,此正六边形的边心距是( )
D、
6. 从一个半径为 10 的圆形纸片上裁出一个最大的正六边形,此正六边形的边心距是( )
A、5 B、10 C、5 D、107. 如图,用一块直径为 a 的圆桌布平铺在对角线长为 a 的正方形桌面上,若四周下垂的最 大长度相等,则桌布下垂的最大长度 x 为( )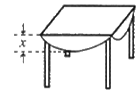 A、
A、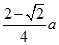 B、
B、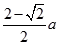 C、
C、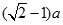 D、
D、 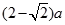 8. 已知,如图,点 C、D 在⊙O 上,直径 AB=6 cm,弦 AC,BD 相交于点 E.若 CE=BC, 则阴影部分面积为( )
8. 已知,如图,点 C、D 在⊙O 上,直径 AB=6 cm,弦 AC,BD 相交于点 E.若 CE=BC, 则阴影部分面积为( )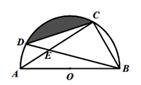 A、p -
A、p - B、
B、 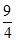 p -
p -  C、
C、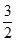 p -
p -  D、
D、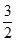 p -
p -  9. 如图,PA,PB分别切⊙O于A,B两点,射线PD与⊙O相交于C,D两点,点E是CD中点,若∠APB=40°,则∠AEP的度数是( )
9. 如图,PA,PB分别切⊙O于A,B两点,射线PD与⊙O相交于C,D两点,点E是CD中点,若∠APB=40°,则∠AEP的度数是( )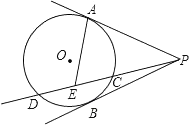 A、40° B、50° C、60° D、70°10. 如图,在 5×5 的网格中,每个小正方形的边长都是 1 个单位长度,网格中小正方形的顶 点叫格点,矩形 ABCD 的边分别过格点 E,F,G,H,则当 OD 取最大值时,矩形 ABCD 的面积为( )
A、40° B、50° C、60° D、70°10. 如图,在 5×5 的网格中,每个小正方形的边长都是 1 个单位长度,网格中小正方形的顶 点叫格点,矩形 ABCD 的边分别过格点 E,F,G,H,则当 OD 取最大值时,矩形 ABCD 的面积为( )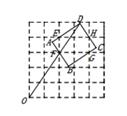 A、4 B、
A、4 B、 C、5
D、
C、5
D、 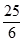
二、填空题
-
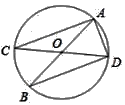
11. 如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是 .
 12. 如图,四边形 ABCD 内接于⊙O ,AB 为⊙O 的直径,点 C 为弧 BD 的中点.若∠DAB=40°,则∠ABC= .
12. 如图,四边形 ABCD 内接于⊙O ,AB 为⊙O 的直径,点 C 为弧 BD 的中点.若∠DAB=40°,则∠ABC= . 13. 小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正那赢;如 果两次是一正一反,则我嬴.”小红赢的概率是 ,据此判断该游戏 (填“公平”或“不公平”).14. 如图,点 A 在以 BC 为直径的⊙O 内,且 AB=AC,以点 A 为圆心,AC 长为半径作弧, 得到扇形 ABC,剪下扇形 ABC 围成一个圆锥(AB 和 AC 重合),若∠ABC=30°, BC = 2 ,则这个圆锥底面圆的半径是 .
13. 小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正那赢;如 果两次是一正一反,则我嬴.”小红赢的概率是 ,据此判断该游戏 (填“公平”或“不公平”).14. 如图,点 A 在以 BC 为直径的⊙O 内,且 AB=AC,以点 A 为圆心,AC 长为半径作弧, 得到扇形 ABC,剪下扇形 ABC 围成一个圆锥(AB 和 AC 重合),若∠ABC=30°, BC = 2 ,则这个圆锥底面圆的半径是 . 15. 如图,在△ABC 中,∠A=70°,⊙O 截△ABC 的三边所得弦长相等,则∠BOC 的度数为 .
15. 如图,在△ABC 中,∠A=70°,⊙O 截△ABC 的三边所得弦长相等,则∠BOC 的度数为 .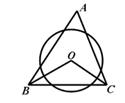 16. 如图,正三角形 ABC 的边长为 1,点 P 从 B 点出发沿 B- C 运动至点以 C,点 Bʹ是点 B
16. 如图,正三角形 ABC 的边长为 1,点 P 从 B 点出发沿 B- C 运动至点以 C,点 Bʹ是点 B关于直线 AP 对称的点.
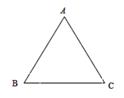 (1)、点 P 从点 B 运动至 C 过程中,下列说法正确的有 . (填序号)
(1)、点 P 从点 B 运动至 C 过程中,下列说法正确的有 . (填序号)①当点 P 运动到 C 时,线段 AP 长为 1;②点 Bʹ沿直线从 B 运动到 Bʹ;
③点 Bʹ沿圆弧从 B 运动到 Bʹ
(2)、点 P 从点 B 运动至 C 的过程中,点 Bʹ从起点到终点的运动路程的长是 .三、解答题
-
17. 如图,AB 是⊙O 的直径,∠ACD=25°,求∠BAD 的度数.
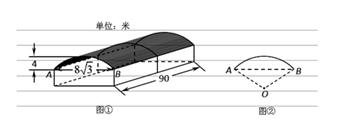
 18. 为保护共享单车,图①是某工厂门口修建的存放自行车的车棚示意图(尺寸如 图所示).车棚顶部是圆柱侧面的一部分,其展开图是矩形.图②是车棚顶部截面的示 意图,弧 AB 所在圆的圆心为 O.车棚顶部是用铝合金覆盖的,求所用铝合金的面积
18. 为保护共享单车,图①是某工厂门口修建的存放自行车的车棚示意图(尺寸如 图所示).车棚顶部是圆柱侧面的一部分,其展开图是矩形.图②是车棚顶部截面的示 意图,弧 AB 所在圆的圆心为 O.车棚顶部是用铝合金覆盖的,求所用铝合金的面积(不考虑接缝等因素,计算结果保留 π).
 19. “智创”学习机制造公司对一批学习机质量抽检情况如下:
19. “智创”学习机制造公司对一批学习机质量抽检情况如下: (1)、填写表格中正品的频率.(2)、从这批学习机中任选一个是次品的概率约为多少?(3)、这批学习机有 5000 个,估计其中次品大约有多少个?20. 如图,在⊙O 中,AB 是直径,AD 是弦,∠ADE=60°,∠C=30°.
(1)、填写表格中正品的频率.(2)、从这批学习机中任选一个是次品的概率约为多少?(3)、这批学习机有 5000 个,估计其中次品大约有多少个?20. 如图,在⊙O 中,AB 是直径,AD 是弦,∠ADE=60°,∠C=30°.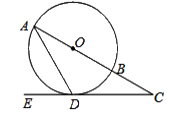 (1)、判断直线 CD 是否为⊙O 的切线,并说明理由;(2)、若 CD = 3 ,求 BC 的长.21. 如图,AB=16,O 为 AB 中点,点 C 在线段 OB 上(不与点 O,B 重合),将 OC 绕点 O 逆时针旋转 270°后得到扇形 COD,AP,BQ 分别切优弧 CD 于点 P,Q,且 点 P,Q 在 AB 两侧,连接 OP.
(1)、判断直线 CD 是否为⊙O 的切线,并说明理由;(2)、若 CD = 3 ,求 BC 的长.21. 如图,AB=16,O 为 AB 中点,点 C 在线段 OB 上(不与点 O,B 重合),将 OC 绕点 O 逆时针旋转 270°后得到扇形 COD,AP,BQ 分别切优弧 CD 于点 P,Q,且 点 P,Q 在 AB 两侧,连接 OP.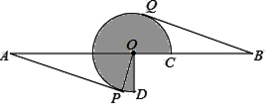 (1)、求证:AP=BQ;(2)、当 BQ =4 时,求优弧 QD 的长(结果保留 π);(3)、若△APO 的外心在扇形 COD 的内部,求 OC 的取值范围.22. 如图,已知正方形 ABCD 的边长是 5,点 O 在 AD 上,OD=2,且⊙O 的直径 是 4.
(1)、求证:AP=BQ;(2)、当 BQ =4 时,求优弧 QD 的长(结果保留 π);(3)、若△APO 的外心在扇形 COD 的内部,求 OC 的取值范围.22. 如图,已知正方形 ABCD 的边长是 5,点 O 在 AD 上,OD=2,且⊙O 的直径 是 4.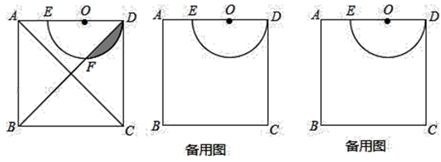 (1)、正方形的对角线 BD 与半圆 O 交于点 F,求阴影部分的面积;(2)、利用图判断,半圆 O 与 AC 有没有公共点,说明理由.(提示: » 1.41 )
(1)、正方形的对角线 BD 与半圆 O 交于点 F,求阴影部分的面积;(2)、利用图判断,半圆 O 与 AC 有没有公共点,说明理由.(提示: » 1.41 )
(3)、将半圆 O 以点 E 为中心,顺时针方向旋转.①旋转过程中,△BOC 的最小面积是;
②当半圆 O 过点 A 时,半圆 O 位于正方形以外部分的面积是 .
23. 如图,点 A、B、C 是半径为 2 的半圆 O 上的三个点,点 A 是 B»C 的中点,连 接 AB、AC,点 D、E 分别在弦 AB、AC 上,且满足 AD=CE. (1)、求证: OD=OE;(2)、连接 BC,当 BC = 2 时,求∠DOE 的度数;(3)、若∠BAC=120°,当点 D 在弦 AB 上运动时,四边形 ADOE 的面积是否变化?若变化,请说明理由;若不变化,请求出四边形 ADOE 的面积.
(1)、求证: OD=OE;(2)、连接 BC,当 BC = 2 时,求∠DOE 的度数;(3)、若∠BAC=120°,当点 D 在弦 AB 上运动时,四边形 ADOE 的面积是否变化?若变化,请说明理由;若不变化,请求出四边形 ADOE 的面积.
24. 已知矩形 ABCD 内接于⊙O,AB=6 cm,AD=8 cm,以圆心 O 为旋转中心,把 矩形 ABCD 顺时针旋转,得到矩形 A′B′C′D′仍然内接于⊙O,记旋转角为 α(0°<α≤90°).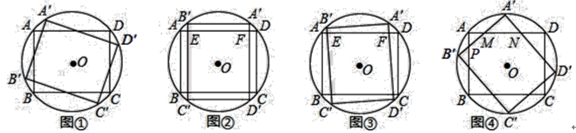 (1)、如图①,⊙O 的直径为cm;(2)、如图②,当 α=90°时,B′C′与 AD 交于点 E,A′D′与 AD 交于点 F,则四边形 A′B′EF 的 周长是cm.(3)、如图③,B′C′与 AD 交于点 E,A′D′与 AD 交于点 F,比较四边形 A′B′EF 的周长和⊙O的直径的大小关系;
(1)、如图①,⊙O 的直径为cm;(2)、如图②,当 α=90°时,B′C′与 AD 交于点 E,A′D′与 AD 交于点 F,则四边形 A′B′EF 的 周长是cm.(3)、如图③,B′C′与 AD 交于点 E,A′D′与 AD 交于点 F,比较四边形 A′B′EF 的周长和⊙O的直径的大小关系;
(4)、如图④,若 A′B′与 AD 交于点 M,与 AB 交于点 P,A′D′与 AD 交于点 N,当旋转角α=度时,△A′MN 是等腰三角形,并求出△A′MN 的周长.