浙江省台州市2018-2019学年七年级上学期数学教学质量检测（二）
试卷更新日期：2019-03-26 类型：期末考试
一、单选题
-
1. 下列等式是一元一次方程的是（ ）A、
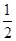x2 + 1 = 0
B、 x + 1 = 
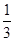C、x + y = 0
D、2 -1=-3 +4
2. 方程 2x－4=0 的解是（ ）A、x=－2 B、x=0 C、x=2 D、 x=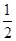
3. 下列四组变形中，变形正确的是（ ）A、 由 5x+7=0 得 5x=－7 B、由 2x－3=0 得 2x－3+3=0 C、由得
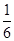x=2，得 x=
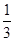D、由 5x=7 得 x=35
4. 如果 am=an，那么下列等式不一定成立的是（ ）A、am－3=an－3 B、m=n C、5+am=5+an D、
am= an
5. “△”表示一种运算符号，其意义是：a△b=2a－b，如果 x△(1△3)=2，那么 x 等于（ ）
A、1 B、
C、
D、2
6. 某商店有两个进价不同的计算器都卖了80元，其中一个赢利60%，另一个亏本20%，在这次买卖中，这家商店( )A、不赔不赚 B、赚了10元 C、赔了10元 D、赚了50元7. 已知关于 x 的方程 3x+m=5 的解为 x=2，则关于 y 的方程 3(y－2)+m=5 的解为（ ）
A、y=-1 B、y=0 C、y=2 D、y=48. 如图，所有圆柱体的质量均相等，且两架天平都保持平衡，则 5 个小球的质量相当于（ ） 正方体的质量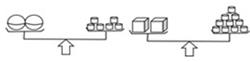
A、2 个 B、3 个 C、4 元 D、5 个9. 如图是一块在电脑屏幕上出现的矩形色块图，由 6 个不同颜色的正方形组成，已知中 间最小的一个正方形的边长为 1，那么这个矩形色块图的面积为（ ）
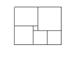A、142 B、143 C、144 D、14510. 有 m 辆校车及 n 名学生，若每辆校车乘坐 40 名学生，则还有 10 名学生不能上车；若每 辆校车乘坐 43 名学生，则只有 1 名学生不能上车．现有下列四个方程：①40m+10=43m－1；② = ；③ = ；④40m+10=43m+1．
其中正确的是( )
A、①② B、②④ C、②③ D、③④二、填空题
-
11. 请写出一个解为 x=3 的一元一次方程 ．12. 若 x=2 是关于 x 的一元一次方程 2x－a=3 的解，则 a= ．13. 三个连续奇数的和是 75，这三个数分别是 ．14. 一家商店将某种服装按成本价提高 40%后标价，又以 8 折优惠卖出，结果每件仍获利15 元，这种服装每件的成本为元 ．
15. 若方程 2(2x－1)=3x+1 与方程 m=x－1 的解相同，则 m 的值为 ．16. 轮船沿江从A港顺流行驶到B港，比从B港返回A港少用3小时，若船速为26千米/小时，水速为2千米/时，则A港和B港相距千米．17. 定义：若关于 x 的一元一次方程 ax=b（其中 a≠0，b≠0）的解为 x = ，则称方程 ax=b为 “商解方程”，例如，3x=－3 就是一个“商解方程”．若关于 x 的一元一次方程(m－2)x=4 是一个“商解方程”，则 m 的值为 ．
18. 如图，若开始输入的x的值为正整数，最后输出的结果为144，则满足条件的 的值为 ．
三、解答题
-
19. 解方程：(1)、10 - x = 3x - 2(2)、 = 1 - ．20. 小明解方程 + 1 = 时，由于粗心大意，在去分母时，方程左边的 1 没有乘 10，由此求得的解为 x=4，试求 a 的值，并求出方程正确的解．21. 某校组织师生春游活动，如果每辆车坐 45 人，那么还剩 20 人没有座位；如果每辆车坐 55 人，那么会有 30 个空座位．此次春游活动中共有几辆车？有多少名学生？22. 甲、乙两工程队承建某校校园绿化工程，已知甲队单独完成需要 9 天，乙队单独 完成需要 18 天．(1)、若先由甲、乙两队合做 4 天，剩下工程由乙队单独完成，则还需几天可完成此项 工程？(2)、在(1)的条件下，工程结束后学校共支付 90 000 元工程款，若按甲、乙两队完成的工作量分配这笔钱，问甲、乙两队各得到多少元工程款？
23. 某水果店用 1000 元购进甲、乙两种新出产的水果共 140 千克，这两种水果的进 价、售价如表所示：进价（元/千克）
售价（元/千克）
甲种
5
8
乙种
9
13
(1)、这两种水果各购进多少千克？(2)、若该水果店按售价售完这批水果，获得的利润是多少元？(3)、如果这批水果是在一天之内按照售价销售完成的，除了进货成本，水果店每天的其 他销售费用是 0.1 元/千克，那么水果店销售这批水果获得的利润是多少元？24. 以下两幅图有两个探究活动(1)、图 1 中的两位同学编了两个数字谜题．如果每个题中的“□”表示同一个数字，那么 谜题中的“□”分别是： ， ．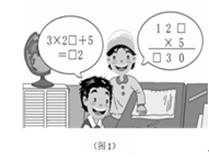
(2)、图 2 中，阿童木说：“把我的出生月份数乘以 2，加 8，再把和乘 5，加上我家的人口数，我家人口不到 10 人，结果为 134”．阿童木的出生月份是；他家 有口人 ．
(3)、试利用以上两小题的解答经验，解决以下问题：一个三位数的个位数字为 3，若把 3 放在百位，其他两个数字顺序不变得到一个新三 位数，而此新三位数的 2 倍比原数大 5．则原来的三位数是多少？
25. 某书城开展学生优惠购书活动：凡一次性购书不超过 200 元的一律九折优惠，超 过 200 元的，其中 200 元按九折算，超过 200 元的部分按八折算．(1)、甲同学一次性购书标价的总和为 120 元，需付款元．(2)、乙同学一次性购书标价的总和为 x 元(x>200)，需付款元．(3)、丙同学第一次去购书付款 81 元，第二次去购书享受了八折优惠，他查看了所买书的标价，发现两次共节约了 41 元，则该学生第二次购书实际付款多少元？
26. 动点 A 从原点出发向数轴负方向运动，同时，动点 B 也从原点出发向数轴正方 向运动，4 秒后，两点相距 16 个单位长度．已知动点 A、B 的速度比为 1∶3（速度单 位：单位长度/秒）．
(1)、求出两个动点运动的速度，并在数轴上标出 A、B 两点运动 4 秒后的位置；(2)、若 A、B 两点从(1)中标出的位置同时出发，均按原速度向数轴负方向运动，求几秒钟 后两个动点相距 8 个单位长度；(3)、当 A、B 两点从(1)中标出的位置出发向数轴负方向运动时，另一动点 C 也同时从原 点的位置出发向 A 运动，当遇到 A 后立即返回向 B 点运动，遇到 B 后又立即返回向 A 运动，如此往返，直到 B 追上 A 时，C 立即停止运动．若点 C 一直以 5 单位长度/ 秒的速度匀速运动，则点 C 一共运动了 个单位长度．