浙江省温州市2018-2019学年九年级下学期数学百题竞赛试卷
试卷更新日期:2019-03-26 类型:竞赛测试
一、选择题
-
1. -9的绝对值是( )A、-9 B、9 C、±9 D、-
 2. 点P(3,-2)在平面直角坐标系中所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知⊙O的半径为4,点P在⊙O内,则OP的长可能是( )A、3 B、4 C、5 D、64. 下列运算正确的是( )A、(a2)3=a5 B、a2·a4=a8 C、a6÷a3=a2 D、(ab)3=a3b35. 如图,在▱ABCD中,∠B=64°,则∠D=( )
2. 点P(3,-2)在平面直角坐标系中所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知⊙O的半径为4,点P在⊙O内,则OP的长可能是( )A、3 B、4 C、5 D、64. 下列运算正确的是( )A、(a2)3=a5 B、a2·a4=a8 C、a6÷a3=a2 D、(ab)3=a3b35. 如图,在▱ABCD中,∠B=64°,则∠D=( )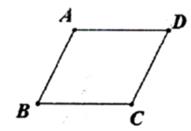 A、26° B、32° C、64° D、116°6. 一元一次不等式x+1>2的解在数轴上表示为( )A、
A、26° B、32° C、64° D、116°6. 一元一次不等式x+1>2的解在数轴上表示为( )A、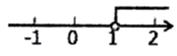 B、
B、 C、
C、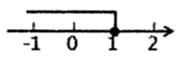 D、
D、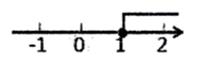 7. 将一把长方形的直尺与一块直角三角板如图放置,若∠1=45°,则∠2为( )
7. 将一把长方形的直尺与一块直角三角板如图放置,若∠1=45°,则∠2为( )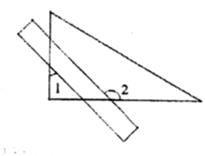 A、115° B、120° C、135° D、145°8. 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )A、3 B、 C、 D、9. 下列实数中,有理数是( )A、sin 45° B、
A、115° B、120° C、135° D、145°8. 在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠A的正切值为( )A、3 B、 C、 D、9. 下列实数中,有理数是( )A、sin 45° B、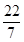 C、
C、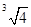 D、
10. 在△ABC,AB=1,AC= ,BC= ,则该三角形为( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形11. 是二元一次方程mx+y-1=0的一组解,则m的解为( )A、- B、 C、 D、-12. 二次函数y=-(x-1)2+2图象的对称轴是( )A、直线x=2 B、直线x=1 C、直线x=-1 D、直线x=-213. 下列图形中,是中心对称图形的是( )A、
D、
10. 在△ABC,AB=1,AC= ,BC= ,则该三角形为( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形11. 是二元一次方程mx+y-1=0的一组解,则m的解为( )A、- B、 C、 D、-12. 二次函数y=-(x-1)2+2图象的对称轴是( )A、直线x=2 B、直线x=1 C、直线x=-1 D、直线x=-213. 下列图形中,是中心对称图形的是( )A、 B、
B、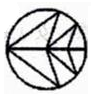 C、
C、 D、
D、 14. 数轴上表示 的点A的位置在( )A、1与2之间 B、2与3之间 C、3与4之间 D、4与5之间15. 一个不透明的布袋里装有5个红球,2个白球,3个黄球,它们除颜色外其余都相同,从袋中任意摸出1个球,是黄球的概率为( )A、 B、 C、
14. 数轴上表示 的点A的位置在( )A、1与2之间 B、2与3之间 C、3与4之间 D、4与5之间15. 一个不透明的布袋里装有5个红球,2个白球,3个黄球,它们除颜色外其余都相同,从袋中任意摸出1个球,是黄球的概率为( )A、 B、 C、 D、
D、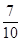 16. 已知矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD相似的是( )A、
16. 已知矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD相似的是( )A、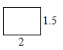 B、
B、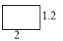 C、
C、 D、
D、 17. 已知 (a≠0,b≠0),下列变形错误的是( )A、 B、2a=3b C、
17. 已知 (a≠0,b≠0),下列变形错误的是( )A、 B、2a=3b C、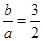 D、3a=2b
18. 如图,等边△OAB的边长为2,则点B的坐标为( )
D、3a=2b
18. 如图,等边△OAB的边长为2,则点B的坐标为( )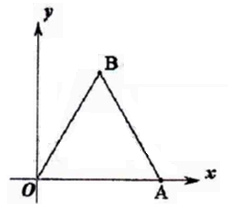 A、(1,1) B、( ,1) C、( , ) D、(1, )19. 对假命题“若a>b,则a2>b2”举反例, 正确的反例是( )A、a=-1,b=0 B、a=-1,b=-1 C、a=-1,b=-2 D、a=-1,b=220. 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,此时海轮航行的距离AB长是( )
A、(1,1) B、( ,1) C、( , ) D、(1, )19. 对假命题“若a>b,则a2>b2”举反例, 正确的反例是( )A、a=-1,b=0 B、a=-1,b=-1 C、a=-1,b=-2 D、a=-1,b=220. 如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向,此时海轮航行的距离AB长是( )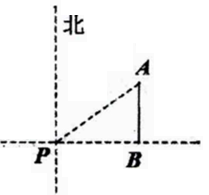 A、2海里 B、2sin55°海里 C、2cos55°海里 D、2tan55°海里21. 如图,这是一个机械模具,则它的俯视图是( )
A、2海里 B、2sin55°海里 C、2cos55°海里 D、2tan55°海里21. 如图,这是一个机械模具,则它的俯视图是( )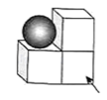 A、
A、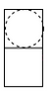 B、
B、 C、
C、 D、
D、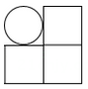 22. 若反比例函数y= 的图象经过点(-3,4),则它的图象也一定经过的点是( )A、(-4,-3) B、(-3,-4) C、(2,-6) D、(6,2)23. 为了绿化校园,30名学生共种80棵树苗.其中男生每人种3棵,女生每人种2棵,该班男生有x人,女生有y人.根据题意,所列方程组正确的是( )A、
22. 若反比例函数y= 的图象经过点(-3,4),则它的图象也一定经过的点是( )A、(-4,-3) B、(-3,-4) C、(2,-6) D、(6,2)23. 为了绿化校园,30名学生共种80棵树苗.其中男生每人种3棵,女生每人种2棵,该班男生有x人,女生有y人.根据题意,所列方程组正确的是( )A、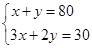 B、
B、 C、
C、 D、
D、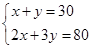 24. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )
24. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的大小为( )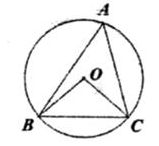 A、40° B、50° C、80° D、100°25. 不等式2-3x≥2x-8的非负整数解有( )A、1个 B、2个 C、3个 D、4个26. 下列事件中,是必然事件的是( )A、秀秀打开电视,正在播放广告 B、掷一枚质地均匀的硬币,一定正面向上 C、如果a2=b2 , 那么a=b D、任意画一个n边形,其n个不共顶点的外角和是360°27. 如图将△ABC绕点A顺时针旋转90°得到△AED,若点B,D,E在同一条直线上,∠BAC=20°,则∠ADB的度数为( )
A、40° B、50° C、80° D、100°25. 不等式2-3x≥2x-8的非负整数解有( )A、1个 B、2个 C、3个 D、4个26. 下列事件中,是必然事件的是( )A、秀秀打开电视,正在播放广告 B、掷一枚质地均匀的硬币,一定正面向上 C、如果a2=b2 , 那么a=b D、任意画一个n边形,其n个不共顶点的外角和是360°27. 如图将△ABC绕点A顺时针旋转90°得到△AED,若点B,D,E在同一条直线上,∠BAC=20°,则∠ADB的度数为( )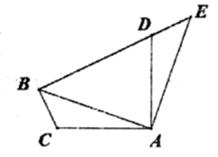 A、55° B、60° C、65° D、70°28. 用配方法解方程x2-4x=1,配方后所得的方程是( )A、(x-2)2=5 B、(x+2)2=5 C、(x-2)2=3 D、(x+2)2=329. 把一张长方形纸片按如图①,图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
A、55° B、60° C、65° D、70°28. 用配方法解方程x2-4x=1,配方后所得的方程是( )A、(x-2)2=5 B、(x+2)2=5 C、(x-2)2=3 D、(x+2)2=329. 把一张长方形纸片按如图①,图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )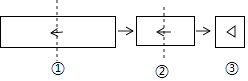 A、
A、 B、
B、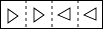 C、
C、 D、
D、 30. 我校七年级开展了“你好!阅读“的读书话动。为了解全段699名学生的读书情况,随机调查了本年级50名学生平均每月读书的册数,统计数据如下表所示:关于这组数据,下列说法正确的是( )
30. 我校七年级开展了“你好!阅读“的读书话动。为了解全段699名学生的读书情况,随机调查了本年级50名学生平均每月读书的册数,统计数据如下表所示:关于这组数据,下列说法正确的是( )册数
0
1
2
3
4
人数
4
12
16
17
1
A、中位数是2 B、众数是17 C、平均数是2 D、方差是231. 如图是由8个全等的小矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )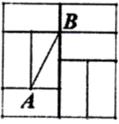 A、2个 B、3个 C、4个 D、5个32. 山山从家到书店买书后返回,他离家的距离y(拥)与离家的时间x(分钟)之间的对应关系如图所示,若山山在书店买书30分钟,则他离家50分钟时离家的距离为( )
A、2个 B、3个 C、4个 D、5个32. 山山从家到书店买书后返回,他离家的距离y(拥)与离家的时间x(分钟)之间的对应关系如图所示,若山山在书店买书30分钟,则他离家50分钟时离家的距离为( )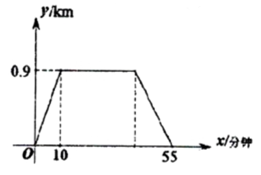 A、0.06km B、0.3km C、0.6km D、0.9km33. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、0.06km B、0.3km C、0.6km D、0.9km33. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( ) A、15 B、30 C、45 D、6034. 已知A,B,C三点在同一条直线上,M,N分别为线段AB,BC的中点.且AB=80,BC=60,则MN的长为( )A、10 B、70 C、10或70 D、30或7035. 如图,在△ABC中,延长BC至D,使得CD= BC,过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
A、15 B、30 C、45 D、6034. 已知A,B,C三点在同一条直线上,M,N分别为线段AB,BC的中点.且AB=80,BC=60,则MN的长为( )A、10 B、70 C、10或70 D、30或7035. 如图,在△ABC中,延长BC至D,使得CD= BC,过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )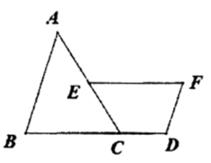 A、3 B、4 C、 D、
A、3 B、4 C、 D、 36. 如图,平面直角坐标系中,已知点P(2,2),C为y轴正半轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴。垂足为B,直线AB与直线OP交于点A,且BD=4AD,线段CD与直线DP交于点Q,则点Q的坐标为( )
36. 如图,平面直角坐标系中,已知点P(2,2),C为y轴正半轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴。垂足为B,直线AB与直线OP交于点A,且BD=4AD,线段CD与直线DP交于点Q,则点Q的坐标为( )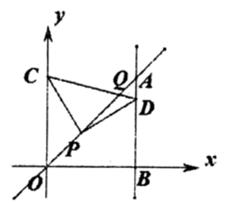 A、(4,4) B、(
A、(4,4) B、(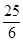 ,
, 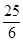 )
C、(
)
C、( 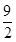 ,
, 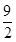 )
D、(
)
D、(  ,
,  )
37. 按一定规律排列的一列数依次为:2,3,10,15,26,35,…,按此规律排列下去,则这列数中的第 100 个数是( )A、9999 B、10000 C、10001 D、1000238. 一种包装盒的设计方法如图所示,四边形ABCD是边长为30cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=xcm,要使包装盒的侧面积最大,则x应取( )
)
37. 按一定规律排列的一列数依次为:2,3,10,15,26,35,…,按此规律排列下去,则这列数中的第 100 个数是( )A、9999 B、10000 C、10001 D、1000238. 一种包装盒的设计方法如图所示,四边形ABCD是边长为30cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=xcm,要使包装盒的侧面积最大,则x应取( )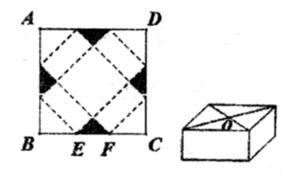 A、12.5cm B、10cm C、7.5cm D、5cm39. 如图,抛物线y=-x2+k与x轴交于A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△ADC和等腰△BEC,点D,E恰好落在此抛物线上,在整个运动过程中, ∠DCE的变化情况是( )
A、12.5cm B、10cm C、7.5cm D、5cm39. 如图,抛物线y=-x2+k与x轴交于A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△ADC和等腰△BEC,点D,E恰好落在此抛物线上,在整个运动过程中, ∠DCE的变化情况是( )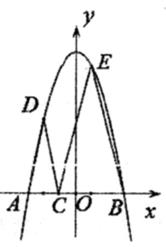 A、保持不变 B、一直减小 C、先增大后减小 D、先减小后增大40. 甲、乙两人玩纸牌游戏,从足够数量的纸牌中取牌.规定每人最多两种取法,甲每次取4张或(4-k)张,乙每次取6张或(6-k)张(七是常数,0<k<4).经统计。甲共取了15次,乙共取了17次,并且乙至少取了一次6张牌,最终两人所取牌的总张数恰好相等,那么纸牌最少有( )张.A、 162 B、114 C、108 D、102
A、保持不变 B、一直减小 C、先增大后减小 D、先减小后增大40. 甲、乙两人玩纸牌游戏,从足够数量的纸牌中取牌.规定每人最多两种取法,甲每次取4张或(4-k)张,乙每次取6张或(6-k)张(七是常数,0<k<4).经统计。甲共取了15次,乙共取了17次,并且乙至少取了一次6张牌,最终两人所取牌的总张数恰好相等,那么纸牌最少有( )张.A、 162 B、114 C、108 D、102二、填空题
-
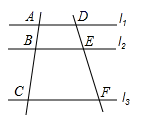
41. 计算:(-3)3= .42. 2019年春节期间,电影《流浪地球》受到众多影迷的追捧,据猫眼实时数据统计大年初二全天的综合票房大约262000000元。数据262000000用科学记数法表示为 .43. 一个多边形的内角和为900°,这个多边形的边数是 .44. 因式分解:4m2n-n= .45. 如果二次根式 有意义,那么x的取值范围是 .46. 已知关于x的_元二次方程x2+3x+m=0有两个相等的实数根,则m= .47. 如图,直线l1∥l2∥l3 , 直线AC交l1 , l2 , l3于点A,B,C; 直线DF交l1 , l2 , l3 , 于点D,E,F,已知 ,则 = .
 48. 方程(2x+1)2=49的根是 .49. 如图,点A,B,C在同一条直线上,∠A=∠DBE=∠C=90°,请你只添加一个条件 , 使得△DAB≌△BCE.
48. 方程(2x+1)2=49的根是 .49. 如图,点A,B,C在同一条直线上,∠A=∠DBE=∠C=90°,请你只添加一个条件 , 使得△DAB≌△BCE.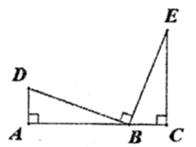 50. 在半径为3的圆中,80°的圆心角所对的弧长是 .51. 若多项式2x2+3x-7的值为-10,则多项式6x2+9x+7的值为 .52. 若点(-1,y1)与(2,y2)在一次函数y=-2x+1的图象上,则y1y2(填>、<或=).53. 如图是正方体的表面展开图。则与“学”字相对的字是 .
50. 在半径为3的圆中,80°的圆心角所对的弧长是 .51. 若多项式2x2+3x-7的值为-10,则多项式6x2+9x+7的值为 .52. 若点(-1,y1)与(2,y2)在一次函数y=-2x+1的图象上,则y1y2(填>、<或=).53. 如图是正方体的表面展开图。则与“学”字相对的字是 .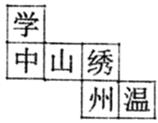 54. 命题“同旁内角互补”的逆命题是 .55. 三角形三边长分别为3,2a-1,4.则a的取值范围是 .56. 如图是七年级(1)班学生参加课外活动人数的扇形统计图,如果参加科普类的人数是10人,那么参加其它活动的人数是人.
54. 命题“同旁内角互补”的逆命题是 .55. 三角形三边长分别为3,2a-1,4.则a的取值范围是 .56. 如图是七年级(1)班学生参加课外活动人数的扇形统计图,如果参加科普类的人数是10人,那么参加其它活动的人数是人. 57. 如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED= °.
57. 如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED= °.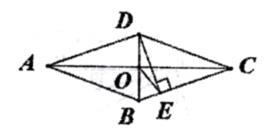 58. 在△ABC中,∠C=90°,AC=5,BC=12,则这个三角形外接圆的半径是 .59. 如图,正六边形ABCDEF的边长为1,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为 (结果保留根号和 ).
58. 在△ABC中,∠C=90°,AC=5,BC=12,则这个三角形外接圆的半径是 .59. 如图,正六边形ABCDEF的边长为1,以点A为圆心,AB的长为半径,作扇形ABF,则图中阴影部分的面积为 (结果保留根号和 ).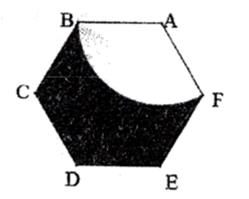 60. 如图,矩形ABCD的对角线AC,BD相交于点O,点M是CD的中点,连接OM并延长至E,使EM=OM,连接DE.CE.若AC=2,则四边形OCED的周长为 .
60. 如图,矩形ABCD的对角线AC,BD相交于点O,点M是CD的中点,连接OM并延长至E,使EM=OM,连接DE.CE.若AC=2,则四边形OCED的周长为 .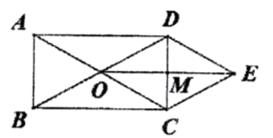 61. 甲、乙两人都加工a个零件,甲每小时加工20个,如果乙比甲晚工作1小时。且两人同时完成任务,那么乙每小时加工 个零件(用含a的代数式表示).62. 如图,一个可以自由转动的转盘,被分成了白色和红色两个区域,任意转动转盘两次,当转盘停止转动时(若指针停在边界处,则重新转动转盘),指针两次都落在白色区域内的概率是 .
61. 甲、乙两人都加工a个零件,甲每小时加工20个,如果乙比甲晚工作1小时。且两人同时完成任务,那么乙每小时加工 个零件(用含a的代数式表示).62. 如图,一个可以自由转动的转盘,被分成了白色和红色两个区域,任意转动转盘两次,当转盘停止转动时(若指针停在边界处,则重新转动转盘),指针两次都落在白色区域内的概率是 .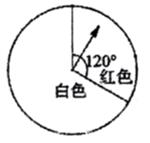 63. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与四边形BCEF的面积之比为 .
63. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与四边形BCEF的面积之比为 .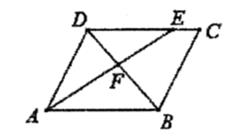 64. 如图,是一个运算程序的示意图,若开始输入x的值为24,第1次输出的结果为12,第2次输出的结果为6,……,则第2019次输出的结果为 。
64. 如图,是一个运算程序的示意图,若开始输入x的值为24,第1次输出的结果为12,第2次输出的结果为6,……,则第2019次输出的结果为 。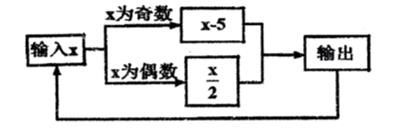 65. 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为1米,坡角∠A=30°,∠B=90°,BC=3米.当正方形DEFH运动到什么位置,即当AE= 米时,有DC2=AE2+BC2 .
65. 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为1米,坡角∠A=30°,∠B=90°,BC=3米.当正方形DEFH运动到什么位置,即当AE= 米时,有DC2=AE2+BC2 .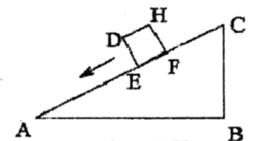 66. 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线,将图形分成面积相等的两部分.则将直线l向右平移3个单位后所得到直线l’的函数关系式为 .
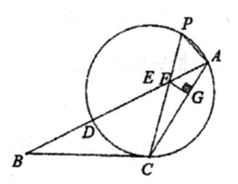
66. 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线,将图形分成面积相等的两部分.则将直线l向右平移3个单位后所得到直线l’的函数关系式为 . 67. 如图,四边形ABCD内接于⊙O,且AB是⊙O的直径,过点C的切线和过点D的切线交于点P.连接OP,若∠DAB=50°,∠CBA=70°,0A=6,则0P的长为 .
67. 如图,四边形ABCD内接于⊙O,且AB是⊙O的直径,过点C的切线和过点D的切线交于点P.连接OP,若∠DAB=50°,∠CBA=70°,0A=6,则0P的长为 .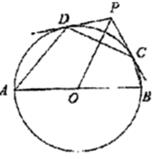 68. 如图,AB、AC是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的侧面积为15cm2 , 则sin∠BAC的值为 .
68. 如图,AB、AC是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的侧面积为15cm2 , 则sin∠BAC的值为 .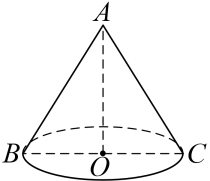 69. 如图,在等腰三角形纸片ABC中,AB=AC=4,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个直角三角形拼成一个平行四边形,并且这个平行四边形的一边长为4,则这个平行四边形较长的对角线的长是 .
69. 如图,在等腰三角形纸片ABC中,AB=AC=4,BC=6,沿底边BC上的高AD剪成两个三角形,用这两个直角三角形拼成一个平行四边形,并且这个平行四边形的一边长为4,则这个平行四边形较长的对角线的长是 .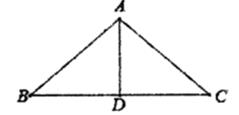 70. 如图,已知抛物线y=-x2+2x+3与X轴交于A,B两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,则P点到直线BC的距离PD的最大值是 .
70. 如图,已知抛物线y=-x2+2x+3与X轴交于A,B两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,则P点到直线BC的距离PD的最大值是 .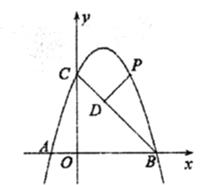 71. 如图,在正方形ABCD中,AB=5,点M在边CD上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到AABF,连接EF,则线段EF的长为 .
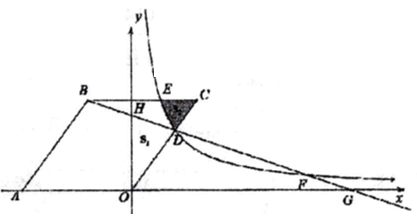
71. 如图,在正方形ABCD中,AB=5,点M在边CD上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到AABF,连接EF,则线段EF的长为 .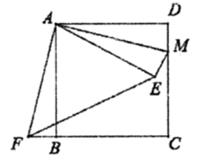 72. 某商户购进某种商品的进价是50元/个,根据市场调研发现售价是80元/个时,每月可卖出200个,若销售单价每降低1元,则每月可多卖出10个,同样若销售单价每增加1元,则每月可少卖出10个.若计划下月该商品的销售利润不低于5760元,则该商品的销售单价x(元)的取值范围是 .73. 如图,菱形OABC的顶点A的坐标是(-5,0),点B,C在x轴上方,反比例函数y= (k>0,x>0)的图象分别与边OC、BC交于点D、点E,射线BD交y轴子点H,交反比例函数图象于点F,交x轴于点G,BD:DF:FG=2:3:1,若记△ODH的面积为S1 , △CDE的面积为S2 , 则 的值是
72. 某商户购进某种商品的进价是50元/个,根据市场调研发现售价是80元/个时,每月可卖出200个,若销售单价每降低1元,则每月可多卖出10个,同样若销售单价每增加1元,则每月可少卖出10个.若计划下月该商品的销售利润不低于5760元,则该商品的销售单价x(元)的取值范围是 .73. 如图,菱形OABC的顶点A的坐标是(-5,0),点B,C在x轴上方,反比例函数y= (k>0,x>0)的图象分别与边OC、BC交于点D、点E,射线BD交y轴子点H,交反比例函数图象于点F,交x轴于点G,BD:DF:FG=2:3:1,若记△ODH的面积为S1 , △CDE的面积为S2 , 则 的值是