广东省珠海市2018-2019学年高三上学期文数期末考试试卷
试卷更新日期:2019-03-25 类型:期末考试
一、单选题
-
1. 复数 的共轭复数是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知集合 , ,则 ( )A、
2. 已知集合 , ,则 ( )A、 B、
B、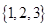 C、
C、 D、
D、 3. 函数 的图象大致为( )A、
3. 函数 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 4. 已知向量 =( ), =(-1,1),若 ,则 的值为( )A、 B、 C、1 D、25. 从2名男同学和3名女同学中任选2人参加社区服务,则选中一男一女同学的概率为( )A、
4. 已知向量 =( ), =(-1,1),若 ,则 的值为( )A、 B、 C、1 D、25. 从2名男同学和3名女同学中任选2人参加社区服务,则选中一男一女同学的概率为( )A、 B、0.6
C、
B、0.6
C、 D、
D、 6. 双曲线 的一条渐近线方程为 ,则双曲线的离心率为( )A、2 B、
6. 双曲线 的一条渐近线方程为 ,则双曲线的离心率为( )A、2 B、 C、
D、
C、
D、 7. 已知点 满足方程 ,则点 的轨迹为( )A、圆 B、椭圆 C、双曲线 D、抛物线8. 将函数 图象上所有的点的横坐标伸长到原来的2倍(纵坐标不变),再把图象向左平移 个单位长度,所得的图象关于 轴对称,则 ( )A、
7. 已知点 满足方程 ,则点 的轨迹为( )A、圆 B、椭圆 C、双曲线 D、抛物线8. 将函数 图象上所有的点的横坐标伸长到原来的2倍(纵坐标不变),再把图象向左平移 个单位长度,所得的图象关于 轴对称,则 ( )A、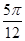 B、
B、 C、
C、 D、
9. 若 则 ( )A、
D、
9. 若 则 ( )A、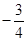 B、
C、
D、
B、
C、
D、 10. 在正方体 中,直线 与面 所成角的正弦为( )
10. 在正方体 中,直线 与面 所成角的正弦为( ) A、
A、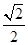 B、
C、
B、
C、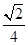 D、
11. 若 满足约束条件 ,目标函数 取得最大值时的最优解仅为 ,则 的取值范围为( )A、
D、
11. 若 满足约束条件 ,目标函数 取得最大值时的最优解仅为 ,则 的取值范围为( )A、 B、
B、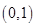 C、
C、 D、
D、 12. 有 ,且 时, ,则方程 的根有( )A、 个 B、 个 C、4 个 D、 个
12. 有 ,且 时, ,则方程 的根有( )A、 个 B、 个 C、4 个 D、 个二、填空题
-
13. 曲线f(x)= 的图象在点(0,f(0))处的切线斜率为2,则实数a的值为 .14. 某班级 四位学生 参加了文科综合知识竞赛,在竞赛结果公布前,地理老师预测得冠军的是 或 ;历史老师预测得冠军的是 ;政治老师预测得冠军的不可能是 或 ;语文老师预测得冠军的是 ,而班主任老师看了竞赛结果后说以上只有两位老师都说对了,则得冠军的是。15. 在 中, , , , 为 的中点,则 .16. 已知长方体 的棱长分别为3、4、5,一只蚂蚁由长方体的顶点 出发,沿长方体表面爬行到点 ,则蚂蚁爬行的最短路程长为 .

三、解答题
-
17. 已知 为等差数列 的前 项和,公差 ,且 成等比数列.(1)、求 , ;(2)、设 ,求 .18. 几何体 中,四边形 为直角梯形, , ,面 面 , ,三棱锥 的体积为 .
 (1)、求证: 面 ;(2)、求点 到面 的距离.19. 某花卉经销商销售某种鲜花,售价为每支5元,成本为每支2元.销售宗旨是当天进货当天销售.当天未售出的当垃圾处理.根据以往的销售情况,按 进行分组,得到如图所示的频率分布直方图.
(1)、求证: 面 ;(2)、求点 到面 的距离.19. 某花卉经销商销售某种鲜花,售价为每支5元,成本为每支2元.销售宗旨是当天进货当天销售.当天未售出的当垃圾处理.根据以往的销售情况,按 进行分组,得到如图所示的频率分布直方图. (1)、根据频率分布直方图计算该种鲜花日需求量的平均数 ,同一组中的数据用该组区间中点值代表;(2)、该经销商某天购进了400支这种鲜花,假设当天的需求量为x枝, ,利润为y元,求 关于 的函数关系式,并结合频率分布直方图估计利润 不小于800元的概率.20. 动圆P过点 ,且与直线 相切,设动圆圆心 的轨迹为曲线 .(1)、求曲线 的方程;(2)、过点F的直线交曲线C于A,B两个不同的点,过点A,B分别作曲线C的切线,且二者相交于点M,若直线 的斜率为 ,求直线 的方程.
(1)、根据频率分布直方图计算该种鲜花日需求量的平均数 ,同一组中的数据用该组区间中点值代表;(2)、该经销商某天购进了400支这种鲜花,假设当天的需求量为x枝, ,利润为y元,求 关于 的函数关系式,并结合频率分布直方图估计利润 不小于800元的概率.20. 动圆P过点 ,且与直线 相切,设动圆圆心 的轨迹为曲线 .(1)、求曲线 的方程;(2)、过点F的直线交曲线C于A,B两个不同的点,过点A,B分别作曲线C的切线,且二者相交于点M,若直线 的斜率为 ,求直线 的方程.