广东省肇庆市2018-2019学年高三上学期文数第二次(1月)统一检测试卷
试卷更新日期:2019-03-25 类型:高考模拟
一、单选题
-
1. 设集合 , ,则 ( )A、
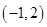 B、
B、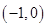 C、
C、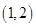 D、
D、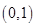 2. 若复数 满足 ,则 ( )A、
2. 若复数 满足 ,则 ( )A、 B、
C、
B、
C、 D、
3. 下列函数中,既是奇函数,又在其定义域上单调递增的是( )A、
D、
3. 下列函数中,既是奇函数,又在其定义域上单调递增的是( )A、 B、
B、 C、
C、 D、
D、 4. 若x,y满足约束条件 的取值范围是A、[0,6] B、[0,4] C、[6,
4. 若x,y满足约束条件 的取值范围是A、[0,6] B、[0,4] C、[6, D、[4,
D、[4,  5. 已知圆锥的底面半径是 ,且它的侧面展开图是半圆,则该圆锥的表面积是( )A、
5. 已知圆锥的底面半径是 ,且它的侧面展开图是半圆,则该圆锥的表面积是( )A、 B、
B、 C、
C、 D、
D、 6. 已知 的边 上有一点 满足 ,则 可表示为( )A、
6. 已知 的边 上有一点 满足 ,则 可表示为( )A、 B、
B、 C、
C、 D、
D、 7. 太极是中国古代的哲学术语,意为派生万物的本源.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼.太极图形象化地表达了阴阳轮转,相反相成是万物生成变化根源的哲理.太极图形展现了一种互相转化,相对统一的形式美.按照太极图的构图方法,在平面直角坐标系中,圆 被 的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为 ,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
7. 太极是中国古代的哲学术语,意为派生万物的本源.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼.太极图形象化地表达了阴阳轮转,相反相成是万物生成变化根源的哲理.太极图形展现了一种互相转化,相对统一的形式美.按照太极图的构图方法,在平面直角坐标系中,圆 被 的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为 ,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( ) A、
A、 B、
B、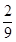 C、
C、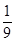 D、
D、 8. 已知双曲线 的中心为坐标原点,一条渐近线方程为 ,点 在 上,则 的方程为( )A、
8. 已知双曲线 的中心为坐标原点,一条渐近线方程为 ,点 在 上,则 的方程为( )A、 B、
B、 C、
C、 D、
D、 9. 由 的图象向左平移 个单位,再把所得图象上所有点的横坐标伸长到原来的 倍后, 所得图象对应的函数解析式为( )A、
9. 由 的图象向左平移 个单位,再把所得图象上所有点的横坐标伸长到原来的 倍后, 所得图象对应的函数解析式为( )A、 B、
B、 C、
C、 D、
D、 10. 在长方体 中, , 是 的中点,则三棱锥 外接球的表面积为( )A、
10. 在长方体 中, , 是 的中点,则三棱锥 外接球的表面积为( )A、 B、
B、 C、
C、 D、
D、 11. 已知 是 的极小值点,则实数 的取值范围是( )A、
11. 已知 是 的极小值点,则实数 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 12. 已知椭圆 的左右顶点分别为 , 是椭圆上异于 的一点,若直线 的斜率 与直线 的斜率 乘积 ,则椭圆 的离心率为( )A、 B、 C、 D、
12. 已知椭圆 的左右顶点分别为 , 是椭圆上异于 的一点,若直线 的斜率 与直线 的斜率 乘积 ,则椭圆 的离心率为( )A、 B、 C、 D、二、填空题
-
13. 某频率分布表(样本容量为 )不小心被损坏了一部分,只记得样本中数据在 内的频率为 ,则估计样本在 的数据个数之和是 .
分组
频数
14. 已知 ,则 .15. 已知 ,则 的值为 .16. 在平面凸四边形 中, ( 为常数),若满足上述条件的平面凸四边形 有且只有 个,则 的取值范围是 .三、解答题
-
17. 在数列 中,已知 .(1)、求证:数列 是等差数列;(2)、设数列 的前 和为 , ,求数列 的前 和 .18. 如图,在四棱锥 中,底面 是菱形, .
 (1)、证明: ;(2)、若面 面 , , , ,求 到平面 的距离.19. 已知椭圆 经过点 ,左焦点 ,直线 与椭圆 交于 两点, 是坐标原点.(1)、求椭圆 的标准方程;(2)、求 面积的最大值.20. 下图是某市 年至 年环境基础设施投资额 (单位:亿元)的条形图.
(1)、证明: ;(2)、若面 面 , , , ,求 到平面 的距离.19. 已知椭圆 经过点 ,左焦点 ,直线 与椭圆 交于 两点, 是坐标原点.(1)、求椭圆 的标准方程;(2)、求 面积的最大值.20. 下图是某市 年至 年环境基础设施投资额 (单位:亿元)的条形图. (1)、若从 年到 年的五年中,任意选取两年,则这两年的投资额的平均数不少于 亿元的概率;(2)、为了预测该市 年的环境基础设施投资额,建立了 与时间变量 的两个线性回归模型.根据 年至 年的数据(时间变量 的值依次为 )建立模型①: ;根据 年至 年的数据(时间变量 的值依次为 )建立模型②: .
(1)、若从 年到 年的五年中,任意选取两年,则这两年的投资额的平均数不少于 亿元的概率;(2)、为了预测该市 年的环境基础设施投资额,建立了 与时间变量 的两个线性回归模型.根据 年至 年的数据(时间变量 的值依次为 )建立模型①: ;根据 年至 年的数据(时间变量 的值依次为 )建立模型②: .(i)分别利用这两个模型,求该地区 年的环境基础设施投资额的预测值;
(ii)你认为用哪个模型得到的预测值更可靠?并说明理由.