广东省揭阳市2018-2019学年高中毕业班理数学业水平考试试卷
试卷更新日期:2019-03-25 类型:高考模拟
一、单选题
-
1. 复数 的虚部是( )A、
 B、2
C、
D、
B、2
C、
D、 2. 已知集合 , ,则 ( )A、
2. 已知集合 , ,则 ( )A、 B、
B、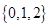 C、
C、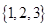 D、
D、 3. 已知命题 若 ,则 ;命题 、 是直线, 为平面,若 // , ,则 // .下列命题为真命题的是( )A、
3. 已知命题 若 ,则 ;命题 、 是直线, 为平面,若 // , ,则 // .下列命题为真命题的是( )A、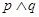 B、
B、 C、
C、 D、
D、 4. 如图是某地区2000年至2016年环境基础设施投资额 (单位:亿元)的折线图.则下列结论中表述不正确的是( )
4. 如图是某地区2000年至2016年环境基础设施投资额 (单位:亿元)的折线图.则下列结论中表述不正确的是( ) A、从2000年至2016年,该地区环境基础设施投资额逐年增加; B、2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多; C、2012年该地区基础设施的投资额比2004年的投资额翻了两番 ; D、为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为
A、从2000年至2016年,该地区环境基础设施投资额逐年增加; B、2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多; C、2012年该地区基础设施的投资额比2004年的投资额翻了两番 ; D、为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为 )建立了投资额y与时间变量t的线性回归模型
)建立了投资额y与时间变量t的线性回归模型  ,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
5. 函数 的图象大致为( )A、
,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.
5. 函数 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 6. 若 满足约束条件 ,则 的最小值为( )A、1 B、2 C、-2 D、-17. 若 , , ,则 的大小关系为( )A、
6. 若 满足约束条件 ,则 的最小值为( )A、1 B、2 C、-2 D、-17. 若 , , ,则 的大小关系为( )A、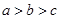 B、
B、 C、
C、 D、
D、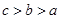 8. 若点 在抛物线 上,记抛物线 的焦点为 ,直线 与抛物线的另一交点为B,则 ( )A、
8. 若点 在抛物线 上,记抛物线 的焦点为 ,直线 与抛物线的另一交点为B,则 ( )A、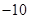 B、
B、 C、
C、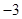 D、
D、 9. 某几何体示意图的三视图如图示,已知其主视图的周长为8,则该几何体侧面积的最大值为( )
9. 某几何体示意图的三视图如图示,已知其主视图的周长为8,则该几何体侧面积的最大值为( ) A、 B、
A、 B、 C、
D、
C、
D、 10. 已知在区间 上,函数 与函数 的图象交于点P,设点P在x轴上的射影为 , 的横坐标为 ,则 的值为( )
10. 已知在区间 上,函数 与函数 的图象交于点P,设点P在x轴上的射影为 , 的横坐标为 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、 11. 已知双曲线C: 的左、右焦点分别为 ,坐标原点O关于点 的对称点为P,点P到双曲线的渐近线距离为 ,过 的直线与双曲线C右支相交于M、N两点,若 , 的周长为10,则双曲线C的离心率为( )A、 B、2 C、
11. 已知双曲线C: 的左、右焦点分别为 ,坐标原点O关于点 的对称点为P,点P到双曲线的渐近线距离为 ,过 的直线与双曲线C右支相交于M、N两点,若 , 的周长为10,则双曲线C的离心率为( )A、 B、2 C、 D、3
12. 如图,在三棱柱 中, 底面 ,∠ACB=90°, 为 上的动点,则 的最小值为( )
D、3
12. 如图,在三棱柱 中, 底面 ,∠ACB=90°, 为 上的动点,则 的最小值为( ) A、 B、
A、 B、 C、5
D、
C、5
D、
二、填空题
-
13. 的展开式中 的系数为;14. 若向量 、 不共线,且 ,则 ;15. 已知函数 ,若 ,则实数 的取值范围是;16. 已知 ,则 .
三、解答题
-
17. 已知数列 的前n项和为 ,且满足 , .(1)、求数列 的通项公式;(2)、若等差数列 的前n项和为 ,且 , ,求数列 的前 项和 .18. 如图,在三棱锥P-ABC中,正三角形PAC所在平面与等腰三角形ABC所在平面互相垂直,AB=BC,O是AC中点,OH⊥PC于H.
 (1)、证明:PC⊥平面BOH;(2)、若 ,求二面角A-BH-O的余弦值.19. 某公司培训员工某项技能,培训有如下两种方式,方式一:周一到周五每天培训1小时,周日测试;方式二:周六一天培训4小时,周日测试.公司有多个班组,每个班组60人,现任选两组(记为甲组、乙组)先培训,甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如下表,其中第一、二周达标的员工评为优秀.
(1)、证明:PC⊥平面BOH;(2)、若 ,求二面角A-BH-O的余弦值.19. 某公司培训员工某项技能,培训有如下两种方式,方式一:周一到周五每天培训1小时,周日测试;方式二:周六一天培训4小时,周日测试.公司有多个班组,每个班组60人,现任选两组(记为甲组、乙组)先培训,甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如下表,其中第一、二周达标的员工评为优秀.第一周
第二周
第三周
第四周
甲组
20
25
10
5
乙组
8
16
20
16
(1)、在甲组内任选两人,求恰有一人优秀的概率;(2)、每个员工技能测试是否达标相互独立,以频率作为概率.(i)设公司员工在方式一、二下的受训时间分别为 、 ,求 、 的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
(ii)按(i)中所选方式从公司任选两人,求恰有一人优秀的概率.
20. 已知椭圆 : 的上顶点为A,以A为圆心,椭圆的长半轴为半径的圆与y轴的交点分别为 、 .(1)、求椭圆 的方程;(2)、设不经过点A的直线 与椭圆 交于P、Q两点,且 ,试探究直线 是否过定点?若过定点,求出该定点的坐标,若不过定点,请说明理由.