广东省惠州市2018-2019学年高二上学期理数期末考试试卷
试卷更新日期:2019-03-22 类型:期末考试
一、单选题
-
1. 命题“若 ,则 ”的否命题是( )A、若
 ,则
,则  B、若
B、若  ,则
,则  C、若
C、若  ,则
,则  D、若
D、若  ,则
,则  2. 若 是函数 的导函数,则 的值为( )A、1 B、3 C、1或3 D、43. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知向量 ,若 ,则实数 的值为( )A、
2. 若 是函数 的导函数,则 的值为( )A、1 B、3 C、1或3 D、43. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知向量 ,若 ,则实数 的值为( )A、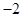 B、
B、 C、
C、 D、2
5. 执行如图所示的程序框图,若输入的 分别为1,2,3,则输出的 =( )
D、2
5. 执行如图所示的程序框图,若输入的 分别为1,2,3,则输出的 =( ) A、
A、 B、
B、 C、
C、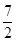 D、
D、 6. 某班有50名学生,男女人数不相等。随机询问了该班5名男生和5名女生的某次数学测试成绩,用茎叶图记录如下图所示,则下列说法一定正确的是( )
6. 某班有50名学生,男女人数不相等。随机询问了该班5名男生和5名女生的某次数学测试成绩,用茎叶图记录如下图所示,则下列说法一定正确的是( ) A、这5名男生成绩的标准差大于这5名女生成绩的标准差。 B、这5名男生成绩的中位数大于这5名女生成绩的中位数。 C、该班男生成绩的平均数大于该班女生成绩的平均数。 D、这种抽样方法是一种分层抽样。7. 已知 ,且 ,则 的最大值是( )A、 B、4 C、
A、这5名男生成绩的标准差大于这5名女生成绩的标准差。 B、这5名男生成绩的中位数大于这5名女生成绩的中位数。 C、该班男生成绩的平均数大于该班女生成绩的平均数。 D、这种抽样方法是一种分层抽样。7. 已知 ,且 ,则 的最大值是( )A、 B、4 C、 D、8
8. 抛掷2枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )A、
D、8
8. 抛掷2枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )A、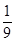 B、
B、 C、
C、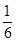 D、
D、 9. 设 满足约束条件 ,则 的最大值为( )A、
9. 设 满足约束条件 ,则 的最大值为( )A、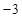 B、4
C、2
D、5
10. 点 是双曲线 上一点, 是双曲线的左,右焦点, ,则双曲线的离心率为( )A、 B、2 C、 D、11. 若正三棱柱 的所有棱长都相等,D是 的中点,则直线AD与平面 所成角的正弦值为( )A、 B、 C、 D、
B、4
C、2
D、5
10. 点 是双曲线 上一点, 是双曲线的左,右焦点, ,则双曲线的离心率为( )A、 B、2 C、 D、11. 若正三棱柱 的所有棱长都相等,D是 的中点,则直线AD与平面 所成角的正弦值为( )A、 B、 C、 D、 12. 已知 , ,使 成立,则 的取值范围是( )A、
12. 已知 , ,使 成立,则 的取值范围是( )A、 B、
B、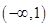 C、
C、 D、
D、
二、填空题
-
13. 利用计算机产生0~1之间的均匀随机数 ,则使关于 的一元二次方程 无实根的概率为 .14. 从编号为 的 件产品中,采用系统抽样的方法抽取容量为5的一组样本,若编号为 的产品在样本中,则该组样本中产品的最小编号为 .
15. 已知抛物线 的焦点为F,F关于原点的对称点为P,过F作 轴的垂线交抛物线于M,N两点,给出下列三个结论:① 必为直角三角形;
②直线 必与抛物线相切;
③ 的面积为 .其中正确的结论是 .
16. 已知点 ,圆C与直线MN切于点B,过M,N与圆C相切的两直线相交于点P,则P点的轨迹方程为 .三、解答题
-
17. 点 在抛物线 上,且A,B为 上两点,A与B的横坐标之和为4.(1)、求抛物线 的方程;(2)、求直线AB的斜率。18. 2019年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,按阅读时间分组:第一组[0,5), 第二组[5,10),第三组[10,15),第四组[15,20),第五组[20,25],绘制了频率分布直方图如下图所示。已知第三组的频数是第五组频数的3倍。
 (1)、求 的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;(2)、现从第三、四、五这3组中用分层抽样的方法抽取6人参加校“中华诗词比赛”。经过比赛后,从这6人中随机挑选2人组成该校代表队,求这2人来自不同组别的概率。19. 已知函数 .(1)、当 时,求函数 在点 处的切线方程;(2)、若 存在与直线 平行的切线,求 的取值范围。20. 某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
(1)、求 的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;(2)、现从第三、四、五这3组中用分层抽样的方法抽取6人参加校“中华诗词比赛”。经过比赛后,从这6人中随机挑选2人组成该校代表队,求这2人来自不同组别的概率。19. 已知函数 .(1)、当 时,求函数 在点 处的切线方程;(2)、若 存在与直线 平行的切线,求 的取值范围。20. 某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:年份
2011
2012
2013
2014
2015
2016
2017
年份代号
1
2
3
4
5
6
7
销售价格
3
3.4
3.7
4.5
4.9
5.3
6
附:参考公式: , ,其中 为样本平均值。
参考数据: .
(1)、求 关于x的线性回归方程;(2)、利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
