2018-2019学年初中数学人教版八年级下册 第十七章勾股定理 复习专练
试卷更新日期：2019-03-21 类型：单元试卷
一、选择题
-
1. 下列几组数中，不能作为直角三角形三边的是（ ）A、1， ， B、7，24，25 C、4，5，6 D、 ， ，12. 如图，在高为3米，斜坡长为5米的楼梯台阶上铺地毯，则地毯的长度至少要（ ）
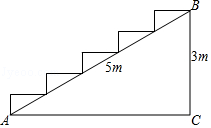A、4米 B、5米 C、6米 D、7米3. 如图，两个较大正方形的面积分别为225，289，则字母A所代表的正方形的面积为（ ）
A、4 B、8 C、16 D、644. 小明从一根长6m的钢条上截取一段后，截取的钢条恰好与两根长分别为3m、5m的钢条一起焊接成一个直角三角形钢架，则截取下来的钢条长应为（ ）A、4m B、
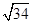m
C、4m或 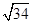m
D、6m
5. 如图所示，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（ ）
A、3 B、2 C、4 D、6. △ABC中，∠C＝90°，AC＝8cm，BC＝6cm．动点P从点C开始，按C→A→B→C的路径运动，速度为每秒2cm，运动的时间为t秒．以下结论中正确的有（ ）①t为6秒时，CP把△ABC的周长分成相等的两部分；
②t为6.5秒时，CP把△ABC的面积分成相等的两部分，且此时CP长为5cm；
③t为3秒或5.4秒或6秒或6.5秒时，△BCP为等腰三角形.
A、①②③ B、①② C、②③ D、①③7. 在Rt△ABC中，∠C＝90°，周长为24，斜边与一直角边之比为5：4，则这个直角三角形的面积是（ ）A、20 B、24 C、28 D、308. 如图，直角三角形三边上的等边三角形的面积从小到大依次记为S1、S2、S3 ， 则S1、S2、S3之间的关系是（ ）
A、S1+S2＞S3 B、S1+S2＜S3 C、S1+S2＝S3 D、S12+S22＞S329. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案．已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边（x＞y），下列四个说法：①x2+y2＝49；②x﹣y＝2；③x+y＝9；④2xy+4＝49；其中说法正确的是（ ）
A、①② B、①②③ C、①②④ D、①②③④10. 如图，在Rt△OBC中，OC＝1，OB＝2，数轴上点A所表示的数为a，则a的值是（ ）
A、﹣ ﹣2 B、﹣ C、 ﹣2 D、﹣ +211. 《九章算术》中记载：今有户不知高、广，竿不知长、短．横之不出四尺，从之不出二尺，斜之适出．问户高、广、斜各几何？译文是：今有门，不知其高、宽，有竿，不知其长、短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程为（ ）
A、x2＝（x﹣4）2+（x﹣2）2 B、2x2＝（x﹣4）2+（x﹣2）2 C、x2＝42+（x﹣2）2 D、x2＝（x﹣4）2+2212. 如图，东西方向上有A，C两地相距10千米，甲以16千米/时的速度从A地出发向正东方向前进，乙以12千米/时的速度从C地出发向正南方向前进，那么最快经过（ ）小时，甲、乙两人相距6千米？
A、 B、 C、1.5 D、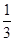
13. 如图，在△ABC中，∠C＝90°，O为△ABC的三条角平分线的交点，OD⊥BC，OE⊥AC，OF⊥AB，点D、E、F分别是垂足，且BC＝8cm，CA＝6cm，则点O到边AB的距离为（ ）
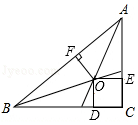A、2cm B、3cm C、4cm D、5cm14. 如图，有一个池塘，其底面是边长为10尺的正方形，一个芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′．则这根芦苇的长度是（ ）
A、10尺 B、11尺 C、12尺 D、13尺15. 如图，OA＝ ，以OA为直角边作Rt△OAA1 ， 使∠AOA1＝30°，再以OA1为直角边作Rt△OA1A2 ， 使∠A1OA2＝30°，……，依此法继续作下去，则A1A2的长为（ ）
A、
B、
C、
D、
二、填空题
-
16. 如图，在6×6正方形网格（每个小正方形的边长为1cm）中，网格线的交点称为格点，△ABC的顶点都在格点处，则AC边上的高的长度为cm．
17. 《九章算术》中记载“今有竹高一丈，末折抵地，去本三尺．问：折者高几何？”译文：一根竹子，原高一丈，虫伤有病，一阵风将竹子折断，其竹梢恰好着地，着地处离原竹子根部3尺远．问：原处还有多高的竹子？（1丈＝10尺）答：原处的竹子还有尺高．
18. 一种盛饮料的圆柱形杯，测得内部底面半径为2.5cm，高为12cm，吸管放进杯里（如图所示），杯口外面至少要露出3.6cm，为节省材料，管长acm的取值范围是 ．
19. 如图，△ABC中，∠A＝90°，AB＝3，AC＝6，点D是AC边的中点，点P是BC边上一点，若△BDP为等腰三角形，则线段BP的长度等于 ．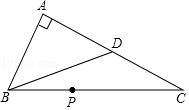
20. 如图，在Rt△ABC中，∠ACB＝90°，AB＝12cm，∠BAC＝60°，动点M从点B出发，在BA边上以每秒2cm的速度向点A匀速运动，同时动点N从C出发，在CB边上以每秒 cm的速度向B匀速运动，设运动时间为t秒（0＜t＜6），连接MN，若△BMN是等腰三角形，则t的值为 ．
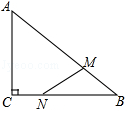21. 如图，在Rt△ABC中，∠C＝90°，BC＝6，∠ABC的平分线BD交AC于D，且BD＝10，点E是AB边上的一动点，则DE的最小值为 ．
22. 如图，在四边形ABCD中，∠ADC＝∠ABC＝45°，CD＝ ，BC＝ ，连接AC、BD，若AC⊥AB，则BD的长度为 ．
23. 《九章算术》卷九“勾股”中记载：今有立木，系索其末，委地三尺．引索却行，去本八尺而索尽，问索长几何？译文：今有一竖立着的木柱，在木柱的上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有3尺．牵着绳索（绳索头与地面接触）退行，在距木根部8尺处时绳索用尽．问绳索长是多少？设绳索长为x尺，可列方程为 ．24. 已知：如图，四边形ABDC，AB＝4，AC＝3，CD＝12，BD＝13，∠BAC＝90°．则四边形ABDC的面积是 ．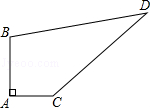
25. 如图，Rt△ABC中，∠B＝90°，AB＝8cm，BC＝6cm，D点从A出发以每秒1cm的速度向B点运动，当D点运动到AC的中垂线上时，运动时间为秒．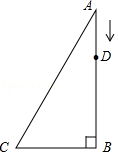
三、解答题
-
26. 如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝BC＝2，CD＝1，求AD的长．
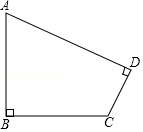
27. 图1是围墙的一部分，上部分是由不锈钢管焊成的等腰三角形栅栏如图2，请你根据图2所标注的尺寸，求焊成一个等腰三角形栅栏外框BCD至少需要不锈钢管多少米（焊接部分忽略不计）．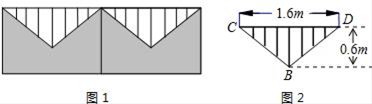
28. 如图1，Rt△ABCAC⊥CB，AC＝15，AB＝25，点D为斜边上动点．
(1)、如图2，过点D作DE⊥AB交CB于点E，连接AE，当AE平分∠CAB时，求CE；
(2)、如图3，在点D的运动过程中，连接CD，若△ACD为等腰三角形，求AD．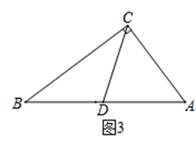
29. 如图，△ABC中，∠ACB＝90°，AB＝10cm，BC＝6cm，若点P从点A出发，以每秒1cm的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）．
(1)、当点P在AC上，且满足PA＝PB时，求出此时t的值；(2)、当点P在AB上，求出t为何值时，△BCP为等腰三角形．30. 如图，有两根长杆隔河相对，一杆高3m，另一杆高2m，两杆相距5m．两根长杆都与地面垂直，现两杆顶部各有一只鱼鹰，它们同时看到两杆之间的河面上E处浮出一条小鱼，于是同时以同样的速度飞下来夺鱼，结果两只鱼鹰同时叼住小鱼．求两杆底部距小鱼的距离各是多少米．（假设小鱼在此过程中保持不动）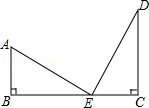
31.
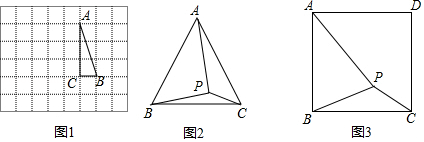
如图（1）：已知在△ABC中，AB＝AC，P是底边BC上一点，作PD⊥AB于D，PE⊥AC于E，BF⊥AC于F，求证：PD+PE＝BF．
【思路梳理】：如图（2）：连接AP，必有S△APB+S△APC＝S△ABC ， 因为△ABP、△ACP和△ABC的底相等，所以三条高PD、PE和BF满足关系：PD+PE＝BF．
(1)、【变式应用】：如图（3）：已知在△ABC中，AB＝AC，P是底边BC的反向延长线上一点，作PD⊥AB于D，PE⊥AC于E，BF⊥AC于F，求证：PE﹣PD＝BF．(2)、【类比引申】：如图（4）：已知P是边长为4cm等边△ABC内部一点，作PD⊥BC于D，PE⊥AB于E，PF⊥AC于F，那么PD+PE+PF＝ ．(3)、【联想拓展】：已知某三角形的三条边分别是5cm、12cm、13cm，在平面上有一点P，它到此三角形的三边的距离相等，则这个距离等于 ．32. 学完勾股定理之后，同学们想利用升旗的绳子、卷尺，测算出学校旗杆的高度．爱动脑筋的小明这样设计了一个方案：如图，小亮将升旗的绳子拉直到末端刚好接触地面，测得此时绳子末端距旗杆底端1米，然后将绳子末端拉直到距离旗杆5m处，测得此时绳子末端距离地面高度为1m，如果设旗杆的高度为x米（滑轮上方的部分忽略不计），求x的值．
33. 已知：如图，在Rt△ABC中，∠ACB＝90°，AB＝5cm，AC＝3cm，动点P从点B出发沿射线BC以2cm/s的速度运动，设运动的时间为t秒，
(1)、当△ABP为直角三角形时，求t的值：(2)、当△ABP为等腰三角形时，求t的值．（本题可根据需要，自己画图并解答）
34. 如图1中A村和B村在一条大河CD的同侧，它们到河岸的距离AC、BD分别为1千米和4千米，又知道CD的长为4千米．
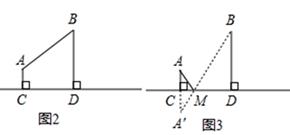(1)、现要在河岸CD上建一水厂向两村输送自来水．有两种方案备选．方案1：水厂建在C点，修自来水管道到A村，再到B村（即AC+AB）．（如图2）
方案2：作A点关于直线CD的对称点A′，连接A′B交CD于M点，水厂建在M点处，分别向两村修管道AM和BM．（即AM+BM）（如图3）
从节约建设资金方面考虑，将选择管道总长度较短的方案进行施工．请利用已有条件分别进行计算，判断哪种方案更合适．
(2)、有一艘快艇Q从这条河中驶过，当快艇Q与CD中点G相距多远时，△ABQ为等腰三角形？直接写出答案，不要说明理由．35. 今年最强台风“山竹”9月13日在我国登陆，A市于上午8：00接到台风警报时，台风中心位于A市正南方向125km的B处，正以20km/h的速度沿BC方向移动．已知A市到BC的距离AD＝35km，在距离台风中心45km的区域内（包括45km）都将受到台风的影响．试问：A市何时受到台风影响，受到台风的影响的时间是多长？（ ≈1.4）
36.
(1)、（操作发现）如图1，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．请接要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′，则∠AB′B＝ ．
(2)、（问题解决）如图2，在等边三角形ABC内有一点P，且PA＝2，PB＝ ，PC＝1，求∠BPC的度数和等边三角形ABC的边长；
(3)、（灵活运用）如图3，在正方形ABCD内有一点P，且PA＝ ，BP＝ ，PC＝1，求∠BPC的度数．
37. 如图，正方形网格中有△ABC．若每个小方格边长均为1，请你根据所学的知识解答下列问题：
(1)、判断△ABC的形状，并说明理由；(2)、求△ABC中BC边上的高．38. 小明和同桌小聪在课后复习时，对练习册“目标与评定”中的一道思考题，进行了认真地探索．（思考题）如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？
(1)、请你将小明对“思考题”的解答补充完整：解：设点B将向外移动x米，即BB1＝x，
则A1B1＝2.5，在Rt△A1B1C中，由B1C2+A1C2＝A1B12 ，
得方程 ， 解方程，得x1＝ ， x2＝ ， ∴点B将向外移动米．
(2)、解完“思考题”后，小聪提出了如下两个问题：（问题一）在“思考题”中，将“下滑0.4米”改为“下滑0.9米”，那么该题的答案会是0.9米吗？为什么？
（问题二）在“思考题”中，梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？为什么？
请你解答小聪提出的这两个问题．
39. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．
(1)、问CH是否为从村庄C到河边的最近路？（即问：CH与AB是否垂直？）请通过计算加以说明；(2)、求原来的路线AC的长．40. 已知，如图，在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝18cm．动点P从点A出发，沿AB向点B运动，动点Q从点B出发，沿BC向点C运动，如果动点P以2cm/s，Q以1cm/s的速度同时出发，设运动时间为t（s），解答下列问题：
(1)、t为时，△PBQ是等边三角形？(2)、P，Q在运动过程中，△PBQ的形状不断发生变化，当t为何值时，△PBQ是直角三角形？说明理由．