数学(苏科版)八年级下册第7章 7.2统计表、统计图的选用 同步练习
试卷更新日期:2017-04-28 类型:同步测试
一、单选题
-
1. 空气是由多种气体混合而成,为了简明扼要地说明空气的组成情况,使用的统计图最好是( )A、扇形统计图 B、条形统计图 C、折线统计图 D、频数分布直方图2. 江都区三月份第一周连续七天的空气质量指数(AQI)分别为:118,96,60,82,56,69,86.则这七天空气质量变化情况最适合用哪种统计图描述( )A、扇形统计图 B、条形统计图 C、折线统计图 D、以上都不对3. 能反映事物发展变化的规律和趋势的统计图是( )
A、条形统计图 B、扇形统计图 C、折线统计图 D、环形统计图4. 能清楚的看出每个项目的具体数量的统计图是( )A、扇形统计图 B、折线统计图 C、条形统计图 D、以上三种均可5. 要清楚地表示出个部分在总体积中所占的百分比,应选择( )A、条形统计图 B、折线统计图 C、扇形统计图 D、上述3种都可以6. 要反映嘉兴市一天内气温的变化情况宜采用( )A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布直方图7. 为了直观地表示世界七大洲的面积各占全球陆地面积的百分比,最适合使用的统计图是( )A、扇形图 B、条形图 C、折线图 D、直方图8. 记录一个人的体温变化情况,最好选用( )A、条形统计图 B、折线统计图 C、扇形统计图 D、统计表9. 下列说法中不正确的是( )A、要反映我市一周内每天的最低气温的变化情况宜采用折线统计图 B、打开收音机正在播放TFBOYS的歌曲是必然事件 C、方差反映了一组数据的稳定程度 D、为了解一种灯泡的使用寿命.应采用抽样调查的办法10. 能清楚地表示出各部分在总体中所占百分比的统计图是( )A、条形统计图 B、扇形统计图 C、折线统计图 D、都可以11. 为了参加市中学生篮球运动会,一支校篮球队准备购买双运动鞋,各种尺码的统计如表所示,则这双运动鞋尺码的众数和中位数分别为( )尺码(厘米)
25
25.5
26
26.5
27
购买量(双)
1
4
2
1
1
A、25.5cm 26 cm B、26 cm 25.5 cm C、25.5 cm 25.5 cm D、26 cm 26 cm12. 空气是由多种气体混合而成的,为了简明扼要的介绍空气的组成情况,较好的描述数据,最适合使用的统计图是( )A、扇形图 B、条形图 C、折线图 D、直方图二、填空题
-
13. 要反映一感冒病人一天的体温的变化情况,宜采用统计图.
14. 空气是由多种气体混合而成的,为了简明扼要的介绍空气的组成情况,较好的描述数据,最适合使用的统计图是 .15. 某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.16. 王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是人.组 别
A型
B型
AB型
O型
频 率
x
0.4
0.15
0.1
17. 常用统计图的类型有:、、 .三、解答题
-
18. 阅读下列材料:
数学课程内容分为“数与代数”、“图形与几何”、“统计与概率”、“综合与实践”四个领域,其中“综合与实践”领域通过探讨一些具有挑战性的研究问题,给我们创造了可以动手操作、探究学习、认识数学知识间的联系、发展应用数学知识解决问题的意识和能力的机会.“综合与实践”领域在人教版七﹣九年级6册数学教材中共安排了约40课时的内容,主要有“数学制作与设计”、“数学探究与实验”、“数学调查与测量”、“数学建模”等活动类型,所占比例大约为30%,20%,40%,10%.这些活动以“课题学习”、“数学活动”和“拓广探索类习题”等形式分散于各章之中.“数学活动”几乎每章后都有2~3个,共60个,其中七年级22个,八年级19个;“课题学习”共7个,其中只有八年级下册安排了“选择方案”和“体质健康测试中的数据分析”2个内容,其他5册书中都各有1个;七上﹣九下共6册书中“拓广探索类习题”数量分别为44,39,46,35,37,23.
根据以上材料回答下列问题:
(1)人教版七﹣九年级数学教材中,“数学调查与测量”类活动约占多少课时;
(2)选择统计表或统计图,将人教版七﹣九年级数学教材中“课题学习”、“数学活动”和“拓广探索类习题”的数量表示出来.
四、综合题
-
19. 为了让同学们了解自己的体育水平,初二1班的体育康老师对全班45名学生进行了一次体育模拟测试(得分均为整数)成绩满分为10分,成绩达到9分以上(包含9分)为优秀,成绩达到6分以上(包含6分)为合格,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
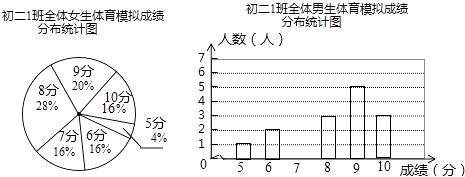
初二1班体育模拟测试成绩分析表
平均分
方差
中位数
众数
合格率
优秀率
男生
2
8
7
95%
40%
女生
7.92
1.99
8
96%
36%
根据以上信息,解答下列问题:
(1)、在这次测试中,该班女生得10分的人数为4人,则这个班共有女生人;(2)、补全初二1班男生体育模拟测试成绩统计图,并把相应的数据标注在统计图上;(3)、补全初二1班体育模拟测试成绩分析表;(4)、你认为在这次体育测试中,1班的男生队、女生队哪个表现更突出一些?并写出一条支持你的看法的理由;(5)、体育康老师说,从整体看,1班的体育成绩在合格率方面基本达标,但在优秀率方面还不够理想,因此他希望全班同学继续加强体育锻炼,争取在期末考试中,全班的优秀率达到60%,若男生优秀人数再增加6人,则女生优秀人数再增加多少人才能完成康老师提出的目标?20. 在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
(1)、按表格数据格式,表中的a=;b=;(2)、请估计:当次数s很大时,摸到白球的频率将会接近;(3)、请推算:摸到红球的概率是(精确到0.1);(4)、试估算:口袋中红球有多少只?(5)、解决了上面4个问题后,请你从统计与概率方面谈一条启示.21. 6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图.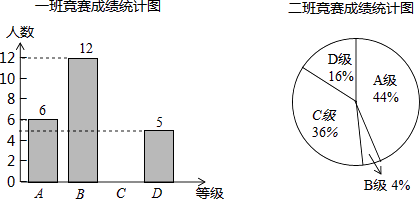
平均数(分)
中位数(分)
众数(分)
一班
a
b
90
二班
d
80
c
(1)、把一班竞赛成绩统计图补充完整;(2)、写出表中a、b、c的值:平均数(分)
中位数(分)
众数(分)
一班
a
b
90
二班
d
80
c
(3)、请从平均数和中位数方面比较一班和二班的成绩,对这次竞赛成绩的结果进行分析.22. 某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)1号
2号
3号
4号
5号
总分
甲班
89
100
96
118
97
500
乙班
100
95
110
91
104
500
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题:
(1)、计算两班的优秀率;(2)、求两班比赛数据的中位数;(3)、计算两班比赛数据的方差;(4)、你认为应该定哪一个班为冠军?为什么?
-