贵州省部分重点中学2018-2019学年高三理数3月联考试卷

试卷更新日期：2019-03-21 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x + 1 \geq 0}$ ， $B = {x | x^{2} + 3 x < 0}$ ，则 $A \cap^{} B =$ （）

A、 B、 C、 D、

查看试题解析
2. 已知 $\frac{a + i}{i} = b + i (a, b \in R)$ ，则 $a + b =$ （）

A、-2 B、0 C、1 D、2

查看试题解析
3. 若双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的离心率为 $\sqrt{5}$ ，则斜率为正的渐近线的斜率为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{1}{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
4. 自古以来“民以食为天”，餐饮业作为我国第三产业中的一个支柱产业，一直在社会发展与人民生活中发挥着重要作用.某机构统计了2010～2016年餐饮收入的情况，得到下面的条形图，则下面结论中不正确的是（）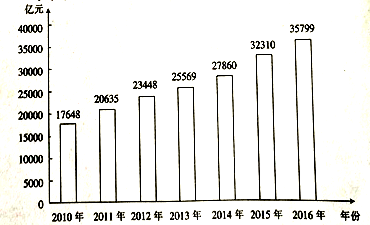

A、2010～2016年全国餐饮收入逐年增加 B、2016年全国餐饮收入比2010年翻了一番以上 C、2010～2016年全国餐饮收入同比增量最多的是2015年 D、2010～2016年全国餐饮收入同比增量超过3000亿元的年份有3个

查看试题解析
5. 函数 $f (x) = cos x + cos (x - \frac{π}{3})$ 的一个单调递增区间为（）

A、 B、 C、 D、

查看试题解析
6. 设 $x ， y$ 满足约束条件 ${\begin{matrix} x + 2 y \geq 0 \\ x - y \leq 0 \\ y - 4 \leq 0 \end{matrix}$ ，则 $z = x + y$ 的最大值是（）

A、-4 B、0 C、8 D、12

查看试题解析
7. 已知 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和，已知 $a_{3} + S_{5} = 18$ ， $a_{5} = 7$ .若 $a_{3}$ ， $a_{6}$ ， $a_{m}$ 成等比数列，则 $m =$ （）

A、15 B、17 C、19 D、21

查看试题解析
8. 某几何体的三视图如图所示，则该几何体的表面积为（）

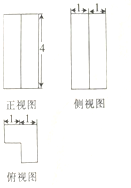A、32 B、34 C、36 D、38

查看试题解析
9. 下面的程序框图是为了求出满足 $1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{i} > 2 (i \in N^{*})$ 的最小偶数，那么在“ □”和“ 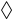”两个空白框中，可以分别填入（）

A、和是奇数 B、和是奇数 C、和是偶数 D、和是偶数

查看试题解析
10. 已知函数 $f (x) = {\begin{matrix} 2 x + 1 ， x \leq 1 \\ l n x + 1 ， x > 1 \end{matrix}$ ，则满足 $f (x) + f (x + 1) > 1$ 的 $x$ 的取值范围是（）

A、 B、 C、 $(0, + \infty)$ D、

查看试题解析
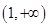11. 在直角坐标系 $x O y$ 中，抛物线 $M$ ： $y^{2} = 2 p x (p > 0)$ 与圆 $C$ ： $x^{2} + y^{2} - 2 \sqrt{3} y = 0$ 相交于两点，且两点间的距离为 $\sqrt{6}$ ，则抛物线 $M$ 的焦点到其准线的距离为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ C、 D、 $\sqrt{6}$

查看试题解析
12. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形，侧棱 $A P ⊥$ 平面 $A B C D$ ， $A B = 1$ ， $A P = \sqrt{3}$ ，点 $M$ 在线段 $B C$ 上，且 $A M ⊥ M D$ ，则当 $Δ P M D$ 的面积最小时，线段 $B C$ 的长度为（）

A、 $\sqrt{3}$ B、 C、2 D、

查看试题解析

二、填空题

13. 设等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $a_{1} - a_{2} = 2$ ， $a_{2} - a_{3} = 6$ ，则 $S_{4} =$ ．

查看试题解析
14. 在 $Δ A B C$ 中， $C = 90 °$ ，点 $D$ 在 $A B$ 上， $\overset{⇀}{A D} = 3 \overset{⇀}{D B}$ ， $| \overset{⇀}{C B} | = 4$ ，则 $\overset{⇀}{C B} \cdot \overset{⇀}{C D} =$ ．

查看试题解析
15. 把 $A$ ， $B$ ， $C$ ， $D$ 四本不同的书分给三位同学，每人至少分到一本，每本书都必须有人分到， $A$ ， $B$ 不能同时分给同一个人，则不同的分配方式共有种（用数字作答）．

查看试题解析
16. 设 $m$ ， $n \in R$ ，那么 ${(m - e^{n})}^{2} + {(n - e^{m})}^{2}$ 的最小值是．

查看试题解析

三、解答题

17. 在 $Δ A B C$ 中，内角 $A, B, C$ 的对边分别为 $a, b, c$ ，已知 $(sin A + sin B) (a - b) = (sin C - sin B) c$ .

(1)、求 $A$ ；

(2)、已知 $a = 2$ ， $Δ A B C$ 的面积为 $\frac{\sqrt{3}}{2}$ ，求 $Δ A B C$ 的周长.

查看试题解析
18. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C = B C = 1$ ， $A B = \sqrt{2}$ ， $B_{1} C = 1$ ， $B_{1} C ⊥$ 平面 $A B C$ .

(1)、证明： $A C ⊥$ 平面 $B C C_{1} B_{1}$ ；

(2)、求二面角 $A_{1} - A C - B$ 的大小.

查看试题解析
19. 已知甲、乙两名工人在同样条件下每天各生产100件产品，且每生产1件正品可获利20元，生产1件次品损失30元，甲，乙两名工人100天中出现次品件数的情况如表所示.

甲每天生产的次品数/件

0

1

2

3

4

对应的天数/天

40

20

20

10

10

乙每天生产的次品数/件

0

1

2

3

对应的天数/天

30

25

25

20

(1)、将甲每天生产的次品数记为 $x$ （单位：件），日利润记为 $y$ （单位：元），写出 $y$ 与 $x$ 的函数关系式；

(2)、如果将统计的100天中产生次品量的频率作为概率，记 $X$ 表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和，求随机变量 $X$ 的分布列和数学期望.

查看试题解析
20. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为 $F$ ，上顶点为 $M$ ，直线 $F M$ 的斜率为 $- \frac{\sqrt{2}}{2}$ ，且原点到直线 $F M$ 的距离为 $\frac{\sqrt{6}}{3}$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、若不经过点 $F$ 的直线 $l$ ： $y = k x + m (k 〈 0, m 〉 0)$ 与椭圆 $C$ 交于 $A, B$ 两点，且与圆 $x^{2} + y^{2} = 1$ 相切.试探究 $Δ A B F$ 的周长是否为定值，若是，求出定值；若不是，请说明理由.

查看试题解析
21. 已知函数 $f (x) = e^{2 x} + a e^{x} - a^{2} x$ .

(1)、当 $a = 2$ 时，求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

(2)、当 $a \geq 0$ 时，讨论函数 $f (x)$ 的零点个数.

查看试题解析
22. 在直角坐标系 $x O y$ 中，直线 $l$ 的方程为 $k x - y + 2 k = 0$ ，曲线 $C_{1}$ ： ${\begin{matrix} x = c o s φ, \\ y = s i n φ \end{matrix}$ （ $φ$ 为参数， $0 \leq φ \leq π$ ），在以原点 $O$ 为极点， $x$ 轴正半轴为极轴的极坐标系中，曲线 $C_{2}$ ： $ρ (sin θ + cos θ) - 1 = 0$ .

(1)、求曲线 $C_{1}$ 的普通方程和曲线 $C_{2}$ 的直角坐标方程；

(2)、若直线 $l$ 与曲线 $C_{1}$ 有公共点，且直线 $l$ 与曲线 $C_{2}$ 的交点 $P$ 恰好在曲线 $C_{1}$ 与 $x$ 轴围成的区域（不含边界）内，求 $k$ 的取值范围.

查看试题解析
23. 已知函数 $f (x) = | x - a | - 2 x - 1$ .

(1)、当 $a = - 2$ ，解不等式 $f (x) \leq 0$ ；

(2)、当 $a = 1$ 时，若存在 $x \in R$ 使不等式 $f (x) + | x + 2 | \leq m$ 成立，求 $m$ 的取值范围.

查看试题解析

甲每天生产的次品数/件	0	1	2	3	4
对应的天数/天	40	20	20	10	10

乙每天生产的次品数/件	0	1	2	3
对应的天数/天	30	25	25	20