安徽省江淮十校2018-2019学年高三上学期文数第一次联考试卷
试卷更新日期:2019-03-21 类型:高考模拟
一、单选题
-
1. 已知集合 ,集合 0,1,3, ,则A、
 1,
1,  B、
B、 C、
C、 0,1,
0,1,  D、
D、 1,
1,  2. 若复数 i为虚数单位 是纯虚数,则实数a的值为A、0 B、
2. 若复数 i为虚数单位 是纯虚数,则实数a的值为A、0 B、 C、
C、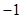 D、1
3. 为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图 如图所示 ,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是
D、1
3. 为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为200的调查样本,其中城镇户籍与农村户籍各100人;男性120人,女性80人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图 如图所示 ,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是 A、是否倾向选择生育二胎与户籍有关 B、是否倾向选择生育二胎与性别有关 C、倾向选择生育二胎的人群中,男性人数与女性人数相同 D、倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数4. 若公比为2的等比数列 的前n项和为 ,且 ,9, 成等差数列,则A、
A、是否倾向选择生育二胎与户籍有关 B、是否倾向选择生育二胎与性别有关 C、倾向选择生育二胎的人群中,男性人数与女性人数相同 D、倾向选择不生育二胎的人群中,农村户籍人数少于城镇户籍人数4. 若公比为2的等比数列 的前n项和为 ,且 ,9, 成等差数列,则A、 B、
B、 C、
C、 D、
D、 5. 已知函数 是定义在R上的偶函数,且在 上单调递增,则A、
5. 已知函数 是定义在R上的偶函数,且在 上单调递增,则A、 B、
B、 C、
C、 D、
D、 6. 已知实数x , y满足 ,则 的最大值是A、2 B、3 C、4 D、57. 用24个棱长为1的小正方体组成 的长方体,将共顶点的某三个面涂成红色,然后将长方体拆散开,搅拌均匀后从中任取一个小正方体,则它的涂成红色的面数为1的概率为A、
6. 已知实数x , y满足 ,则 的最大值是A、2 B、3 C、4 D、57. 用24个棱长为1的小正方体组成 的长方体,将共顶点的某三个面涂成红色,然后将长方体拆散开,搅拌均匀后从中任取一个小正方体,则它的涂成红色的面数为1的概率为A、 B、
B、 C、
C、 D、
8. 执行如图所示的程序框图,则输出的结果是
D、
8. 执行如图所示的程序框图,则输出的结果是 A、225 B、75 C、275 D、3009. 将函数 图象上所有点向左平移 个单位,再将横坐标伸长为原来的2倍 纵坐标不变 ,得到 的图象,则下列叙述正确的是A、
A、225 B、75 C、275 D、3009. 将函数 图象上所有点向左平移 个单位,再将横坐标伸长为原来的2倍 纵坐标不变 ,得到 的图象,则下列叙述正确的是A、 是
是  的对称轴
B、
的对称轴
B、 是
是  的对称中心
C、
的对称中心
C、 D、
D、 10. 一个几何体的三视图如图所示,则这个几何体的体积为
10. 一个几何体的三视图如图所示,则这个几何体的体积为 A、
A、 B、
B、 C、
C、 D、
D、 11. 若对 , ,且 ,都有 ,则m的最小值是 注: 为自然对数的底数,即A、
11. 若对 , ,且 ,都有 ,则m的最小值是 注: 为自然对数的底数,即A、 B、e
C、1
D、
B、e
C、1
D、
二、填空题
-
12. 若 ,则 .13. 已知平面向量 , ,且 ,则14. 若圆C: ,关于直线 对称,则由点 向圆所作的切线长的最小值为 .15. 如图所示,点A , B , C在以点O为球心的球面上,已知 , , ,且点O到三角形ABC所在平面的距离为 ,则该球的表面积为

三、解答题
-
16. 设数列 的前n和为 ,已知 , , .(1)、求数列 的通项公式;(2)、求数列 的前n和 .17. 在 中,a , b , c分别为内角A , B , C的对边,且 .(1)、求角C的大小;(2)、若 , ,求 的面积.18. 下表为2014年至2017年某百货零售企业的线下销售额 单位:万元 ,其中年份代码 年份 .
年份代码x
1
2
3
4
线下销售额y
95
165
230
310
(1)、已知y与x具有线性相关关系,求y关于x的线性回归方程,并预测2018年该百货零售企业的线下销售额;(2)、随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调査平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了55位男顾客、50位女顾客 每位顾客从“持乐观态度”和“持不乐观态度”中任选一种 ,其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有10人、女顾客有20人,能否在犯错误的概率不超过 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?参考公式及数据: , , ,
19. 已知直角梯形ABCD中, , , , , ,如图1所示,将 沿BD折起到 的位置,如图2所示.
1 当平面 平面PBC时,求三棱锥 的体积;