浙江省瑞安市联考2016-2017学年下九年级第一次学业调研数学试题
试卷更新日期:2017-04-27 类型:中考模拟
一、选择题
-
1. 给出四个数0, ,- ,0.3,其中属于无理数的是( )A、0 B、 C、- D、0.32.
如图是一个立方体挖去一个小立方体后的示意图,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 不等式组 的解集是( )A、-2≤x<1 B、x≥-2 C、x>1 D、-1≤x<24. 已知抛物线 的开口向下,顶点坐标为(2,-3),那么该二次函数有( )A、最小值-3 B、最大值-3 C、最小值2 D、最大值25. 某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
3. 不等式组 的解集是( )A、-2≤x<1 B、x≥-2 C、x>1 D、-1≤x<24. 已知抛物线 的开口向下,顶点坐标为(2,-3),那么该二次函数有( )A、最小值-3 B、最大值-3 C、最小值2 D、最大值25. 某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):成绩(分)
14
15
16
17
18
19
20
人数(人)
1
3
2
2
1
2
2
这13名学生听力测试成绩的中位数是( )
A、16分 B、17分 C、18分 D、19分6. 如图,在△ABC中,∠C=90°,BC=5,AB=13,则sinB是( ) A、 B、 C、 D、7. P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知 、 的度数别为88°、32°,则∠P的度数为( )
A、 B、 C、 D、7. P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知 、 的度数别为88°、32°,则∠P的度数为( ) A、26° B、28° C、30° D、32°8. 要使关于x的方程x2﹣2x+3k=0有两个不相等的实数根,则下列k的取值正确的是( )A、1 B、2 C、 D、9. 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
A、26° B、28° C、30° D、32°8. 要使关于x的方程x2﹣2x+3k=0有两个不相等的实数根,则下列k的取值正确的是( )A、1 B、2 C、 D、9. 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )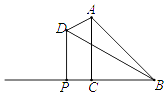 A、一直变大 B、一直变小 C、先变小再变大 D、先变大再变小10. 如图,反比例函数 的图象与边长为5的等边△AOB的边OA , AB分别相交于C , D两点,若OC=2BD , 则实数k的值为( )
A、一直变大 B、一直变小 C、先变小再变大 D、先变大再变小10. 如图,反比例函数 的图象与边长为5的等边△AOB的边OA , AB分别相交于C , D两点,若OC=2BD , 则实数k的值为( )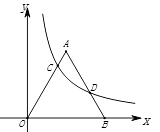 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: = .12. 一次函数 的图象与x轴的交点坐标为 .13.
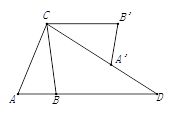
如图,将△ABC绕点C按逆时针方向旋转得到△A′B′C′,且AB//B′C′,分别延长AB、CA′相交于点D , 若∠A=70°,∠D=30°,则∠BCD的度数为 .
 14. 如图,正方形ABCD中,P , Q是BC边上的三等分点,连接AQ、DP交于点R . 若正方形ABCD的面积为144cm2 , 则△PQ R的面积为cm2 .
14. 如图,正方形ABCD中,P , Q是BC边上的三等分点,连接AQ、DP交于点R . 若正方形ABCD的面积为144cm2 , 则△PQ R的面积为cm2 . 15. 在“校园文化”建设中,某校用8 000元购进一批绿色植物,种植在礼堂前的空地处.根据建设方案的要求,该校又用7500元购进第二批绿植植物.若两次所买植物的盆数相同,且第二批每盆的价格比第一批的少10元.则第二批绿植每盆的价格
15. 在“校园文化”建设中,某校用8 000元购进一批绿色植物,种植在礼堂前的空地处.根据建设方案的要求,该校又用7500元购进第二批绿植植物.若两次所买植物的盆数相同,且第二批每盆的价格比第一批的少10元.则第二批绿植每盆的价格为元.
16. 如图,在菱形ABCD中,AB=4,取CD中点O , 以O为圆心OD为半径作圆交AD于E , 交BC的延长线交于点F ,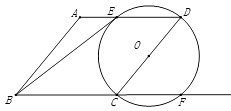 (1)、若 ,则菱形ABCD的面积为;(2)、当BE与圆相切时,AE= .
(1)、若 ,则菱形ABCD的面积为;(2)、当BE与圆相切时,AE= .三、解答题
-
17. 计算题(1)、计算: .(2)、化简: .18.
△ABC在平面直角坐标系中的位置如图所示.
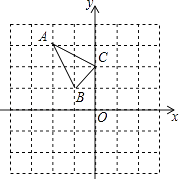 (1)、作△ABC关于原点O成中心对称的△A1B1C1 .(2)、请写出点B关于y轴对称的点B2的坐标 . 若将点B2向下平移h单位,使其落在△A1B1C1内部(不包括边界),直接写出h的值(写出满足的一个即可).19. 如图,△ABC为等边三角形,过点B作BD⊥AC于点D , 过D作DE∥BC , 且DE=CD , 连接CE ,
(1)、作△ABC关于原点O成中心对称的△A1B1C1 .(2)、请写出点B关于y轴对称的点B2的坐标 . 若将点B2向下平移h单位,使其落在△A1B1C1内部(不包括边界),直接写出h的值(写出满足的一个即可).19. 如图,△ABC为等边三角形,过点B作BD⊥AC于点D , 过D作DE∥BC , 且DE=CD , 连接CE ,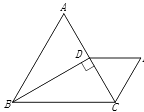 (1)、求证:△CDE为等边三角形;(2)、请连接BE , 若AB=4,求BE的长.20. 某调查机构将今年温州市民最关注的热点话题分为消费、教育、环保、反腐及其它共五类.根据最近一次随机调查的相关数据,绘制的统计图表如下:
(1)、求证:△CDE为等边三角形;(2)、请连接BE , 若AB=4,求BE的长.20. 某调查机构将今年温州市民最关注的热点话题分为消费、教育、环保、反腐及其它共五类.根据最近一次随机调查的相关数据,绘制的统计图表如下:
根据以上信息解答下列问题:
(1)、本次共调查人 ,请在补全条形统计图并标出相应数据 ;(2)、若温州市约有900万人口,请你估计最关注教育问题的人数约为多少万人?(3)、在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,求抽取的两人恰好是甲和乙的概率(列树状图或列表说明).21. 如图,点C在以AB为直径的⊙O上,过C作⊙O的切线交AB的延长线于E , AD⊥CE于D , 连结AC.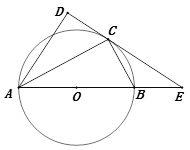 (1)、求证:AC平分∠BAD.(2)、若tan∠CAD= ,AD=8,求⊙O直径AB的长.22. 某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部分无条件舍去) .(1)、下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
(1)、求证:AC平分∠BAD.(2)、若tan∠CAD= ,AD=8,求⊙O直径AB的长.22. 某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部分无条件舍去) .(1)、下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,电量(度)
电费(元)
A
240
B
合计
90
(2)、若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?23. 如图,抛物线 交x轴的正半轴于点A , 点B( ,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC , 以AB、BC为邻边作▱ABCD,记点C纵坐标为n ,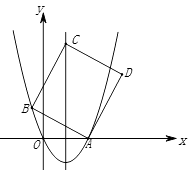 (1)、求a的值及点A的坐标;(2)、当点D恰好落在抛物线上时,求n的值;(3)、 记CD与抛物线的交点为E,连接AE,BE,当三角形AEB的面积为7时,n=
(1)、求a的值及点A的坐标;(2)、当点D恰好落在抛物线上时,求n的值;(3)、 记CD与抛物线的交点为E,连接AE,BE,当三角形AEB的面积为7时,n=
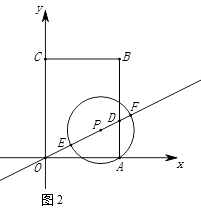
24. 如图1,直角坐标系中有一矩形OABC , 其中 O是坐标原点,点A , C分别在x轴和y轴上,点B的坐标为(3,4),直线 交AB于点D , 点P是直线 位于第一象限上的一点,连接PA , 以PA为半径作⊙P ,
 (1)、连接AC , 当点P落在AC上时, 求PA的长;(2)、当⊙P经过点O时,求证:△PAD是等腰三角形;(3)、设点P的横坐标为m ,
(1)、连接AC , 当点P落在AC上时, 求PA的长;(2)、当⊙P经过点O时,求证:△PAD是等腰三角形;(3)、设点P的横坐标为m ,在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;