2017年辽宁省大连市高考数学一模试卷（理科）

试卷更新日期：2017-04-27 类型：高考模拟

进入出卷网下载

一、选择题：

1. 已知复数z=1+2i，则 $z \cdot \bar{z}$ =（）

A、5 B、5+4i C、﹣3 D、3﹣4i

查看试题解析
2. 已知集合A={x|x²﹣2x﹣3＜0}， $B = {x | \frac{1 - x}{x} < 0}$ ，则A∩B=（）

A、{x|1＜x＜3} B、{x|﹣1＜x＜3} C、{x|﹣1＜x＜0或0＜x＜3} D、{x|﹣1＜x＜0或1＜x＜3}

查看试题解析
3. 设a，b均为实数，则“a＞|b|”是“a³＞b³”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 若点P为抛物线 $C ： x^{2} = \frac{1}{2} y$ 上的动点，F为抛物线C的焦点，则|PF|的最小值为（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、 $\frac{1}{8}$

查看试题解析
5. 已知数列{a_n}满足a_n₊₁﹣a_n=2，a₁=﹣5，则|a₁|+|a₂|+…+|a₆|=（）

A、9 B、15 C、18 D、30

查看试题解析
6. 在平面内的动点（x，y）满足不等式 ${\begin{matrix} x + y - 3 \leq 0 \\ x - y + 1 \geq 0 \\ y \geq 0 \end{matrix}$ ，则z=2x+y的最大值是（）

A、6 B、4 C、2 D、0

查看试题解析
7. 某几何体的三视图如图所示，则其体积为（）

A、4 B、 $\frac{7}{3}$ C、 $\frac{4}{3}$ D、 $\frac{8}{3}$

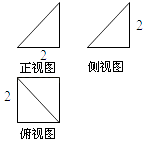查看试题解析
8. 将一枚硬币连续抛掷n次，若使得至少有一次正面向上的概率不小于 $\frac{15}{16}$ ，则n的最小值为（）

A、4 B、5 C、6 D、7

查看试题解析
9. 运行如图所示的程序框图，则输出结果为（）

A、 $\frac{11}{8}$ B、 $\frac{5}{4}$ C、 $\frac{3}{2}$ D、 $\frac{23}{16}$

查看试题解析
10. 若方程 $2 \sin (2 x + \frac{π}{6}) = m$ 在 $x \in [0 ， \frac{π}{2}]$ 上有两个不相等的实数解x₁ ， x₂ ，则x₁+x₂=（）

A、 $\frac{π}{2}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
11. 已知向量 $\vec{O A} = (3 ， 1)$ ， $\vec{O B} = (- 1 ， 3)$ ， $\vec{O C} = m \vec{O A} - N \vec{O B}$ （m＞0，n＞0），若m+n∈[1，2]，则 $| \vec{O C} |$ 的取值范围是（）

A、 $[\sqrt{5} ， 2 \sqrt{5}]$ B、 $[\sqrt{5} ， 2 \sqrt{10})$ C、 $(\sqrt{5} ， \sqrt{10})$ D、 $[\sqrt{5} ， 2 \sqrt{10}]$

查看试题解析
12. 已知定义在R上的函数f（x）=e^x+mx²﹣m（m＞0），当x₁+x₂=1时，不等式f（x₁）+f（0）＞f（x₂）+f（1）恒成立，则实数x₁的取值范围是（）

A、（﹣∞，0） B、 $(0 ， \frac{1}{2})$ C、 $(\frac{1}{2} ， 1)$ D、（1，+∞）

查看试题解析

二、填空题

13. 现将5张连号的电影票分给甲乙等5个人，每人一张，且甲乙分得的电影票连号，则共有种不同的分法（用数字作答）．

查看试题解析
14. 函数f（x）=e^x•sinx在点（0，f（0））处的切线方程是．

查看试题解析
15. 我国古代数学专著《孙子算法》中有“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”如果此物数量在100至200之间，那么这个数．

查看试题解析
16. 过双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的焦点F且与一条渐近线垂直的直线与两条渐近线相交于A，B两点，若 $\vec{B F} = 2 \vec{F A}$ ，则双曲线的离心率为．

查看试题解析

三、解答题

17. 已知点 $P (\sqrt{3} ， 1)$ ，Q（cosx，sinx），O为坐标原点，函数 $f (x) = \vec{O P} \cdot \vec{Q P}$ ．

(1)、求函数f（x）的最小值及此时x的值；

(2)、若A为△ABC的内角，f（A）=4，BC=3，求△ABC的周长的最大值．

查看试题解析
18. 某手机厂商推出一次智能手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如下：
女性用户
分值区间
[50，60）
[60，70）
[70，80）
[80，90）
[90，100）
频数
20
40
80
50
10
男性用户
分值区间
[50，60）
[60，70）
[70，80）
[80，90）
[90，100）
频数
45
75
90
60
30

(1)、完成下列频率分布直方图，并比较女性用户和男性用户评分的方差大小（不计算具体值，给出结论即可）；

(2)、根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意取3名用户，求3名用户评分小于90分的人数的分布列和期望．

查看试题解析
19. 如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，PA⊥底面ABCD，AD=AP，E为棱PD中点．

(1)、求证：PD⊥平面ABE；

(2)、若F为AB中点， $\vec{P M} = λ \vec{P C} (0 < λ < 1)$ ，试确定λ的值，使二面角P﹣FM﹣B的余弦值为- $\frac{\sqrt{3}}{3}$ ．

查看试题解析
20. 已知点P是长轴长为 $2 \sqrt{2}$ 的椭圆Q： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上异于顶点的一个动点，O为坐标原点，A为椭圆的右顶点，点M为线段PA的中点，且直线PA与OM的斜率之积恒为 $- \frac{1}{2}$ ．

(1)、求椭圆Q的方程；

(2)、设过左焦点F₁且不与坐标轴垂直的直线l交椭圆于C，D两点，线段CD的垂直平分线与x轴交于点G，点G横坐标的取值范围是 $[- \frac{1}{4} ， 0)$ ，求|CD|的最小值．

查看试题解析
21. 已知函数f（x）=（x﹣2）e^x+a（x+2）²（x＞0）．

(1)、若f（x）是（0，+∞）的单调递增函数，求实数a的取值范围；

(2)、当 $a \in (0 ， \frac{1}{4})$ 时，求证：函数f（x）有最小值，并求函数f（x）最小值的取值范围．

查看试题解析
22. 已知在平面直角坐标系xOy中，以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C₁的极坐标方程为ρ=4cosθ，直线l的参数方程为 ${\begin{matrix} x = 1 - \frac{2 \sqrt{5}}{5} t \\ y = 1 + \frac{\sqrt{5}}{5} t \end{matrix}$ （t为参数）．

(1)、求曲线C₁的直角坐标方程及直线l的普通方程；

(2)、若曲线C₂的参数方程为 ${\begin{matrix} x = 2 \cos α \\ y = \sin α \end{matrix}$ （α为参数），曲线C₁上点P的极角为 $\frac{π}{4}$ ，Q为曲线C₂上的动点，求PQ的中点M到直线l距离的最大值．

查看试题解析
23. 已知a＞0，b＞0，函数f（x）=|x+a|+|2x﹣b|的最小值为1．

(1)、求证：2a+b=2；

(2)、若a+2b≥tab恒成立，求实数t的最大值．

查看试题解析

女性用户	分值区间	[50，60）	[60，70）	[70，80）	[80，90）	[90，100）
女性用户	频数	20	40	80	50	10
男性用户	分值区间	[50，60）	[60，70）	[70，80）	[80，90）	[90，100）
男性用户	频数	45	75	90	60	30