2017届浙江省湖州市七校联考中考数学模拟试题
试卷更新日期:2017-04-27 类型:中考模拟
一、选择题
-
1. |-2|=( )A、2 B、-2 C、2 D、2. 下列计算正确的是()A、 B、 C、 D、3. 支付宝与“滴滴打车”联合推出优惠,“滴滴打车”一夜之间红遍大江南北.据统计,2016年“滴滴打车”账户流水总金额达到4730000000元,用科学记数法表示数为( )A、 B、 C、 D、4. 如图,△ABC,∠B=90°,AB=3,BC=4,则cosA等于( )
 A、 B、 C、 D、5. 不等式组 的最小整数解是( )
A、 B、 C、 D、5. 不等式组 的最小整数解是( )
A、1 B、2 C、3 D、46. 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=60°,则∠2等于( )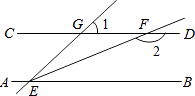 A、130° B、140° C、150° D、160°7. 如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )
A、130° B、140° C、150° D、160°7. 如图所示的支架是由两个长方体构成的组合体,则它的主视图是( ) A、
A、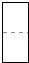 B、
B、 C、
C、 D、
D、 8. 在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
8. 在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:成 绩
45
46
47
48
49
50
人 数
1
2
4
2
5
1
这此测试成绩的中位数和众数分别为( )
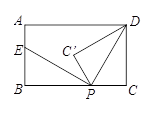
A、47, 49 B、48, 49 C、47.5, 49 D、48, 509.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C’处;作∠BPC’的角平分线交AB于点E . 设BP=x , BE=y , 则下列图象中,能表示y与x的函数关系的图象大致是( )
 A、
A、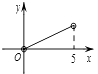 B、
B、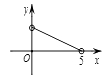 C、
C、 D、
D、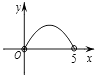 10.
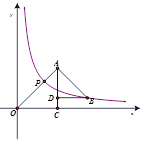
10.如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数 在第一象限的图像经过点B,与OA交于点P,若OA2-AB2=18,则点P的横坐标为( )
 A、9 B、6 C、3 D、3
A、9 B、6 C、3 D、3二、填空题
-
11. 分解因式: =.12. 二次根式 中,x的取值范围是 .13. 已知实数x,y满足|x-4|+=0,则以x,y的值为两边长的等腰三角形的周长是.
14.如图,在⊙O中,CD是直径,弦AB⊥CD , 垂足为E , 若∠C=22.5°,AB=6 cm,则阴影部分面积为cm2。
 15.
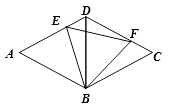
15.如图,在边长为2的菱形ABCD中, ∠ABC=120°, E , F分别为AD , CD上的动点,且AE+CF=2,则线段EF长的最小值是 .
 16.
16.如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,
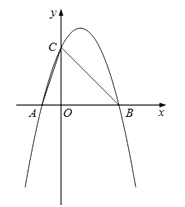 (1)、将抛物线沿y轴向下平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,则t的取值范围是.(2)、抛物线上存在点P,使∠BCP=∠BAC﹣∠ACO,则点P的坐标为 .
(1)、将抛物线沿y轴向下平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,则t的取值范围是.(2)、抛物线上存在点P,使∠BCP=∠BAC﹣∠ACO,则点P的坐标为 .
三、解答题
-
17. 计算: -18.
如图,▱ABCD中,E是AD的中点,连接CE并延长,与BA的延长线交于点F. 请你找出图中与AF相等的一条线段,并加以证明.(不再添加其它线段,不再标注或使用其它字母)
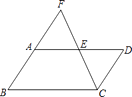 (1)、结论:AF= .(2)、证明你的结论。
(1)、结论:AF= .(2)、证明你的结论。
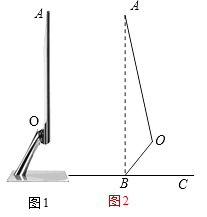
19.如图,图①是某电脑液晶显示器的侧面图,显示屏AO可以绕点O旋转一定的角度.研究表明:显示屏顶端A与底座B的连线AB与水平线BC垂直时(如图②),人观看屏幕最舒适.此时测得∠BAO=15°,AO=30cm,∠OBC=45°,求AB的长度.(结果精确到1 cm)(参考数据:sin15°≈0.26,cos15°≈0.97, tan15°≈0.27, ≈1.414)
 20.
20.李老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
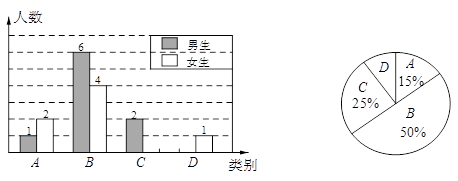 (1)、李老师一共调查了多少名同学?(2)、C类女生有名,D类男生有名,将下面条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行
(1)、李老师一共调查了多少名同学?(2)、C类女生有名,D类男生有名,将下面条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
21.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
 (1)、求证:∠BDC=∠A;(2)、若CE=2 ,DE=2,求AD的长,
(1)、求证:∠BDC=∠A;(2)、若CE=2 ,DE=2,求AD的长,
(3)、在(2)的条件下,求弧BD的长。22. 某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:销售量n(件)
n=50﹣x
销售单价m(元/件)
当1≤x≤20时,
当21≤x≤30时,
(1)、请计算第15天该商品单价为多少元/件?(2)、求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)、这30天中第几天获得的利润最大?最大利润是多少?23.如图1,在Rt△ABC中,∠ACB=90°,AC=BC,在斜边AB上取一点D,过点D作DE//BC,交AC于点E.现将△ADE绕点A旋转一定角度到如图2所示的位置(点D在△ABC的内部),使得∠ABD+∠ACD=90°.
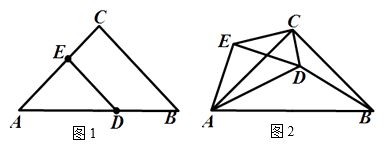 (1)、①求证:△ABD∽△ACE;
(1)、①求证:△ABD∽△ACE;②若CD=1,BD= ,求AD的长;
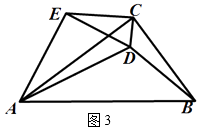
(2)、如图3,将原题中的条件“AC=BC”去掉,其它条件
不变,设 ,若CD=1,BD=2,AD=3,求k的值;
 (3)、
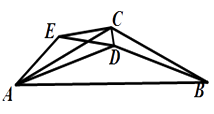
(3)、如图4,将原题中的条件“∠ACB=90°”去掉,其它条件不变,若 ,设CD=m , BD=n , AD=p , 试探究m , n , p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)
 24.
24.如图,在平面直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC.点E是y轴上任意一点记点E为(0,n).
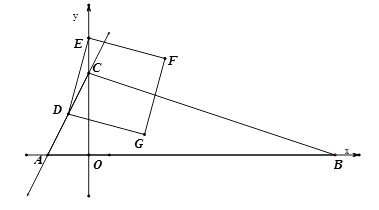 (1)、求点D的坐标及直线BC的解析式;(2)、连结DE,将线段DE绕点D按顺时针旋转90°得线段DG,作正方形DEFG,是否存在n的值,使正方形的顶点F落在△ABC的边上?若存在,求出所有满足条件的n的值;若不存在,说明理由.
(1)、求点D的坐标及直线BC的解析式;(2)、连结DE,将线段DE绕点D按顺时针旋转90°得线段DG,作正方形DEFG,是否存在n的值,使正方形的顶点F落在△ABC的边上?若存在,求出所有满足条件的n的值;若不存在,说明理由.
(3)、作点E关于AC的对称点E’,当n为何值时,A E’分别于AC,BC,AB垂直?