数学(苏科版)七年级下册第11章 11.6一元一次不等式组 同步练习
试卷更新日期:2017-04-27 类型:同步测试
一、单选题
-
1. 不等式组 的整数解是( )A、15 B、16 C、17 D、15,162. 不等式组 的解集在数轴上表示正确的是( )A、
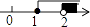 B、
B、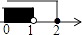 C、
C、 D、
D、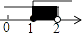 3. 若方程组 的解x,y满足0<x+y<1,则k的取值范围是( )A、﹣1<k<0 B、﹣4<k<﹣1 C、0<k<1 D、k>﹣44. 若关于x的不等式组 的整数解共有4个,则a的取值范围是 ( )
3. 若方程组 的解x,y满足0<x+y<1,则k的取值范围是( )A、﹣1<k<0 B、﹣4<k<﹣1 C、0<k<1 D、k>﹣44. 若关于x的不等式组 的整数解共有4个,则a的取值范围是 ( )
A、6<a<7 B、6≤a<7 C、6≤a≤7 D、6<a≤75. 关于x的不等式组 的解集为x<3,那么m的取值范围为( )A、m=3 B、m>3 C、m<3 D、m≥36. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 若点P(a,a﹣2)在第四象限,则a的取值范围是( )A、0<a<2 B、﹣2<a<0 C、a>2 D、a<08. 若关于x的一元一次不等式组 无解,则a的取值范围是( )A、a≥1 B、a>1 C、a≤﹣1 D、a<﹣19. 把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本,在共有学生人数为( )A、6人 B、5人 C、6人或5人 D、4人
7. 若点P(a,a﹣2)在第四象限,则a的取值范围是( )A、0<a<2 B、﹣2<a<0 C、a>2 D、a<08. 若关于x的一元一次不等式组 无解,则a的取值范围是( )A、a≥1 B、a>1 C、a≤﹣1 D、a<﹣19. 把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本,在共有学生人数为( )A、6人 B、5人 C、6人或5人 D、4人二、填空题
-
10. 不等式组 的解集是 .11. 定义新运算:对于任意实数a,b都有a△b=ab﹣a﹣b+1,等式右边是通常的加法、减法及乘法运算,例如:2△4=2×4﹣2﹣4+1=8﹣6+1=3,请根据上述知识解决问题:若3△x的值大于5而小于9,则x的取值范围为12. 已知关于x的不等式组 的整数解共有5个,则a的取值范围是 .13. 有学生若干人,住若干间宿舍,若每间住4人,则有20人无法安排住宿,若每间住8人,则最后有一间宿舍不满也不空,则学生人数为人.
三、计算题
-
14. 解不等式组 ,并写出该不等式组的整数解.
四、解答题
-
15. 解不等式组 ,并写出整数解.16. 解不等式组 ,并把解集在数轴上表示出来.17. 已知关于x、y的方程组 的解是一对正数,求a的取值范围.18. 若不等式组 ,的整数解是关于x的方程2x-4=ax的根,求a的值.
19. 解不等式组: ,并在数轴上表示出不等式组的解集.20. 已知关于x、y的二元一次方程组 的解满足不等式组 ,则m的取值范围是什么?五、综合题
-