数学（苏科版）七年级下册第7章 7.5多边形的内角和与外角和 同步练习
试卷更新日期：2017-04-27 类型：同步测试
一、单选题
-
1. 如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变．请试着找一找这个规律，你发现的规律是（ ）
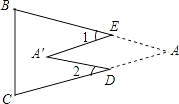A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2（∠1+∠2）2. 如图，在△ABC中，∠C=50°，按图中虚线将∠C剪去后，∠1+∠2等于（ ）
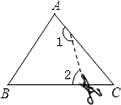A、230° B、210° C、130° D、310°3. 已知一个多边形的内角和等于它的外角和的两倍，则这个多边形的边数为（ ）
A、6 B、7 C、8 D、94.如图，△ABC， ∠ABC、∠ACB的三等分线交于点E、D，若∠BFC=132°，∠BGC=118°，则∠A的度数为（ ）
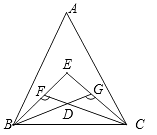A、65° B、66° C、70° D、78°5. 如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，这个规律是（ ）
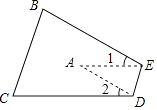A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2（∠1+∠2）6. 在△ABC中，∠A，∠B都是锐角，则∠C是（ ）A、锐角 B、直角 C、钝角 D、以上都有可能7. 从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是（ ）A、6 B、7 C、8 D、9二、填空题
-
8. 七边形的内角和是度．9.
在△ABC中，∠C=50°，按图中虚线将∠C剪去后，∠1+∠2等于度.
10. 一个多边形的内角和是1800°，这个多边形是边形．11.如图，把一副常用的三角板如图所示拼在一起，那么图中∠ABF= ．
12.如图，小明在操场上从A点出发，沿直线前进10米后向左转40°，再沿直线前进10米后，又向左转40°，照这样走下去，他第一次回到出发地A点时，一共走了米．
13. 一个十边形所有内角都相等，它的每一个外角等于度．14. 如图所示，求∠A+∠B+∠C+∠D+∠E+∠F= ．
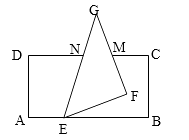
15. 如果等腰三角形一腰上的高与另一腰的夹角为45°，那么这个等腰三角形的底角度数为 ．16.如图，将一张长方形纸片与一张直角三角形纸片(∠EFG＝90°)按如图所示的位置摆放，
使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上，已知∠BEF＝21°，则
∠CMF＝ ．
三、计算题
-
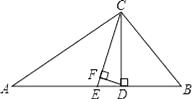
17.
如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，求∠CDF的度数．
四、解答题
-
18. 一个多边形，它的内角和比外角和的4倍多180°，求这个多边形的边数及内角和度数．19. 一个多边形，除一个内角外，其余各内角之和等于2012°，求这个内角的度数及多边形的边数．20.
如图①，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．
(1)、探究猜想：①若∠A=20°，∠D=40°，则∠AED=
②猜想图①中∠AED，∠EAB，∠EDC的关系，并用两种不同的方法证明你的结论．
(2)、拓展应用：如图②，射线FE与l1 ， l2交于分别交于点E、F，AB∥CD，a，b，c，d分别是被射线FE隔开的4个区域（不含边界，其中区域a，b位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（任写出两种，可直接写答案）．
五、综合题
-
21. 如图，六边形ABCDEF的内角都相等，CF∥AB．
(1)、求∠FCD的度数；(2)、求证：AF∥CD．22. 实验探究：(1)、动手操作：
①如图1，将一块直角三角板DEF放置在直角三角板ABC上，使三角板DEF的两条直角边DE、DF分别经过点B、C，且BC∥EF，已知∠A=30°，则∠ABD+∠ACD=；
②如图2，若直角三角板ABC不动，改变等腰直角三角板DEF的位置，使三角板DEF的两条直角边DE、DF仍然分别经过点B、C，那么∠ABD+∠ACD=
(2)、猜想证明：如图3，∠BDC与∠A、∠B、∠C之间存在着什么关系，并说明理由；
(3)、灵活应用：请你直接利用以上结论，解决以下列问题：
①如图4，BE平分∠ABD，CE平分∠ACB，若∠BAC=40°，∠BDC=120°，求∠BEC的度数；
(4)、②如图5，∠ABD，∠ACD的10等分线相交于点F1、F2、…、F9 ，若∠BDC=120°，∠BF3C=64°，则∠A的度数为 ．
-