湖南省永州市2018-2019高三上学期文数第二次模拟考试试卷

试卷更新日期：2019-03-18 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = R$ ，集合 $A = {x | 0 \leq x < 2}$ ，则 $C_{U} A =$ （）

A、 B、 C、 D、

查看试题解析
2. 为了得到函数 $y = sin (x - \frac{π}{3})$ 的图像，只需将函数 $y = sin x$ 的图像（）

A、向右平移 $\frac{π}{6}$ 个单位 B、向右平移 $\frac{π}{3}$ 个单位 C、向左平移 $\frac{π}{6}$ 个单位 D、向左平移 $\frac{π}{3}$ 个单位

查看试题解析
3. 若复数 $z = \frac{2}{1 + i}$ （ $i$ 为虚数单位），则复数 $z$ 在坐标平面内对应点的坐标为（）

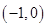A、 B、 C、 D、

查看试题解析
4. 若直线 $y = k (x - 2)$ 与圆 $x^{2} + y^{2} = 1$ 相切，则 $k =$ （）

A、1 B、 C、 D、

查看试题解析
5. 已知抛物线 $y^{2} = 4 x$ 上的点 $M$ 到焦点的距离为5，则点 $M$ 的横坐标为（）

A、1 B、4 C、6 D、10

查看试题解析
6. 在 $R t Δ A B C$ 中， $∠ C = 90^{0}$ ， $A C = 2$ ， $B C = 1$ ，则 $\overset{⇀}{A B} \cdot \overset{⇀}{C B} =$ （）

A、-2 B、0 C、1 D、2

查看试题解析
7. “不等式 $x^{2} - x + m > 0$ 在 $R$ 上恒成立”的充要条件是（）

A、 B、 C、 D、

查看试题解析
8. 已知函数 $f (x) = a {(sin ω x + cos ω x)}^{2} (a > 0)$ 的最小正周期为 $π$ ，最大值为2，则（）

A、 B、 C、 D、

查看试题解析
9. 若函数 $f (x) = 2^{| x |} - k$ 存在零点，则 $k$ 的取值范围是（）

A、 B、 C、 $k < 1$ D、

查看试题解析
10. 某几何体的三视图如图所示，图中三角形均是边长为2的正三角形，几何体表面上的点 $M$ 对应正视图中的点 $A$ ，几何体表面上的点 $N$ 对应侧视图中的点 $B$ ，则几何体中线段 $M N$ 的长度为（）

A、1 B、2 C、 D、 $2 \sqrt{2}$

查看试题解析
11. 若 $\exists a > 0$ ，使得函数 $f (x) = 3 a^{2} ln x$ 与 $g (x) = \frac{1}{2} x^{2} - 2 a x - b$ 的图像有公共点，且它们在公共点处的切线相同，则实数 $b$ 的最大值为（）

A、 B、 C、 D、

查看试题解析

二、填空题

12. 若 ${log}_{2} a > 1$ ，则 $a$ 的取值范围是．

查看试题解析
13. 若实数 $x ， y$ 满足 ${\begin{matrix} x \leq 1 \\ y \leq 1 \\ x + y \geq 1 \end{matrix}$ ，则点 $(x ， y)$ 到原点的最大距离为．

查看试题解析
14. 已知一平面截球 $O$ 所得截面圆的半径为1，且球心到截面圆所在平面的距离为2，则球 $O$ 的表面积为．

查看试题解析
15. 在三角形 $A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ， $A = 30^{0}$ ， $C = 45^{0}$ ， $c = 3$ ，点 $P$ 是平面 $A B C$ 内的一个动点，若 $∠ B P C = 60^{0}$ ，则 $Δ P B C$ 面积的最大值是．

查看试题解析

三、解答题

16. 已知公差不为0的等差数列 ${a_{n}}$ 满足 $a_{3} = 9$ ， $a_{2}$ 是 $a_{1}$ ， $a_{7}$ 的等比中项.

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设数列 ${b_{n}}$ 满足 $b_{n} = \frac{1}{n (a_{n} + 7)}$ ，求 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
17. 如图，在三棱锥 $P - A B C$ 中， $P A ⊥$ 平面 $A B C$ ， $A B = B C = 2$ ，点 $M$ 为线段 $A C$ 的中点.

(1)、证明：平面 $P A C ⊥$ 平面 $P M B$ ；

(2)、若 $∠ A B C = 60^{0}$ ，直线 $P C$ 与平面 $A B C$ 所成角为 $60^{0}$ ，求三棱锥 $P - A B M$ 的体积.

查看试题解析
18. 为了落实习总书记在改革开放40周年庆祝大会上的讲话精神，实现“更高质量、更有效率”的可持续发展，继续深化改革，某工业基地对在生产同一产品的甲、乙两个厂区，选择了乙厂区进行改革试点，一段时间后，工业基地为了检查甲、乙两个厂区的生产情况，随机地从这两厂区生产的大量产品中各抽取100件作为样本，得到关于产品质量指标值的频数分布表（已知合格产品的质量指标值应在区间 $（ 2.55 ， 2.70]$ 内，否则为不合格产品）：

(1)、将频率视为概率，由表中的数据分析，若在某个时间段内甲、乙两个厂区均生产了2000件产品，则在此时间段内甲、乙两个厂区生产出的不合格产品分别为多少件？

(2)、根据样本数据写出下面 $2 \times 2$ 列联表中 $a ， b ， c ， d$ 的值，判断是否有 $85 %$ 的把握认为“该工业基地的产品质量与改革有关”，并说明理由.

查看试题解析
19. 已知动点 $M$ 到两定点 $F_{1} (- m, 0)$ ， $F_{2} (m, 0)$ 距离之和为4（ $0 < m < 2$ ），且动点 $M$ 的轨迹曲线 $C$ 过点 $N (\sqrt{3}, \frac{1}{2})$ .

(1)、求 $m$ 的值；

(2)、若直线 $l : y = k x + \sqrt{2}$ 与曲线 $C$ 有不同的两个交点 $A, B$ ，且 $\overset{⇀}{O A} \cdot \overset{⇀}{O B} = 2$ （ $O$ 为坐标原点），求 $k$ 的值.

查看试题解析
20. 已知函数 $f (x) = x - a ln x (a > 0)$ ， $g (x) = x^{3} - 16 x + 20$ .

(1)、讨论函数 $f (x)$ 在 $(\frac{1}{a} ， + \infty)$ 上的单调性；

(2)、设 $h (x) = x^{2} f (x) + g (x)$ ，当 $a = 1$ 时，证明： $h (x) > 0$ .

查看试题解析
21. 在直角坐标系 $x O y$ 中，过点 $M (x_{0}, y_{0})$ 的直线 $l$ 的参数方程为 ${\begin{matrix} x = x_{0} + \frac{\sqrt{2}}{2} t \\ y = y_{0} + \frac{\sqrt{2}}{2} t \end{matrix}$ （ $t$ 为参数），以坐标原点 $O$ 为极点，以 $x$ 轴正半轴为极轴建立极坐标系，曲线 $C$ 的极坐标方程为 $ρ = 1$ .

(1)、若点 $M$ 的直角坐标为 $(1, \sqrt{3})$ ，求直线 $l$ 及曲线 $C$ 的直角坐标方程；

(2)、若点 $M$ 在圆 $x^{2} + y^{2} = 4$ 上，直线 $l$ 与 $C$ 交于 $A, B$ 两点，求 $| M A | \cdot | M B |$ 的值.

查看试题解析
22. 已知函数 $f (x) = | 2 x - 1 | + | 2 x - a |$ .

(1)、当 $a = 1$ 时，求不等式 $f (x) \geq 2 x$ 的解集；

(2)、若 $y = f (x)$ 的最小值为1，求实数 $a$ 的值.

查看试题解析