湖北省黄冈市2018-2019学年高三上学期文数元月调研试卷
试卷更新日期:2019-03-18 类型:高考模拟
一、单选题
-
1. 复数z满足 ,则z的其轭复数 对应的点是第 象限的点A、一 B、二 C、三 D、四2. 已知函数 的定义域为 ,则 的定义域为A、
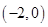 B、
B、 C、
C、 D、
D、 3. 关于x的不等式 的解集是 ,则关于x的不等式 的解集是A、
3. 关于x的不等式 的解集是 ,则关于x的不等式 的解集是A、 B、
B、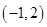 C、
C、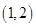 D、
D、 4. 过点 的直线在两坐标轴上的截距相等,则该直线方程为A、
4. 过点 的直线在两坐标轴上的截距相等,则该直线方程为A、 B、
B、 C、 或
C、 或  D、 或
D、 或  5. 下列有关命题的叙述错误的是A、若“
5. 下列有关命题的叙述错误的是A、若“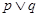 ”为假命题,则p与q均为假命题
B、已知向量
”为假命题,则p与q均为假命题
B、已知向量  ,
,  ,则“
,则“  ”是“
”是“  ”的充分不必要条件
C、命题“若
”的充分不必要条件
C、命题“若  ,则 的逆否命题为“若
,则 的逆否命题为“若 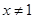 ,则
,则  ”
D、命题“
”
D、命题“  ,
,  ”的否定是“
”的否定是“  ,
,  ”
6. 已知角 的顶点与原点重合,始边与 轴的正半轴重合,终边在直线 上,则A、
”
6. 已知角 的顶点与原点重合,始边与 轴的正半轴重合,终边在直线 上,则A、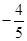 B、
C、
D、
7. 已知P为 所在平面内一点,且满足 , ,则A、 B、 C、 D、
B、
C、
D、
7. 已知P为 所在平面内一点,且满足 , ,则A、 B、 C、 D、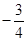 8. 已知圆 关于 对称,则 的值为A、 B、1 C、 D、09. 已知a,b,c分别为 的三个内角A,B,C的对边,已知 , , ,若满足条件的三角形有两个,则x的取值范围是
8. 已知圆 关于 对称,则 的值为A、 B、1 C、 D、09. 已知a,b,c分别为 的三个内角A,B,C的对边,已知 , , ,若满足条件的三角形有两个,则x的取值范围是
A、 B、
B、 C、
D、
C、
D、 10. 黄冈市的天气预报显示,大别山区在今后的三天中,每一天有强浓雾的概率为 ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率:先利用计算器产生 之间整数值的随机数,并用0,1,2,3,4,5表示没有强浓雾,用6,7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
10. 黄冈市的天气预报显示,大别山区在今后的三天中,每一天有强浓雾的概率为 ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率:先利用计算器产生 之间整数值的随机数,并用0,1,2,3,4,5表示没有强浓雾,用6,7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:779 537 113 730 588 506 027 394 357 231
683 569 479 812 842 273 925 191 978 520
则这三天中至少有两天有强浓雾的概率近似为
A、 B、 C、 D、11. 已知圆 与函数 的图象有唯一交点,且交点的横坐标为 ,则 ( )A、 B、2 C、 D、3二、填空题
-
12. 如图是为了求出满足 的最小整数n,
 和
和  两个空白框中,可以分别填入
两个空白框中,可以分别填入  A、
A、 ?,输出
?,输出  B、
B、 ?,输出n
C、
?,输出n
C、 ?,输出
?,输出  D、
D、 ?,输出n
13. 自2015年来黄冈市各重点高中开展了形式多样的各种选课走班活动,记者调查了黄梅一中甲、乙、丙三位同学,在被问到是否参加过黄梅戏、黄梅挑花、岳家拳这三个特长班时,甲说:我参加过的特长班比乙多,但没有参加过岳家拳;乙说:我没有参加过黄梅挑花;丙说:我们三个人都参加过同一个特长班,由此判断乙参加过的特长班为 .14. 在等边三角形ABC中, 在 方向上投影为 ,且 ,则 的面积为 .15. 若关于x的不等式 在 上恒成立,则实数a的最小值为 .16. 意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:1,1,2,3,5,8,该数列的特点是:前两个数均为1,从第三个数起,每一个数都等于它前面两个数的和,人们把这样的一列数所组成的数列 称为“斐波那契数列”,则 .
?,输出n
13. 自2015年来黄冈市各重点高中开展了形式多样的各种选课走班活动,记者调查了黄梅一中甲、乙、丙三位同学,在被问到是否参加过黄梅戏、黄梅挑花、岳家拳这三个特长班时,甲说:我参加过的特长班比乙多,但没有参加过岳家拳;乙说:我没有参加过黄梅挑花;丙说:我们三个人都参加过同一个特长班,由此判断乙参加过的特长班为 .14. 在等边三角形ABC中, 在 方向上投影为 ,且 ,则 的面积为 .15. 若关于x的不等式 在 上恒成立,则实数a的最小值为 .16. 意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:1,1,2,3,5,8,该数列的特点是:前两个数均为1,从第三个数起,每一个数都等于它前面两个数的和,人们把这样的一列数所组成的数列 称为“斐波那契数列”,则 .三、解答题
-
17. 已知函数
 (1)、用“五点作图法”在给定的坐标系中,画出函数 在 上的图象.(2)、先将函数 的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数 的图象,求 的对称中心.18. 设 , 或 , ; 函数 在 上为增函数,若 ”为假,且“ ”为真,求实数 的取值范围.19. 中国人旅游有个特点:喜欢在旅游区购买当地的名优土特产,黄冈市有很多名优土特产,黄冈市的蕲春县就有闻名于世的“蕲春四宝” 蕲竹、蕲艾、蕲蛇、蕲龟 ,由于医圣李时珍出生在蕲春县,很多人慕名而来,回家时顺带买点“蕲春四宝”,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:
(1)、用“五点作图法”在给定的坐标系中,画出函数 在 上的图象.(2)、先将函数 的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数 的图象,求 的对称中心.18. 设 , 或 , ; 函数 在 上为增函数,若 ”为假,且“ ”为真,求实数 的取值范围.19. 中国人旅游有个特点:喜欢在旅游区购买当地的名优土特产,黄冈市有很多名优土特产,黄冈市的蕲春县就有闻名于世的“蕲春四宝” 蕲竹、蕲艾、蕲蛇、蕲龟 ,由于医圣李时珍出生在蕲春县,很多人慕名而来,回家时顺带买点“蕲春四宝”,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:男
女
总计
事先知道“蕲春四宝”
8
n
q
事先不知道“蕲春四宝”
m
4
36
总计
40
p
t
附:
(1)、写出列联表中各字母代表的数字;(2)、由以上列联表判断,能否在犯错误的概率不超过 的前提下认为购买“蕲春四宝”和是否“事先知道 蕲春四宝 有关系”?(3)、现从这60名游客中用分层抽样的方法抽取15名游客进行问卷调查,再从抽取的女游客中,随机选出2人给予小礼品,求有2名女游客是事先知道“蕲春四宝”的概率?20. 设正项数列 的前 项和为 ,且满足 , , .(1)、求数列 的通项公式;(2)、若正项等比数列 满足 , ,且 ,数列 的前项和为 ,求证 .