湖北省黄冈市2018-2019学年高三上学期理数元月调研试卷
试卷更新日期:2019-03-18 类型:高考模拟
一、单选题
-
1. 复数 满足 ,则 的共轭复数 对应的点是第 象限的点A、一 B、二 C、三 D、四2. 已知函数 的定义域为 ,则 的定义域为A、
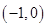 B、
B、 C、
C、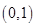 D、
D、 3. , ,若 ,则 的取值集合为A、
3. , ,若 ,则 的取值集合为A、 B、
B、 C、
C、 D、
D、 4. 过点 的直线在两坐标轴上的截距之和为零,则该直线方程为A、
4. 过点 的直线在两坐标轴上的截距之和为零,则该直线方程为A、 B、
B、 C、 或
C、 或  D、 或
D、 或  5. 下列有关命题的叙述错误的是A、命题“
5. 下列有关命题的叙述错误的是A、命题“ ,
,  ”的否定是“
”的否定是“  ,
,  ”
B、已知向量
”
B、已知向量  ,
,  ,则“
,则“  ”是“
”是“  ”的充分不必要条件
C、命题“若
”的充分不必要条件
C、命题“若  ,则
,则  的逆否命题为“若
的逆否命题为“若 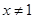 ,则
,则  ”
D、“
”
D、“  ”是
”是  的充分不必要条件
6. 已知角 的顶点与原点重合,始边与 轴的正半轴重合,终边在直线 上,则A、
的充分不必要条件
6. 已知角 的顶点与原点重合,始边与 轴的正半轴重合,终边在直线 上,则A、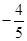 B、
B、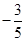 C、
D、
7. 已知圆 关于 对称,则 的值为A、 B、1 C、 D、08.A、
C、
D、
7. 已知圆 关于 对称,则 的值为A、 B、1 C、 D、08.A、 B、
C、
B、
C、 D、
9. 黄冈市有很多处风景名胜,仅 级景区就有10处,某单位为了鼓励职工好好工作,准备组织5名优秀的职工到就近的三个景区:龟峰山、天堂寨、红安红色景区去旅游,若规定每人限到一处旅游,且这三个风景区中每个风景区至少安排1人,则这5名职工共有 种安排方法A、90 B、60 C、210 D、15010. 函数 定义域为 ,若满足 在 内是单调函数; 存在 使 在 上的值域为 ,那么就称 为“半保值函数”,若函数 且 是“半保值函数”,则 的取值范围为A、
D、
9. 黄冈市有很多处风景名胜,仅 级景区就有10处,某单位为了鼓励职工好好工作,准备组织5名优秀的职工到就近的三个景区:龟峰山、天堂寨、红安红色景区去旅游,若规定每人限到一处旅游,且这三个风景区中每个风景区至少安排1人,则这5名职工共有 种安排方法A、90 B、60 C、210 D、15010. 函数 定义域为 ,若满足 在 内是单调函数; 存在 使 在 上的值域为 ,那么就称 为“半保值函数”,若函数 且 是“半保值函数”,则 的取值范围为A、 B、
B、 C、
C、 D、
D、 11. 关于圆周率 ,数学发展史上出现过许多有创意的求法,最著名的属普丰实验和查理实验受其启发,我们可以设计一个算法框图来估计 的值 如图 若电脑输出的 的值为29,那么可以估计 的值约为
11. 关于圆周率 ,数学发展史上出现过许多有创意的求法,最著名的属普丰实验和查理实验受其启发,我们可以设计一个算法框图来估计 的值 如图 若电脑输出的 的值为29,那么可以估计 的值约为 A、
A、 B、
B、 C、
C、 D、
D、 12. 已知圆 与函数 的图象有唯一交点,且交点的横坐标为 ,则 ( )A、 B、2 C、 D、3
12. 已知圆 与函数 的图象有唯一交点,且交点的横坐标为 ,则 ( )A、 B、2 C、 D、3二、填空题
-
13. 自2015年来黄冈市各重点高中开展了形式多样的各种选课走班活动,记者调查了黄梅一中甲、乙、丙三位同学,在被问到是否参加过黄梅戏、黄梅挑花、岳家拳这三个特长班时,甲说:我参加过的特长班比乙多,但没有参加过岳家拳;乙说:我没有参加过黄梅挑花;丙说:我们三个人都参加过同一个特长班,由此判断乙参加过的特长班为 .14. 正 中, 在 方向上的投影为 ,且 ,则 .15. 关于 的实系数方程 的一个根在 内,另一个根在 内,则 的值域为 .16. 意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:1,1,2,3,5,8,该数列的特点是:前两个数均为1,从第三个数起,每一个数都等于它前面两个数的和,人们把这样的一列数所组成的数列 称为“斐波那契数列”,则 .
三、解答题
-
17. 已知函数
 (1)、用“五点作图法”在给定的坐标系中,画出函数 在 上的图象.(2)、先将函数 的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数 的图象,求 的对称中心.18. 设 , 或 , ; 函数 在 上为增函数,若 ”为假,且“ ”为真,求实数 的取值范围.19. 黄冈市有很多名优土特产,黄冈市的蕲春县就有闻名于世的“蕲春四宝” 蕲竹、蕲艾、蕲蛇、蕲龟 ,很多人慕名而来旅游,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:
(1)、用“五点作图法”在给定的坐标系中,画出函数 在 上的图象.(2)、先将函数 的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数 的图象,求 的对称中心.18. 设 , 或 , ; 函数 在 上为增函数,若 ”为假,且“ ”为真,求实数 的取值范围.19. 黄冈市有很多名优土特产,黄冈市的蕲春县就有闻名于世的“蕲春四宝” 蕲竹、蕲艾、蕲蛇、蕲龟 ,很多人慕名而来旅游,通过随机询问60名不同性别的游客在购买“蕲春四宝”时是否在来蕲春县之前就知道“蕲春四宝”,得到如下列联表:男
女
总计
事先知道“蕲春四宝”
8
事先不知道“蕲春四宝”
4
36
总计
40
附:
(1)、写出列联表中各字母代表的数字;(2)、由以上列联表判断,能否在犯错误的概率不超过 的前提下认为购买“蕲春四宝”和是否“事先知道 蕲春四宝 有关系”?(3)、从被询问的 名事先知道“蕲春四宝”的顾客中随机选取2名顾客,求抽到的女顾客人数的分布列及其数学期望.