广东省茂名市2018-2019学年高三理数第一次综合测试试卷
试卷更新日期:2019-03-18 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 已知 是虚数单位,若 为实数,则实数 的值为( )A、1 B、-2 C、-1 D、03. 已知 , , ,则 的大小关系为( )A、
2. 已知 是虚数单位,若 为实数,则实数 的值为( )A、1 B、-2 C、-1 D、03. 已知 , , ,则 的大小关系为( )A、 B、
B、 C、
C、 D、
D、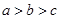 4. 七巧板是我国古代劳动人民发明的一种智力玩具,它是由五块等腰直角三角形、三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自黑色部分的概率为( )
4. 七巧板是我国古代劳动人民发明的一种智力玩具,它是由五块等腰直角三角形、三角形、一块正方形和一块平行四边形共七块板组成的.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自黑色部分的概率为( )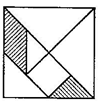 A、 B、 C、 D、
A、 B、 C、 D、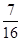 5. “ ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 已知函数 为偶函数,则a=( )A、1 B、2 C、 D、37. 函数 在 的图象大致是( )A、
5. “ ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件6. 已知函数 为偶函数,则a=( )A、1 B、2 C、 D、37. 函数 在 的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 已知函数 ,把 的图象向左平移 个单位得到函数 的图象,则下列说法正确的是( )A、
8. 已知函数 ,把 的图象向左平移 个单位得到函数 的图象,则下列说法正确的是( )A、 B、
B、 的图像关于直线
的图像关于直线  对称
C、
对称
C、 的一个零点为
的一个零点为  D、
D、 的一个单调减区间为
的一个单调减区间为  9. 如图,网格纸的正方形的边长是1,在其上用粗线画出了某多面体的三视图,则此几何体的体积为( )
9. 如图,网格纸的正方形的边长是1,在其上用粗线画出了某多面体的三视图,则此几何体的体积为( ) A、6 B、18 C、12 D、3610. 已知函数 是定义域在 上的偶函数,且 ,当 时, ,则关于 的方程 在 上所有实数解之和为( )A、1 B、3 C、6 D、711. 已知双曲线 的左,右焦点分别为 ,右顶点为 , 为其右支上一点, 与 渐近线交于点 ,与渐近线 交于点 , 的中点为 ,若 ,且 ,则双曲线的离心率为( )A、
A、6 B、18 C、12 D、3610. 已知函数 是定义域在 上的偶函数,且 ,当 时, ,则关于 的方程 在 上所有实数解之和为( )A、1 B、3 C、6 D、711. 已知双曲线 的左,右焦点分别为 ,右顶点为 , 为其右支上一点, 与 渐近线交于点 ,与渐近线 交于点 , 的中点为 ,若 ,且 ,则双曲线的离心率为( )A、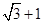 B、2
C、
D、
B、2
C、
D、
二、填空题
-
12. 已知向量 , ,若 ,则 .13. 的展开式中的常数项是 .14. 在 中,角 所对的边分别为 ,已知 , ,若 ,则 的面积为 .15. 把三个半径都是2的球放在桌面上,使它们两两相切,然后在它们上面放上第四个球(半径是2),使它与下面的三个球都相切,则第四个球的最高点与桌面的距离为 .
三、解答题
-
16. 已知 为数列 的前 项和, .(1)、求数列 的通项公式.(2)、若 , ,求数列 的前 项和 .17. 2018年茂名市举办“好心杯”少年美术书法作品比赛,某赛区收到200件参赛作品,为了解作品质量,现从这些作品中随机抽取12件作品进行试评.成绩如下:67,82,78,86,96,81,73,84,76,59,85,93.(1)、求该样本的中位数和方差;(2)、若把成绩不低于85分(含85分)的作品认为为优秀作品,现在从这12件作品中任意抽取3件,求抽到优秀作品的件数的分布列和期望.
18. 已知在三棱锥 中, , . (1)、求证: ;(2)、若 , ,求二面角 的平面角的余弦值.19. 已知抛物线 ,点 与抛物线 的焦点 关于原点对称,动点 到点 的距离与到点 的距离之和为4.(1)、求动点 的轨迹;(2)、若 ,设过点 的直线 与 的轨迹相交于 两点,当 的面积最大时,求直线 的方程.
(1)、求证: ;(2)、若 , ,求二面角 的平面角的余弦值.19. 已知抛物线 ,点 与抛物线 的焦点 关于原点对称,动点 到点 的距离与到点 的距离之和为4.(1)、求动点 的轨迹;(2)、若 ,设过点 的直线 与 的轨迹相交于 两点,当 的面积最大时,求直线 的方程.